Bài 94 trang 140 Sách bài tập Hình học lớp 12 Nâng cao

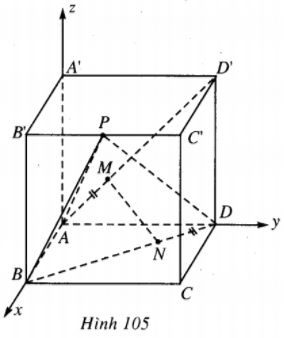
Cho hình lập phương ABCD.A^’B^’C^’D^’ cạnh bằng a. Xét hai điểm M trên AD’ và N trên DB sao cho  AM= DN= k (0< k <a\(\sqrt 2 \) ). Gọi P là trung điểm B’C’.

a) Tính cos của góc giữa hai đường thẳng AP và BC’.

b) Tính thể tích khối tứ diện APBC’.

c) Chứng minh MN luôn song song với mặt phẳng (A’D’CB) khi k thay đổi.

d) Tìm k để đoạn MN ngắn nhất.

e) Khi đoạn MN ngắn nhất, chứng minh rằng MN là đường vuông góc chung của AD’ và DB, đồng thời MN song song với A’C.

Giải

Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA' (h.105).

Khi đó :

         \(\eqalign{  & A = \left( {0;0;0} \right)  \cr  & B = \left( {a;0;0} \right)  \cr  & D = \left( {0;a;0} \right)  \cr  & C = \left( {a;a;0} \right) \cr} \)  \(\eqalign{  & A' = \left( {0;0;a} \right)  \cr  & B' = \left( {a;0;a} \right)  \cr  & D' = \left( {0;a;a} \right)  \cr  & C' = \left( {a;a;a} \right) \cr} \)

          \(P = \left( {a;{a \over 2};a} \right)\)

a) Ta có \(\overrightarrow {AP}  = \left( {a;{a \over 2};a} \right)\)

                       \(\overrightarrow {BC'}  = \left( {0;a;a} \right).\)

Gọi \(\alpha \) là góc giữa hai đường thẳng \(AP\) và \(BC'\) ta có :

         \(\cos \alpha  = {{\left| {0 + {{{a^2}} \over 2} + {a^2}} \right|} \over {\sqrt {{a^2} + {{{a^2}} \over 2} + {a^2}} .\sqrt {{a^2} + {a^2}} }} = {1 \over {\sqrt 2 }} \Rightarrow \alpha  = {45^o}\)

b) Ta có : \(\overrightarrow {AP}  = \left( {a;{a \over 2};a} \right)\), \(\overrightarrow {AB}  = {\rm{ }}\left( {a;0;0} \right),\overrightarrow {AC'}  = (a;a;a)\)

\(\eqalign{  &  \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right] = \left( {\left| {\matrix{   {{a \over 2}} & a  \cr   0 & 0  \cr  } } \right|;\left| {\matrix{   a & a  \cr   0 & a  \cr  } } \right|;\left| {\matrix{   a & {{a \over 2}}  \cr   a & 0  \cr  } } \right|} \right) \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \left( {0;{a^2}; - {{{a^2}} \over 2}} \right)  \cr  &  \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'}  = 0 + {a^3} - {{{a^3}} \over 2} = {{{a^3}} \over 2}. \cr} \)

Vậy \({V_{APBC'}} = {1 \over 6}\left| {\left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'} } \right| = {1 \over 6}.{{{a^3}} \over 2} = {{{a^3}} \over {12}}.\) 

c) Mặt phẳng \(\left( {A'D'CB} \right)\) song song với trục Oy nên có phương trình :

       \(px{\rm{ }} + {\rm{ }}qz{\rm{ }} + {\rm{ }}n{\rm{ }} = 0\) \(\left( {n \ne 0,{p^2} + {q^2} > 0} \right).\)

Vì mặt phẳng này đi qua \(A',B,C\) nên ta xác định được p = q và n = -pa.

Cho p = 1, ta được phương trình mp\(\left( {A'D'CB} \right)\) là \(x + z - {\rm{ }}a = {\rm{ }}0\). Vectơ pháp tuyến của mặt phẳng này là \(\overrightarrow n  = {\rm{ }}\left( {1{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}1} \right).\)

Từ giả thiết \(M \in AD',{\rm{ }}N \in DB;{\rm{ }}AM = {\rm{ }}DN = k\), ta tính được :

                      \(M = \left( {0;{k \over {\sqrt 2 }};{k \over {\sqrt 2 }}} \right),N = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -k} \over {\sqrt 2 }};0} \right).\)

Suy ra \(\overrightarrow {MN}  = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -2k} \over {\sqrt 2 }}; - {k \over {\sqrt 2 }}} \right).\)

Ta có \(\overrightarrow {MN} .\overrightarrow n  = 1.{k \over {\sqrt 2 }} + 0\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right) + 1.\left( { - {k \over {\sqrt 2 }}} \right) = 0\)

\(\Rightarrow \overrightarrow {MN}  \bot \overrightarrow n .\)

Rõ ràng \(N \notin mp\left( {A'D'CB} \right).\) Suy ra MN song song với mp\(\left( {A'D'CB} \right).\)

d) Ta có \(M{N^2} = {\left( {{k \over {\sqrt 2 }}} \right)^2} + {\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right)^2} + {\left( { - {k \over {\sqrt 2 }}} \right)^2}.\)

\(\eqalign{  &  = 3{k^2} - 2a\sqrt 2 k + {a^2}  \cr  &  = 3\left[ {{{\left( {k - {{a\sqrt 2 } \over 3}} \right)}^2} + {{{a^2}} \over 9}} \right] \ge 3{{{a^2}} \over 9} = {{{a^2}} \over 3}. \cr} \)

\(M{N^2}\) nhỏ nhất bằng \({{{a^2}} \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\) (thoả mãn điều kiện \(0{\rm{ }} < k{\rm{ }} < {\rm{ }}a\sqrt 2 \) ).

Vậy MN ngắn nhất bằng \({{a\sqrt 3 } \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\).

e) Khi MN ngắn nhất thì \(k = {{a\sqrt 2 } \over 3}\) Khi đó \(\overrightarrow {MN}  = \left( {{a \over 3};{a \over 3};{{ - a} \over 3}} \right).\)

Ta lại có \(\overrightarrow {AD'}  = {\rm{ }}\left( {0;a;{\rm{ }}a} \right),\overrightarrow {DB} {\rm{ }} = (a; - a;0)\) nên \(\overrightarrow {MN} .\overrightarrow {AD'}  = {\rm{ }}0,\overrightarrow {MN} .\overrightarrow {DB}  = {\rm{ }}0.\)

Vậy MN là đường vuông góc chung của AD' và DB.

Mặt khác \(\overrightarrow {A'C}  = \left( a;a; - a\right) = 3\overrightarrow {MN} \), chứng tỏ \(\overrightarrow {MN} \), \(\overrightarrow {A'C} \) cùng phương. Do \(N \not\in A'C\)  nên \(MN//A'C.\)

Sachbaitap.com