Giải SGK Toán 11 Cánh Diều tập 2 trang 88

Bài 1 trang 88 SGK Toán 11 - Cánh Diều tập 2

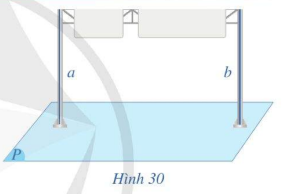
Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng.

Phương pháp:

Dựa vào tính chất đã học để xác định.

Lời giải:

Quan sát Hình 30 ta thấy a // b, a và b cùng vuông góc với (P). Qua đó, một số các tính chất về quan hệ vuông góc giữa đường thẳng và mặt phẳng được gợi ra như sau:

⦁ Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

⦁ Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.

Bài 2 trang 88 SGK Toán 11 - Cánh Diều tập 2

Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).

a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC)

b) Giả sử \(BC \bot SA, CA \bot SB\). Chứng minh rằng H là trực tâm của tam giác ABC và \(AB \bot SC\)

Phương pháp:

Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với 2 đường thẳng cắt nhau nằm trong mặt phẳng đó.

Lời giải:

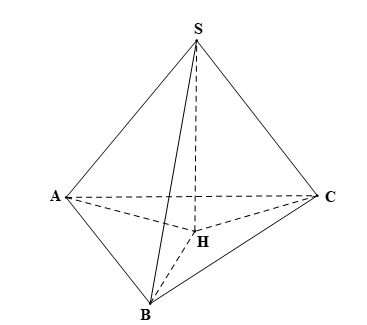
a) Ta có: H là hình chiếu của S trên mặt phẳng (ABC); A ∈ (ABC).

Suy ra HA là hình chiếu của SA trên mặt phẳng (ABC).

Tương tự ta có HB, HC lần lượt là hình chiếu của SB và SC trên mặt phẳng (ABC).

b) Do H là hình chiếu của S trên mặt phẳng (ABC) nên SH ⊥ (ABC).

Mà AB, AC, BC đều nằm trên (ABC).

Từ đó ta có: SH ⊥ AB, SH ⊥ AC, SH ⊥ BC.

· Ta có: BC ⊥ SH, BC ⊥ SA và SH ∩ SA = S trong (SAH).

Suy ra BC ⊥ (SAH).

Mà AH ⊂ (SAH) nên BC ⊥ AH. (1)

· Ta có: AC ⊥ SB, AC ⊥ SH và SB ∩ SH = S trong (SBH).

Suy ra AC ⊥ (SBH).

Mà BH ⊂ (SBH) nên AC ⊥ BH. (2)

Từ (1) và (2) ta có H là trực tâm của tam giác ABC.

Suy ra AB ⊥ CH.

· Ta có: AB ⊥ CH, AB ⊥ SH và CH ∩ SH = H trong (SCH).

Suy ra AB ⊥ (SCH).

Mà SC ⊂ (SCH) nên AB ⊥ SC.

Bài 3 trang 88 SGK Toán 11 - Cánh Diều tập 2

Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:

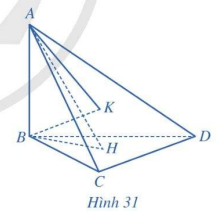
a)\(CD \bot (ABH)\)

b)\(CD \bot (ABK)\)

c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm.

Phương pháp:

Dựa vào điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh.

Lời giải:

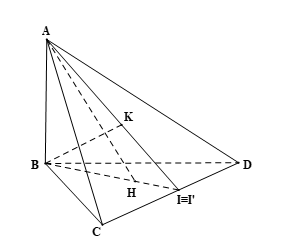
a) Ta có: AB ⊥ (BCD), CD ⊂ (BCD) nên AB ⊥ CD.

Do H là trực tâm của tam giác BCD nên BH ⊥ CD.

Ta có: CD ⊥ AB, CD ⊥ BH và AB ∩ BH = B trong (ABH).

Từ đó ta có: CD ⊥ (ABH).

b) Do K là trực tâm của tam giác ACD nên AK ⊥ CD.

Ta có: CD ⊥ AB, CD ⊥ AK và AB ∩ AK = A trong (ABK).

Từ đó ta có: CD ⊥ (ABK).

c) Theo tính chất “Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước” nên có duy nhất một mặt phẳng đi qua điểm A và vuông góc với CD.

Mà CD ⊥ (ABH), CD ⊥ (ABK).

Suy ra (ABH) ≡ (ABK).

Do: -  H là trực tâm của tam giác BCD nên BH giao với CD tại một điểm I;

       -  K là trực tâm của tam giác ACD nên AK giao với CD tại một điểm I’.

Mà CD cắt (ABHK) tại một điểm.

Do đó I và I’ trùng nhau hay AK, BH, CD cùng đi qua một điểm.

Bài 4 trang 88 SGK Toán 11 - Cánh Diều tập 2

Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng: 

a) SA \(\bot\) AD;

b) SC \(\bot\) CD.

Phương pháp:

Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh.

Lời giải:

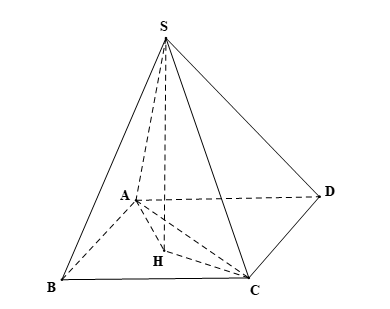
a) Ta có H là trực tâm của tam giác ABC nên AH ⊥ BC.

Hơn nữa BC // AD (do ABCD là hình bình hành).

Suy ra AH ⊥ AD.

Lại có H là hình chiếu của S trên (ABCD) nên HA là hình chiếu của SA trên (ABCD).

Do đó, theo định lí ba đường vuông góc ta có AD ⊥ SA hay SA ⊥ AD.

b) Ta có H là trực tâm của tam giác ABC nên CH ⊥ AB.

Hơn nữa AB // CD (do ABCD là hình bình hành).

Suy ra HC ⊥ CD.

Lại có H là hình chiếu của S trên (ABCD) nên HC là hình chiếu của SC trên (ABCD).

Do đó, theo định lí ba đường vuông góc ta có CD ⊥ SC hay SC ⊥ CD.

Bài 5 trang 88 SGK Toán 11 - Cánh Diều tập 2

Cho hình chóp S.ABCD có SA \(\bot\) (ABC), BC \(\bot\) AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông.

Phương pháp:

Dựa vào định lí vừa học để chứng minh.

Lời giải:

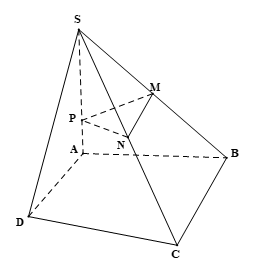
Do SA ⊥ (ABC) hay SA ⊥ (ABCD) nên AB là hình chiếu của SB trên mặt phẳng (ABCD).

Mà BC ⊥ AB nên theo định lí ba đường vuông góc ta có BC ⊥ SB.

Xét ∆SBC có: M, N lần lượt là trung điểm của SB và SC nên MN là đường trung bình của ∆SBC. Do đó MN // BC.

Mà BC ⊥ SB nên SB ⊥ MN.

Do SA ⊥ (ABCD) và BC ⊂ (ABCD) suy ra SA ⊥ BC.

Mà MN // BC nên SA ⊥ MN.

Ta có: MN ⊥ SB, MN ⊥ SA và SB ∩ SA = S trong (SAB).

Suy ra MN ⊥ (SAB).

Hơn nữa PM ⊂ (SAB) nên MN ⊥ PM hay tam giác MNP là tam giác vuông tại M.

Sachbaitap.com