Giải SGK Toán 12 tập 1 Cánh Diều trang 42, 43, 44
Giải bài 1, 2 trang 42 bài 2, 3, 4, 5, 6 trang 43 bài 7, 8 trang 44 SGK Toán 12 Cánh Diều tập 1. Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm.
Bài 1 trang 42 SGK Toán 12 Tập 1 Cánh Diều
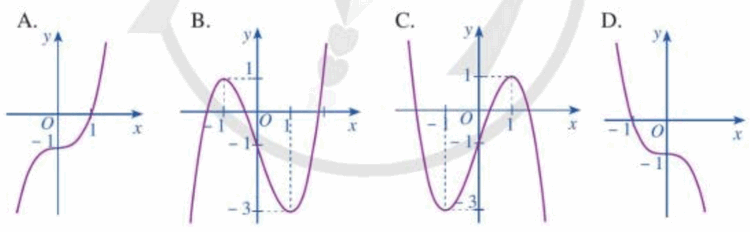
Đồ thị hàm số \(y = {x^3} - 3x - 1\) là đường cong sau ?
Phương pháp:
+, Tìm tập xác định hàm số
+, Xét sự biến thiên
+, xét hàm số
Lời giải:
Đáp án đúng là: B
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = 3x2 – 3;
y' = 0 ⇔ x = – 1 hoặc x = 1.
Bảng biến thiên của hàm số là
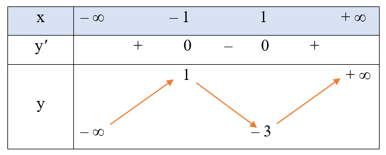
Do đó, đồ thị của hàm số y = x3 – 3x – 1 là
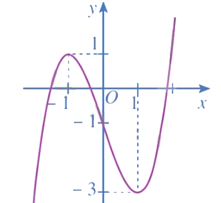
Bài 2 trang 42 SGK Toán 12 Tập 1 Cánh Diều

Phương pháp:
+, Xét đồng biến nghịch biến của hàm số
+, Tìm giao điểm trục tung và trục hoành
+, Xét hàm số
Lời giải:
Đáp án đúng là: D
Ta thấy đồ thị hàm số đi lên từ trái qua phải nên loại đáp án B.
Đồ thị hàm số đi qua điểm (– 2; – 2) nên thay vào các đáp án ta loại được đáp án A và đáp án C. Vậy đường cong trong Hình 29 là đồ thị hàm số ở đáp án D.
Bài 3 trang 43 SGK Toán 12 Tập 1 Cánh Diều
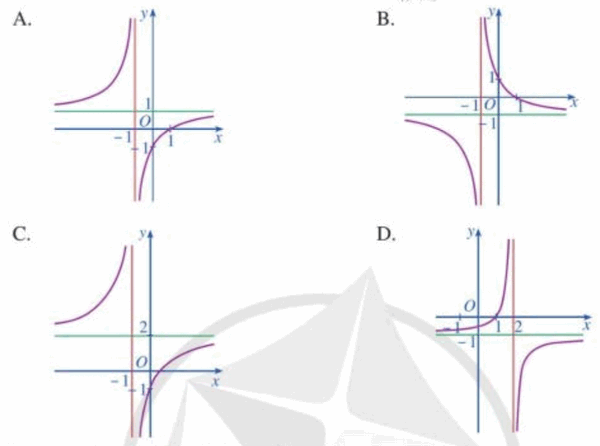
Đường cong nào sau đây là đò thị của hàm số \(y = \frac{{1 - x}}{{x + 1}}\) ?
Phương pháp:
Tìm tập xác định.
Xác định tiệm cận đứng tiệm cận ngang của hàm số.
Lời giải:
Đáp án đúng là: B
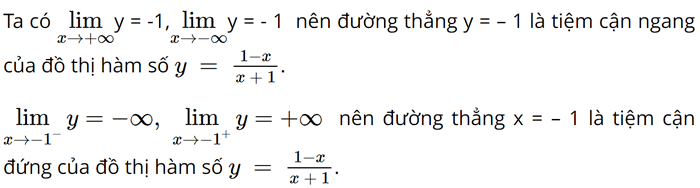
Vậy đường cong trong đáp án B là đồ thị của hàm số đã cho.
Bài 4 trang 43 SGK Toán 12 Tập 1 Cánh Diều
Phương pháp:
Xét tiệm cận xiên của đồ thị.
Xét các hàm số.
Lời giải:
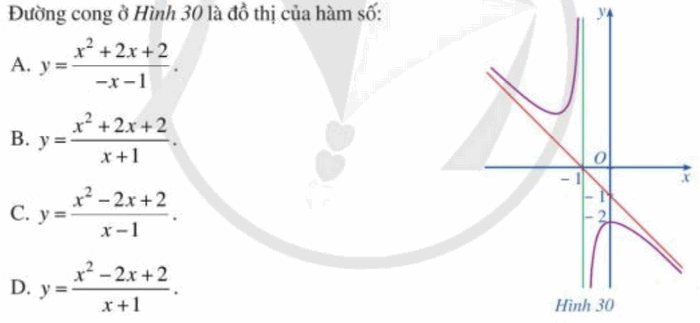
Đáp án đúng là: A
Đồ thị hàm số trong Hình 30 cắt trục tung tại điểm (0; – 2) và có tiệm cận đứng là đường thẳng x = – 1 và tiệm cận xiên là đường thẳng y = – x – 1.
Thay tọa độ điểm (0; – 2) vào các hàm số ở các đáp án ta loại được đáp án B và D.
Ta thấy đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số 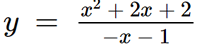 và đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số
và đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số 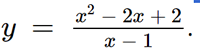
Vậy đường cong trong Hình 30 là đồ thị của hàm số 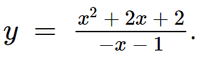
Bài 5 trang 43 SGK Toán 12 Tập 1 Cánh Diều
khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau:
a,\(y = 2{x^3} - 3x + 1\)
b,\(y = - {x^3} + 3x - 1\)
c, \( y = {\left( {x - 2} \right)^3} + 4\)
d,\(y = - {x^3} + 3{x^2} - 1\)
e, \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1\)
g,\( y = - {x^3} - 3x\)
Phương pháp:
Tìm TXD.
Xét sự biến thiên.
Vẽ đồ thị.
Lời giải:
a) y = 2x3 – 3x2 + 1
1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 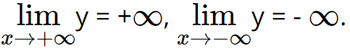
• y' = 6x2 – 6x;
y' = 0 ⇔ 6x2 – 6x = 0 ⇔ x = 0 hoặc x = 1.
• Bảng biến thiên:
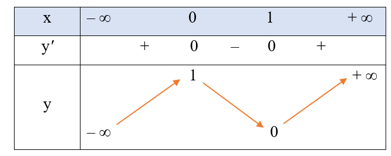
Hàm số đã cho đồng biến trên mỗi khoảng (– ∞; 0) và (1; + ∞); nghịch biến trên khoảng (0; 1).
Hàm số đạt cực đại tại x = 0, yCĐ = 1; đạt cực tiểu tại x = 1, yCT = 0.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; 1).
• Giao điểm của đồ thị với trục hoành:
Giải phương trình 2x3 – 3x2 + 1 = 0 ta được 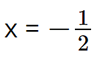 hoặc x = 1.
hoặc x = 1.
Vậy đồ thị hàm số giao với trục hoành tại các điểm 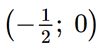 , (1; 0).
, (1; 0).
• Đồ thị hàm số đi qua các điểm (1; 0), (0; 1), 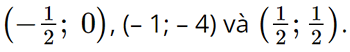
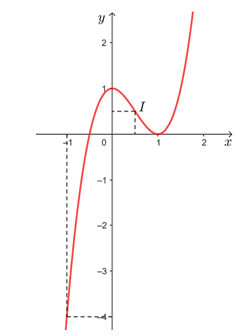
Vậy đồ thị hàm số y = 2x3 – 3x2 + 1 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm 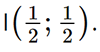
b) y = – x3 + 3x2 – 1
1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 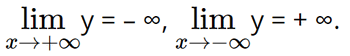
• y' = – 3x2 + 6x;
y' = 0 ⇔ – 3x2 + 6x = 0 ⇔ x = 0 hoặc x = 2.
• Bảng biến thiên:
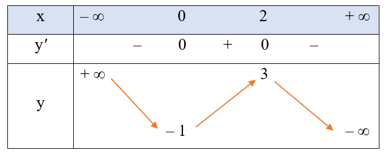
Hàm số đã cho đồng biến trên khoảng (0; 2); nghịch biến trên mỗi khoảng (– ∞; 0) và (2; + ∞).
Hàm số đạt cực đại tại x = 2, yCĐ = 3; đạt cực tiểu tại x = 0, yCT = – 1.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 1).
• Giao điểm của đồ thị với trục hoành:
Giải phương trình – x3 + 3x2 – 1 = 0, ta thấy phương trình có 3 nghiệm phân biệt nên đồ thị hàm số cắt trục hoành tại 3 điểm.
• Đồ thị hàm số đi qua các điểm (– 1; 3), (0; – 1), (1; 1), (2; 3) và (3; – 1).
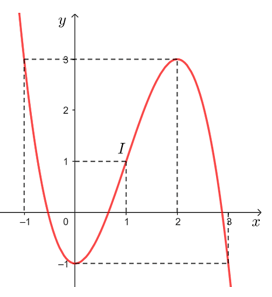
Vậy đồ thị hàm số y = – x3 + 3x2 – 1 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(1; 1).
c) Ta có y = (x – 2)3 + 4 = x3 – 6x2 + 12x – 8 + 4 = x3 – 6x2 + 12x – 4.
1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 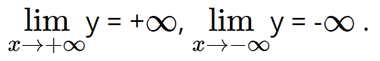
• y' = 3x2 – 12x + 12 = 3(x – 2)2;
y' ≥ 0 với mọi x ∈ ℝ.
y' = 0 khi x = 2.
• Bảng biến thiên:
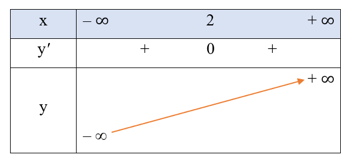
Hàm số đồng biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 4).
• Giao điểm của đồ thị với trục hoành:
Giải phương trình x3 – 6x2 + 12x – 4 = 0, ta thấy phương trình có 1 nghiệm nên đồ thị hàm số cắt trục hoành tại 1 điểm.
• Đồ thị hàm số đi qua các điểm (0; – 4), (1; 3), (2; 4) và (3; 5).
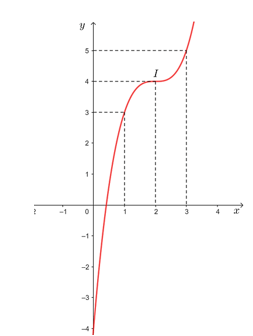
Vậy đồ thị hàm số y = (x – 2)3 + 4 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(2; 4).
d) y = – x3 + 3x2 – 3x + 2
1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 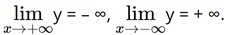
• y' = – 3x2 + 6x – 3 = – 3(x – 1)2 ≤ 0 với mọi x ∈ ℝ;
y' = 0 khi x = 1.
• Bảng biến thiên:
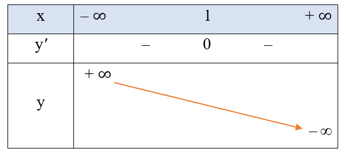
Hàm số đã cho nghịch biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; 2).
• Giao điểm của đồ thị với trục hoành:
Giải phương trình – x3 + 3x2 – 3x + 2 = 0 ta được x = 2.
Vậy đồ thị hàm số cắt trục hoành tại điểm (2; 0).
• Đồ thị hàm số đi qua các điểm (0; 2), (2; 0) và (1; 1).
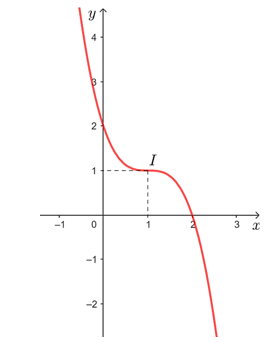
Vậy đồ thị hàm số y = – x3 + 3x2 – 3x + 2 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(1; 1).

1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 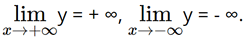
• y' = x2 + 2x + 2 = (x + 1)2 + 1 > 0 với mọi x ∈ ℝ;
• Bảng biến thiên:
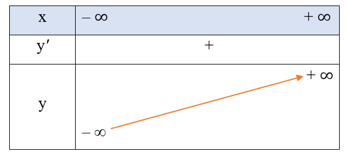
Hàm số đã cho đồng biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; 1).
• Giao điểm của đồ thị với trục hoành:
Giải phương trình 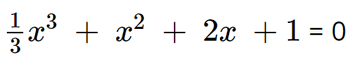 ta thấy có 1 nghiệm nên đồ thị hàm số cắt trục hoành tại 1 điểm.
ta thấy có 1 nghiệm nên đồ thị hàm số cắt trục hoành tại 1 điểm.
• Đồ thị hàm số đi qua các điểm (0; 1), 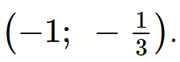
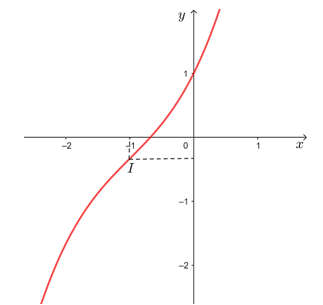
Vậy đồ thị hàm số 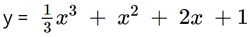 được cho như hình vẽ trên.
được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm 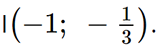
g) y = – x3 – 3x
1) Tập xác định: ℝ.
2) Sự biến thiên:
• Giới hạn tại vô cực: 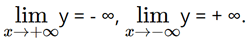
• y' = – 3x2 – 3 = – 3(x2 + 1) < 0 với mọi x ∈ ℝ;
• Bảng biến thiên:
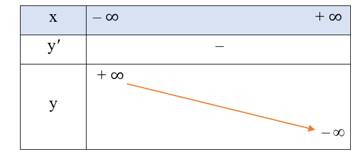
Hàm số đã cho nghịch biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
• Đồ thị hàm số đi qua các điểm (0; 0), (– 1; 4) và (1; – 4).
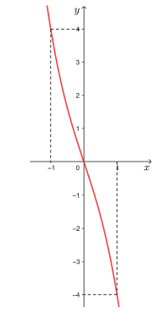
Vậy đồ thị hàm số y = – x3 – 3x được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm O(0; 0).
Bài 6 trang 43 SGK Toán 12 Tập 1 Cánh Diều
Khảo sát sự biến thiên của các hàm số sau:
a, \(y = \frac{{x - 1}}{{x + 1}}\)
b,\(y = \frac{{ - 2x}}{{x + 1}}\)
c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\)
d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)
e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)
g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Lời giải:
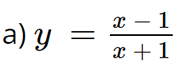
1) Tập xác định: ℝ \ {– 1}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

• Bảng biến thiên:
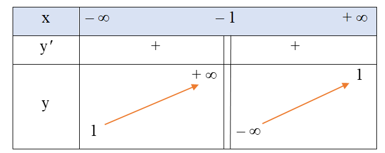
Hàm số đồng biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 1).
• Giao điểm của đồ thị với trục hoành: (1; 0).
• Đồ thị hàm số đi qua các điểm (0; – 1), (1; 0), (– 2; 3) và (– 3; 2).
• Đồ thị hàm số nhận giao điểm I(– 1; 1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
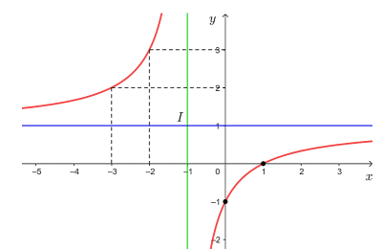
Vậy đồ thị hàm số 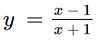 được cho ở hình trên.
được cho ở hình trên.
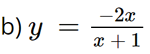
1) Tập xác định: ℝ \ {– 1}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
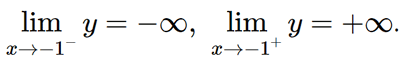 Do đó, đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
Do đó, đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
Bảng biến thiên:
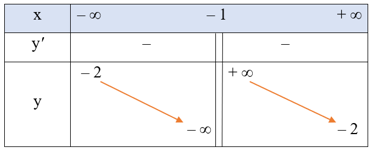
Hàm số nghịch biến trên mỗi khoảng (– ∞; – 1) và (– 1; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
• Đồ thị hàm số đi qua các điểm (– 3; – 3), (– 2; – 4), (0; 0) và (1; – 1).
• Đồ thị hàm số nhận giao điểm I(– 1; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
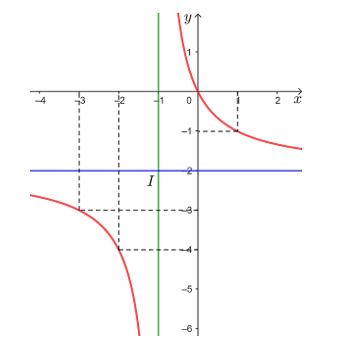
Vậy đồ thị hàm số 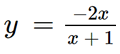 được cho ở hình trên.
được cho ở hình trên.
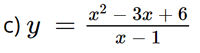
1) Tập xác định: ℝ \ {1}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

y' = 0 ⇔ x2 – 2x – 3 = 0 ⇔ x = – 1 hoặc x = 3.
• Bảng biến thiên:
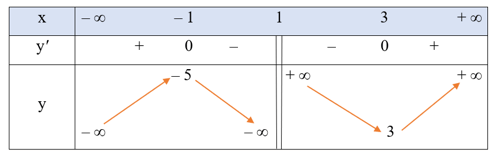
Hàm số đồng biến trên mỗi khoảng (– ∞; – 1) và (3; + ∞); nghịch biến trên mỗi khoảng (– 1; 1) và (1; 3).
Hàm số đạt cực đại tại x = – 1, yCĐ = – 5; đạt cực tiểu tại x = 3, yCT = 3.
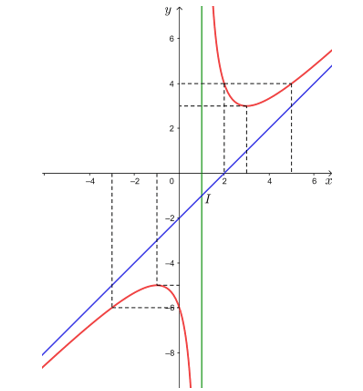
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; – 6).
• Đồ thị hàm số không cắt trục hoành.
• Đồ thị hàm số đi qua các điểm (– 3; – 6), (– 1; – 5), (0; – 6), (2; 4), (3; 3) và (5; 4).
• Đồ thị hàm số nhận giao điểm I(1; – 1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
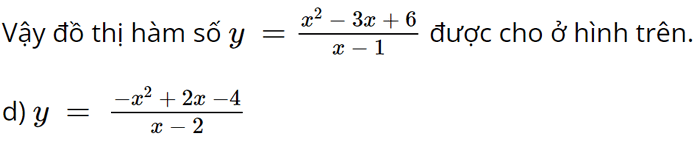
1) Tập xác định: ℝ \ {2}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:

y' = 0 ⇔ – x2 + 4x = 0 ⇔ x = 0 hoặc x = 4.
• Bảng biến thiên:
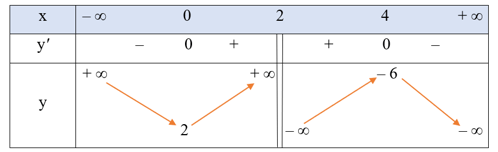
Hàm số đã cho đồng biến trên mỗi khoảng (0; 2) và (2; 4); nghịch biến trên mỗi khoảng (– ∞; 0) và (4; + ∞).
Hàm số đạt cực đại tại x = 4, yCĐ = – 6; đạt cực tiểu tại x = 0, yCT = 2.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: (0; 2).
• Đồ thị hàm số không cắt trục hoành.
• Đồ thị hàm số đi qua các điểm (– 2; 3), (0; 2), (1; 3), (3; – 7), (4; – 6) và (6; – 7).
• Đồ thị hàm số nhận giao điểm I(2; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
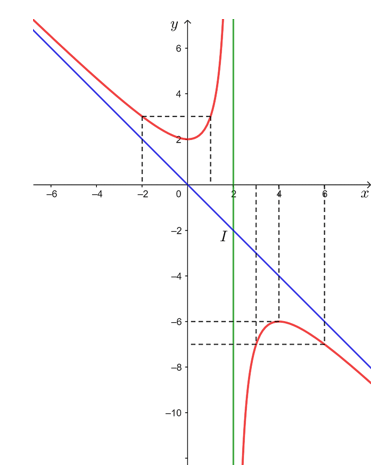
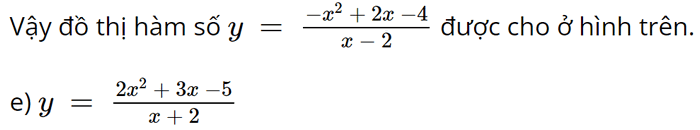
1) Tập xác định: ℝ \ {– 2}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
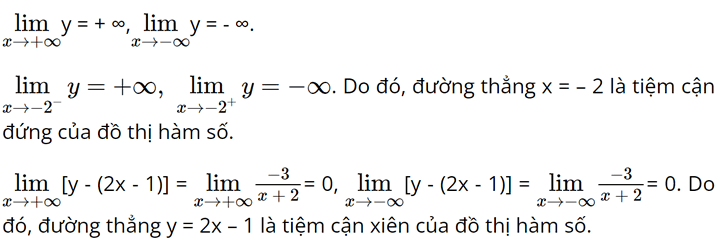
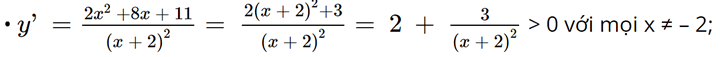
• Bảng biến thiên:
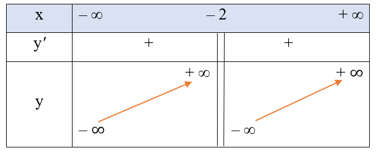
Hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (– 2; + ∞).
Hàm số không có cực trị.
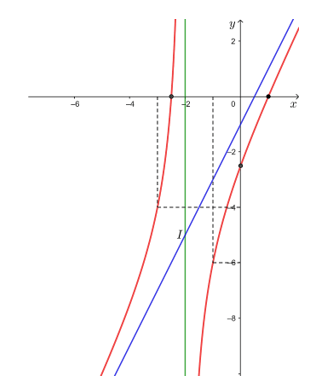
3) Đồ thị

• Đồ thị hàm số nhận giao điểm I(– 2; – 5) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
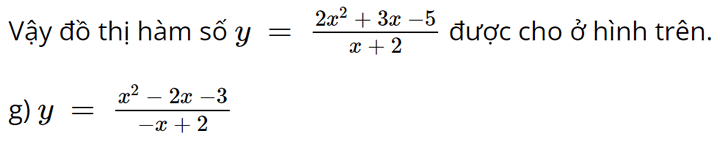
1) Tập xác định: ℝ \ {2}.
2) Sự biến thiên
• Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
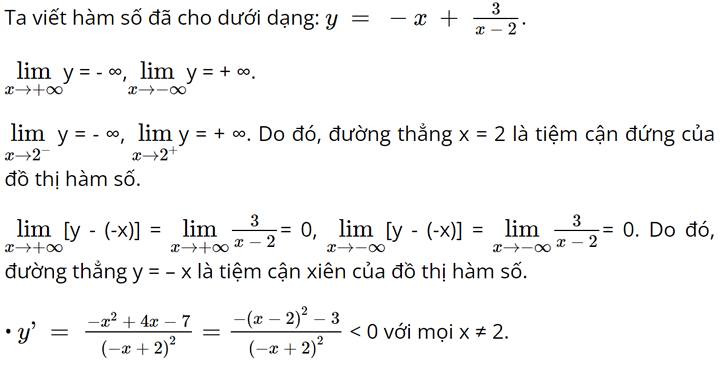
• Bảng biến thiên:
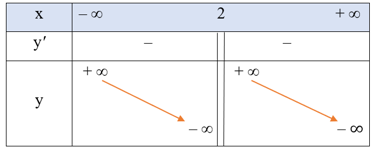
Hàm số đã cho nghịch biến trên mỗi khoảng (– ∞; 2) và (2; + ∞).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: 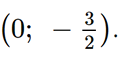
• Giao điểm của đồ thị với trục hoành:
Giải phương trình 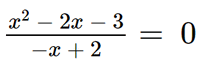 ta được x = – 1 và x = 3.
ta được x = – 1 và x = 3.
Vậy đồ thị hàm số cắt trục hoành tại hai điểm (– 1; 0) và (3; 0).
• Đồ thị hàm số đi qua các điểm (– 1; 0), 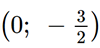 , (1; – 4), (3; 0) và (5; – 4).
, (1; – 4), (3; 0) và (5; – 4).
• Đồ thị hàm số nhận giao điểm I(2; – 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
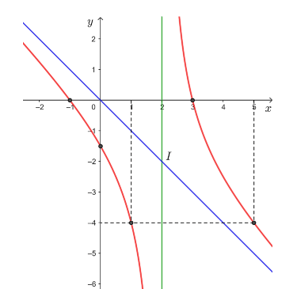
Vậy đồ thị hàm số 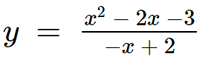 được cho ở hình trên.
được cho ở hình trên.
Bài 7 trang 44 SGK Toán 12 Tập 1 Cánh Diều
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng.
Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm.
\(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\)
Trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét
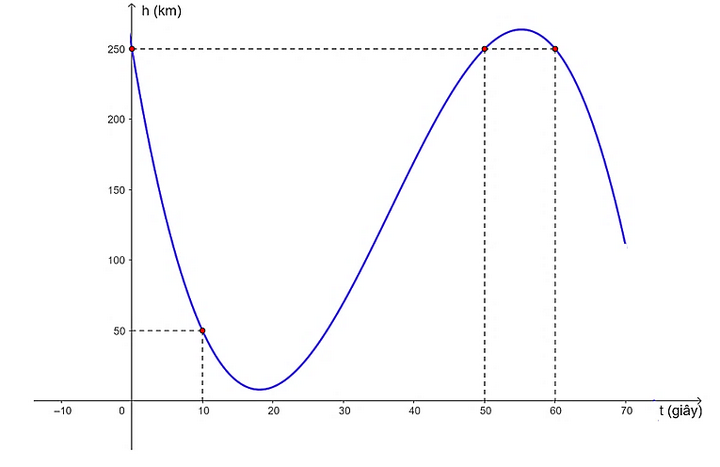
a) Vẽ đồ thị của hàm số \(y = h\left( t \right)\) với \(0{\rm{ }} \le t \le {\rm{ }}50\) (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 10 km).
b) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với \(0{\rm{ }} \le t \le {\rm{ }}50\). Xác định hàm số v(t).
c) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
d) Tại thời điểm t = 25 (giây), vận tốc của con tàu vẫn giảm hay tăng trở lại?
e) Tìm thời điểm t (\(0{\rm{ }} \le t \le {\rm{ }}50\)) Sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
Lời giải:
a) Xét hàm số h(t) = – 0,01t3 + 1,1t2 – 30t + 250 với t ∈ [0; 70].
Ta có h'(t) = – 0,03t2 + 2,2t – 30;
Trên khoảng (0; 70), h'(t) = 0 khi t ≈ 18 hoặc t ≈ 55.
h(0) = 250; h(18) ≈ 8,08; h(55,23) ≈ 263,75; h(70) = 110.
Do đó, 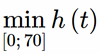 = 8,08 tại t = 18.
= 8,08 tại t = 18.
Vậy tại thời điểm t = 18 giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
b) Xét hàm số h(t) = – 0,01t3 + 1,1t2 – 30t + 250 với t ∈ [0; 70].
Ta có h'(t) = – 0,03t2 + 2,2t – 30;
Trên khoảng (0; 70), h'(t) = 0 khi t ≈ 18 hoặc t ≈ 55.
Bảng biến thiên của hàm số h(t) như sau:
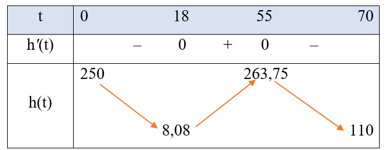
Trên khoảng (0; 70), đồ thị hàm số h(t) đi qua các điểm (0; 250), (10; 50), (50; 250) và (60; 250).
c) Ta có v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤ 70.
Khi đó v(t) = h'(t) = – 0,03t2 + 2,2t – 30 với t ∈ [0; 70].
d) Tại thời điểm bắt đầu đốt cháy các tên lửa hãm, tức t = 0, vận tốc của tức thời của con tàu là:
v(0) = – 0,03 ∙ 02 + 2,2 ∙ 0 – 30 = – 30 (km/s).
Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu là:
v(25) = – 0,03 ∙ 252 + 2,2 ∙ 25 – 30 = 6,25 (km/s).
e) Tại thời điểm t = 25 (giây), lúc đó t ∈ (18; 55), căn cứ vào bảng biến thiên ở câu b), ta thấy rằng h'(t) > 0, tức là v(t) > 0, vậy vận tốc tức thời của con tàu đang tăng trở lại.
Bài 8 trang 44 SGK Toán 12 Tập 1 Cánh Diều
Xét phản ứng hoá học tạo ra chất C từ hai chất A và B:
\(A{\rm{ }} + {\rm{ }}B{\rm{ }} \to {\rm{ }}C\)
Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: \(\left[ C \right]\; = \;\frac{{{a^2}Kt}}{{aKt + 1}}\) (mol/l), trong đó K là hằng số dương.
a) Tìm tốc độ phản ứng ở thời điểm t > 0.
b) Chứng minh nếu \(x\; = \;\left[ C \right]\) thì
c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t\; \to \; + \infty \)
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t\; \to \; + \infty \)
Lời giải:
a) Ta có
A + B → C
Ban đầu: a + a 0
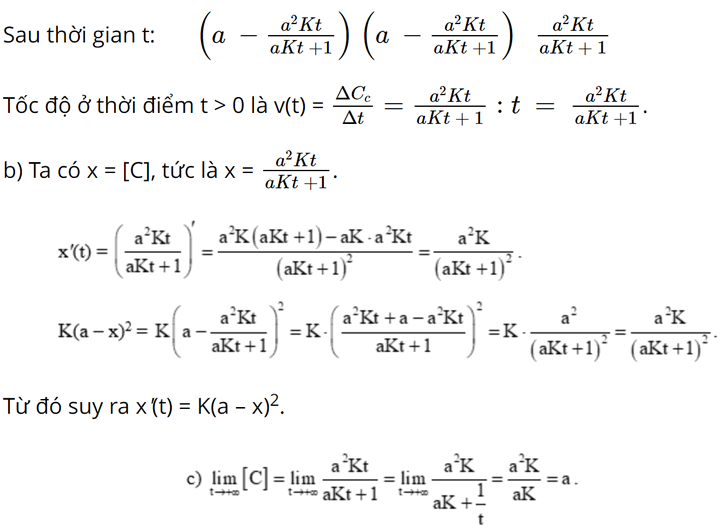
Vậy khi t → + ∞ thì nồng độ các chất A, B và C bằng nhau.
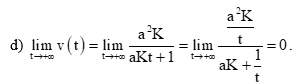
Vậy khi t → + ∞, tốc độ phản ứng dần về 0, khi đó phản ứng kết thúc.
Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 3
- Bài 2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
- Bài 1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
- CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO MẪU SỐ LIỆU GHÉP NHÓM
- Bài tập cuối chương 2
- Bài 3. Biểu thức toạ độ của các phép toán vectơ
- Bài 2. Toạ độ của vectơ
- Bài 1. Vectơ và các phép toán vectơ trong không gian
- CHƯƠNG II. TỌA ĐỘ VECTƠ TRONG KHÔNG GIAN
- Bài tập cuối chương 1
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
