Giải SGK Toán 12 tập 1 Cánh Diều trang 72, 73
Giải bài 1, 2, 3, 4 trang 72 bài 5, 6, 7, 8, 9 trang 73 SGK Toán 12 Cánh Diều tập 1. Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.
Bài 1 trang 72 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3). Tọa độ của vectơ OA là:
A. (1; 2; 3).
B. (1; 0; 3).
C. (0; 2; 3).
D. (1; 2; 0).
Lời giải:
Đáp án đúng là: A
Ta có A(1; 2; 3). Do đó, 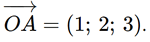
Bài 2 trang 72 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ Oxyz, cho vectơ 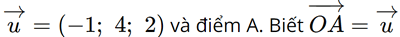 . Tọa độ của điểm A là:
. Tọa độ của điểm A là:
A. (1; 4; 2).
B. (– 1; 4; 2).
C. (1; – 4; – 2).
D. (– 1; – 4; – 2).
Lời giải:
Đáp án đúng là: B
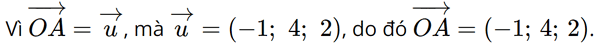
Từ đó suy ra A(– 1; 4; 2).
Bài 3 trang 72 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ Oxyz, cho vectơ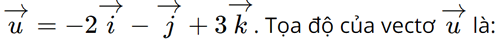
A. (– 2; – 1; 3).
B. (2; 1; 3).
C. (– 2; 0; 3).
D. (– 2; – 1; – 3).
Lời giải:
Đáp án đúng là: A
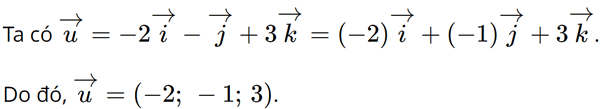
Bài 4 trang 72 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; – 1; 2) và B(4; – 3; 1). Tọa độ của vectơ AB là:
A. (– 3; 2; 1).
B. (3; – 2; – 1).
C. (5; – 4; 3).
D. (3; – 4; – 1).
Lời giải:
Đáp án đúng là: B
Với A(1; – 1; 2) và B(4; – 3; 1), ta có:
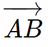 = (4 – 1; – 3 – (– 1); 1 – 2) = (3; – 2; – 1).
= (4 – 1; – 3 – (– 1); 1 – 2) = (3; – 2; – 1).
Bài 5 trang 72 SGK Toán 12 Tập 1 Cánh Diều
Số lượng sản phẩm bán được cho một công ty trong x (tháng) được tính theo công thức
\(S\left( x \right) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\) trong đó \(x \ge 1\).
a) Xem \(y = S\left( x \right)\) là một hàm số xác định trên nửa khoảng \([1; + \infty )\), hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.
Phương pháp:
a) Đường thẳng \(y = {y_o}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_o}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_o}\).
b) Dựa vào câu a) để kết luận
Lời giải:
Đáp án đúng là: C
Gọi tọa độ điểm C là (xC; yC; zC), ta có 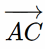 = (xC – 1; yC – 1; zC – 1).
= (xC – 1; yC – 1; zC – 1).
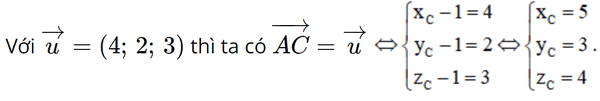
Vậy C(5; 3; 4).
Bài 6 trang 73 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( {3; - 2; - 1} \right)\). Gọi \({A_1},{A_2},{A_3}\) lần lượt là hình chiếu của điểm \(A\) trên các mặt phẳng tọa độ \(\left( {Oxy} \right),\left( {Oyz} \right),\left( {Ozx} \right)\). Tìm tọa độ của các điểm \({A_1},{A_2},{A_3}\).
Phương pháp:
Hình chiếu của một điểm lên mặt phẳng tọa độ sẽ giữ nguyên hai tọa độ tương ứng với mặt phẳng đó và tọa độ còn lại sẽ bằng 0.
Lời giải:
Gọi A1(x1; y1; z1), A2(x2; y2; z2) và A3(x3; y3; z3).
Với A(3; – 2; – 1), đặt xA = 3, yA = – 2, zA = – 1. Ta có:
+ x1 = xA = 3; y1 = yA = – 2; z1 = 0 (vì A1 nằm trên mặt phẳng (Oxy)).
Do đó A1(3; – 2; 0).
+ y2 = yA = – 2; z2 = zA = – 1; x2 = 0 (vì A2 nằm trên mặt phẳng (Oyz)).
Do đó A2(0; – 2; – 1).
+ x3 = xA = 3; z3 = zA = – 1; y3 = 0 (vì A3 nằm trên mặt phẳng (Ozx)).
Do đó A3(3; 0; – 1).
Bài 7 trang 73 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( { - 2;3;4} \right)\). Gọi \(H,K,P\) lần lượt là hình chiếu của điểm \(A\) trên các trục \(Ox,Oy,Oz\). Tìm tọa độ của các điểm \(H,K,P\).
Phương pháp:
Hình chiếu của một điểm lên mặt phẳng tọa độ sẽ giữ nguyên hai tọa độ tương ứng với mặt phẳng đó và tọa độ còn lại sẽ bằng 0.
Lời giải:
Gọi H(x1; y1; z1), K(x2; y2; z2) và P(x3; y3; z3).
Với A(– 2; 3; 4), đặt xA = – 2, yA = 3, zA = 4. Ta có:
+ x1 = xA = – 2; y1 = 0; z1 = 0 (vì H nằm trên trục Ox). Do đó H(– 2; 0; 0).
+ y2 = yA = 3; x2 = 0; z2 = 0 (vì K nằm trên trục Oy). Do đó K(0; 3; 0).
+ z3 = zA = 4; x3 = 0; y3 = 0 (vì P nằm trên trục Oz). Do đó P(0; 0; 4).
Bài 8 trang 73 SGK Toán 12 Tập 1 Cánh Diều
Trong không gian với hệ tọa độ \(Oxyz\), cho hình hộp có \(A\left( {4;6; - 5} \right),B\left( {5;7; - 4} \right)\);. Tìm tọa độ các đỉnh còn lại của hình hộp .
Phương pháp:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}\)).
Lời giải:
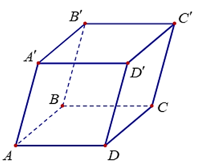

Suy ra C'(3; 1; 3).
Vậy D(4; 5; – 5), A'(2; 1; 2), B'(3; 2; 3), C'(3; 1; 3).
Bài 9 trang 73 SGK Toán 12 Tập 1 Cánh Diều
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.
Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ \(Oxyz\) (đơn vị độ dài trên mỗi trục là 1 m), các đỉnh của bốn chiếc cột lần lượt là các điểm \(M\left( {90;0;30} \right),N\left( {90;120;30} \right)\),\(P\left( {0;\;120;\;30} \right),Q\left( {0;\;0;\;30} \right)\) (Hình 34)
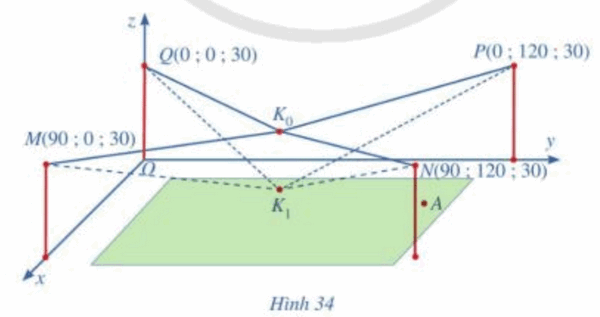
Giả sử \({K_0}\) là vị trí ban đầu của camera có cao độ bằng 25 và \({K_0}M = {K_0}N = {K_0}P = {K_0}Q\). Để theo dõi quả bóng đến vị trí \(A\), camera được hạ thấp theo phương thẳng đứng xuống điểm \({K_1}\) cao độ bằng 19. tìm các điểm \({K_0},{K_1}\) và vector \(\overrightarrow {{K_0}{K_1}} \)
Phương pháp:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}\)).
Lời giải:
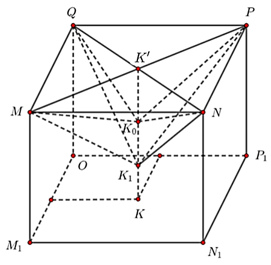
Gọi M1, N1, P1, K lần lượt là hình chiếu của M, N, P, K0 lên mặt phẳng (Oxy).
Ta thấy MNPQ.M1N1P1O là hình hộp chữ nhật.
Gọi K' là giao hai đường chéo MP và NQ. Khi đó K'Q = K'P = K'N = K'M.
Vì K0M = K0N = K0P = K0Q và camera được hạ thấp theo phương thẳng đứng từ điểm K0 xuống điểm K1 nên các điểm K', K0, K1, K thẳng hàng.
Khi đó, các điểm K', K0, K1, K có hoành độ và tung độ bằng nhau.
Theo bài ra, cao độ của K0 và K1 lần lượt là 25 và 19.
Giả sử K0(x; y; 25) và K1(x; y; 19).
Ta có MNPQ.M1N1P1O là hình hộp chữ nhật nên K'K = OQ, suy ra cao độ của K' bằng 30. Do đó, K' (x; y; 30).
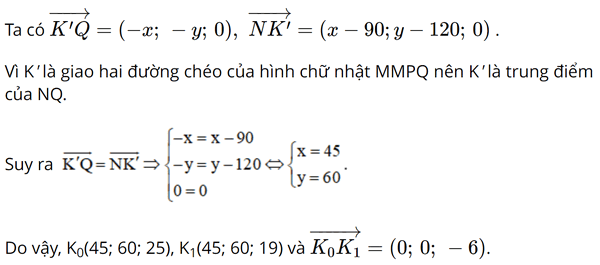
Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 3
- Bài 2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm
- Bài 1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
- CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO MẪU SỐ LIỆU GHÉP NHÓM
- Bài tập cuối chương 2
- Bài 3. Biểu thức toạ độ của các phép toán vectơ
- Bài 2. Toạ độ của vectơ
- Bài 1. Vectơ và các phép toán vectơ trong không gian
- CHƯƠNG II. TỌA ĐỘ VECTƠ TRONG KHÔNG GIAN
- Bài tập cuối chương 1
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
