Giải SGK Toán 12 tập 1 Kết nối tri thức trang 13, 14
Giải bài 1.1, 1.2, 1.3, 1.4, 1.5 trang 13, bài 1.6, 1.7, 1.8, 1.9 trang 14 SGK Toán 12 Kết nối tri thức tập 1. Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số N(t)= 25t+10 / t+5 ,t≥0, trong đó N(t) được tính bằng nghìn người.
Bài 1.1 trang 13 SGK Toán 12 Tập 1 Kết nối tri thức
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
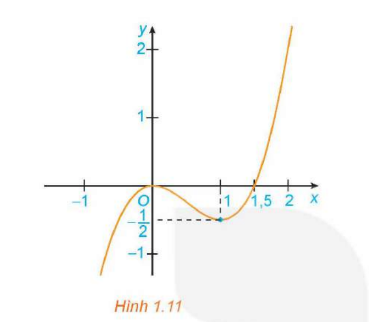
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
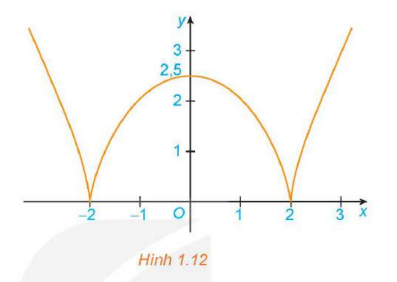
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) (H.1.12).
Phương pháp:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến của hàm số:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải:
a) Dựa vào đồ thị hàm số ta có:
Hàm số đồng biến trên các khoảng (−∞; 0) và (1; +∞).
Hàm số nghịch biến trên khoảng (0; 1).
b) Dựa vào đồ thị hàm số ta có:
Hàm số đồng biến trên các khoảng (−2; 0) và (2; +∞).
Hàm số nghịch biến trên các khoảng (−∞; −2) và (0; 2).
Bài 1.2 trang 13 SGK Toán 12 Tập 1 Kết nối tri thức
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Phương pháp:
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét sự đồng biến, nghịch biến của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) Tập xác định của hàm số là ℝ.
Có y' = x2 – 4x + 3.
Hàm số đồng biến khi y' > 0 ⇔">⇔ x2 – 4x + 3 > 0 ⇔x<1x>3">⇔ 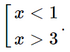
Hàm số nghịch biến khi y' < 0 ⇔ x2 – 4x + 3 < 0 ⇔ 1 < x < 3.
Do đó hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞); nghịch biến trên khoảng (1; 3).
b) Tập xác định của hàm số là ℝ.
Có y' = −3x2 + 4x – 5
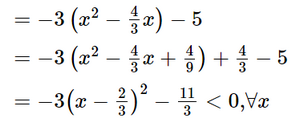
Do đó hàm số luôn nghịch biến.
Bài 1.3 trang 13 SGK Toán 12 Tập 1 Kết nối tri thức
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Phương pháp:
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét khoảng đồng biến của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) Tập xác định của hàm số là ℝ\{−2}.
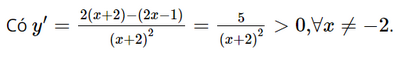
Lập bảng biến thiên của hàm số
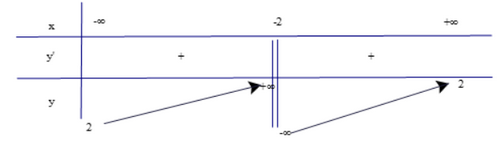
Dựa vào bảng biến thiên ta có:
Hàm số đồng biến trên cách khoảng (−∞; −2) và (−2; +∞).
b) Tập xác định của hàm số là ℝ\{3}.
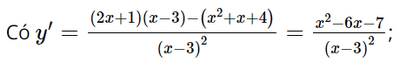
Có y' = 0 ⇔ x2 – 6x – 7 = 0 ⇔ x = −1 hoặc x = 7.
Lập bảng biến thiên của hàm số
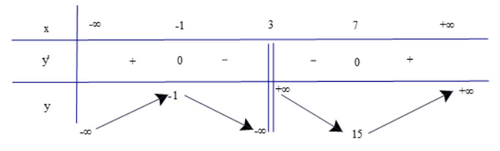
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng (−∞; −1) và (7; +∞).
Hàm số nghịch biến trên các khoảng (−1; 3) và (3; 7).
Bài 1.4 trang 13 SGK Toán 12 Tập 1 Kết nối tri thức
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Phương pháp:
Sử dụng kiến thức về các bước để xét tính đơn điệu để xét chiều biến thiên của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) Tập xác định của hàm số là D = [−2; 2].
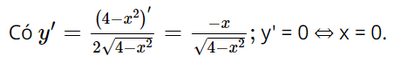
Lập bảng biến thiên của hàm số
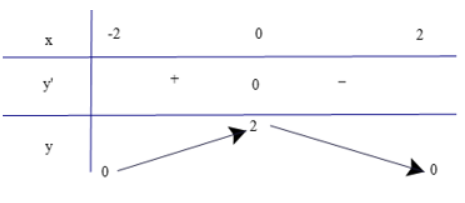
Dựa vào bảng biến thiên, ta có
Hàm số đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 2).
b) Tập xác định của hàm số là ℝ.
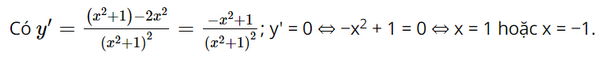
Lập bảng biến thiên của hàm số
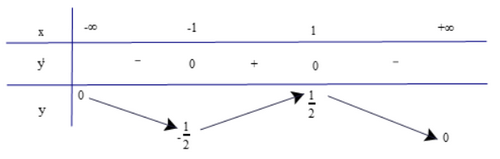
Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng (−1; 1).
Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).
Bài 1.5 trang 13 SGK Toán 12 Tập 1 Kết nối tri thức
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \(N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \ge 0\), trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Phương pháp:
Sử dụng kiến thức về định lí về tính đồng biến của hàm số để chứng minh: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K. Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
Lời giải:
a) Số dân vào năm 2000 (t = 0) của thị trấn đó là: 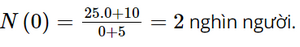
Sau 15 năm kể từ năm 2000 số dân của thị trấn đó là: 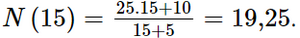
Vậy số dân của thị trấn đó vào năm 2015 là 19250 người.
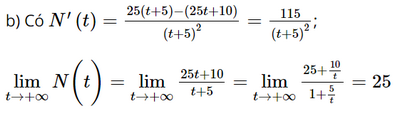
Vì N'(t) > 0, ∀t do đó hàm số N(t) là hàm đồng biến hơn nữa
Bài 1.6 trang 14 SGK Toán 12 Tập 1 Kết nối tri thức
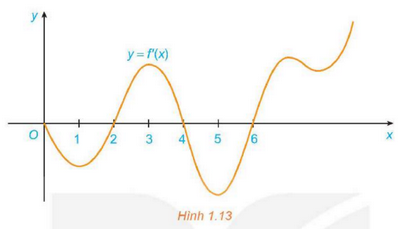
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Phương pháp:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để giải: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
Lời giải:
Dựa vào đồ thị của hàm y = f'(x), ta có bảng biến thiên của hàm số y = f(x) như sau
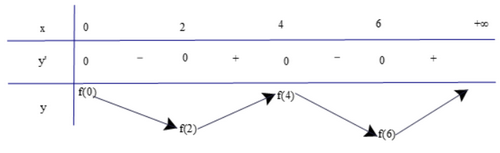
a) Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng (2; 4) và (6; +∞).
b) Dựa vào bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại x = 2 và x = 6.
Hàm số đạt cực đại tại x = 4.
Bài 1.7 trang 14 SGK Toán 12 Tập 1 Kết nối tri thức
Tìm cực trị của các hàm số sau:
a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);\(y = {x^4} - 4{x^2} + 2\)
b) 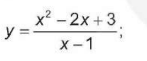
c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);
d) \(y = \sqrt {4x - 2{x^2}} \).
Phương pháp:
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải:
a) Tập xác định của hàm số là ℝ.
Có y' = 6x2 – 18x + 12; y' = 0 ⇔ x = 1 hoặc x = 2.
Lập bảng biến thiên của hàm số
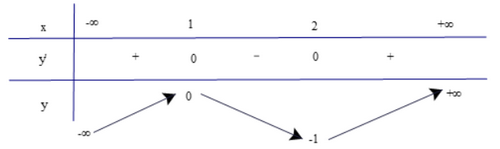
Dựa vào bảng biến thiên, ta có
Hàm số đạt cực đại tại x = 1 và yCĐ = 0.
Hàm số đạt cực tiểu tại x = 2 và yCT = −1.
b) Tập xác định của hàm số là ℝ.
Có y' = 4x3 – 8x; y' = 0 ⇔ x = 0 hoặc x=−2">
Lập bảng biến thiên của hàm số
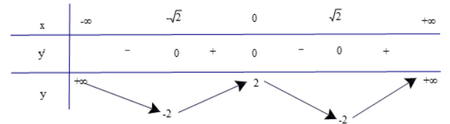
Dựa vào bảng biến thiên, ta có:
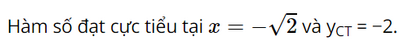
Hàm số đạt cực đại tại x = 0 và yCĐ = 2.
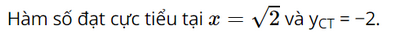
c) Tập xác định của hàm số là ℝ\{1}.
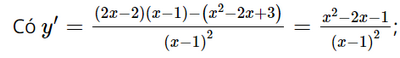
Có y' = 0 ⇔ x2 – 2x – 1 = 0 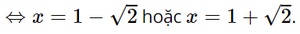
Lập bảng biến thiên của hàm số
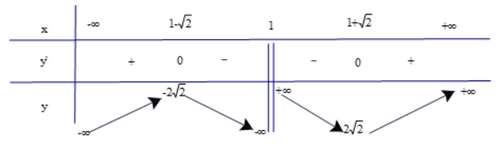
Dựa vào bảng biến thiên, ta có:
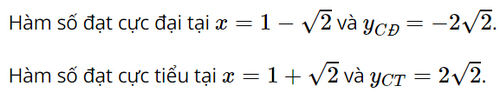
d) Tập xác định của hàm số là D = [0; 2].
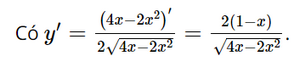
Có y' = 0 ⇔ x = 1.
Lập bảng biến thiên của hàm số
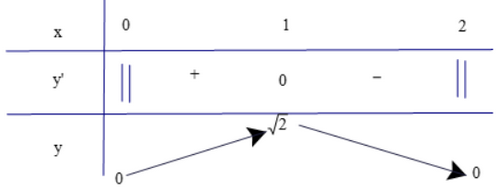
Dựa vào bảng biến thiên ta có:
Hàm số đạt cực đại tại x = 1 và 
Hàm số không có cực tiểu.
Bài 1.8 trang 14 SGK Toán 12 Tập 1 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \left| x \right|\).
a) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) và \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Từ đó suy ra hàm số không có đạo hàm tại \(x = 0\).
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại \(x = 0\). (Xem Hình 1.4)
Phương pháp:
Sử dụng kiến thức về cực trị hàm số để tìm cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\). Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải:
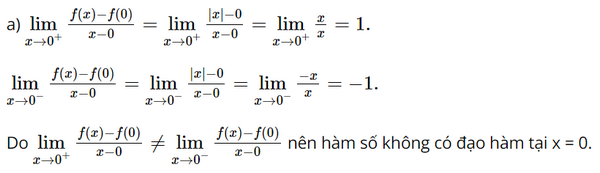
b) Theo định nghĩa, hàm số f(x) đạt cực tiểu tại x = x0 nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x ∈ (x0 – h; x0 + h) và x ≠ x0 .
Ở đây, x0 = 0. Ta sẽ chứng minh rằng tồn tại số h > 0 sao cho f(x) > f(0) với mọi x ∈ (– h; h).
Với mọi x ∈ (– h; h), ta có |x| < h.
Mà |x| > 0, với mọi x ≠ 0. Do đó f(x) = |x| > 0 = f(0), với mọi x ∈ (– h; h) và x ≠ 0.
Vậy ta chứng minh được rằng với mọi x ∈ (– h; h) và x ≠ x0, f(x) > f(0). Điều này chứng tỏ rằng hàm số có cực tiểu tại x = 0.
Bài 1.9 trang 14 SGK Toán 12 Tập 1 Kết nối tri thức
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\;000}}{{1 + 5{e^{ - t}}}},t \ge 0,\) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Phương pháp:
Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải:
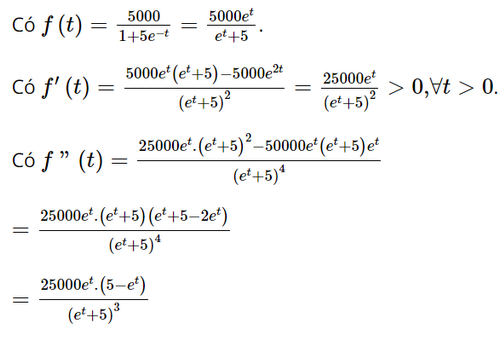
Có f"(t) = 0 ⇔ 5 – et = 0 ⇔ t = ln5.
Ta có bảng biến thiên
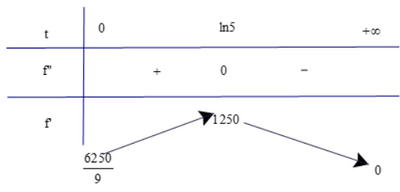
Dựa vào bảng biến thiên ta có sau ln5 năm thì tốc độ bán hàng là lớn nhất.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Chương 4: Nguyên hàm và tích phân
- Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra
- Bài tập cuối chương 3
- Bài 10: Phương sai và độ lệch chuẩn
- Bài 9: Khoảng biến thiên và khoảng tứ phân vị
- Chương 3: Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm
- Bài tập cuối chương 2
- Bài 8: Biểu thức toạ độ của các phép toán vectơ
- Bài 7: Hệ trục toạ độ trong không gian
- Bài 6: Vectơ trong không gian
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
