Giải SGK Toán 12 tập 1 Kết nối tri thức trang 72
Giải bài 2.20, 2.21, 2.22, 2.23, 2.24 trang 72 SGK Toán 12 Kết nối tri thức tập 1. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
Bài 2.20 trang 72 SGK Toán 12 Tập 1 Kết nối tri thức
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {3;1;2} \right)\), \(\overrightarrow b = \left( { - 3;0;4} \right)\) và \(\overrightarrow c = \left( {6; - 1;0} \right)\)
a) Tìm tọa độ của các vectơ \(\overrightarrow a + \overrightarrow b + \overrightarrow c \) và \(2\overrightarrow a - 3\overrightarrow b - 5\overrightarrow c \).
b) Tính các tích vô hướng \(\overrightarrow a .\left( { - \overrightarrow b } \right)\) và \(\left( {2\overrightarrow a } \right).\overrightarrow c \).
Phương pháp:
Sử dụng kiến thức hệ về biểu thức tọa độ của phép cộng hai vectơ, phép nhân một số với một vectơ, tích vô hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\). Ta có:
+ \(\overrightarrow a + \overrightarrow b = \left( {x + x';y + y';z + z'} \right)\)
+ \(\overrightarrow a - \overrightarrow b = \left( {x - x';y - y';z - z'} \right)\)
+ \(k\overrightarrow a = \left( {kx;ky;kz} \right)\) với k là một số thực.
+ \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\).
Lời giải:
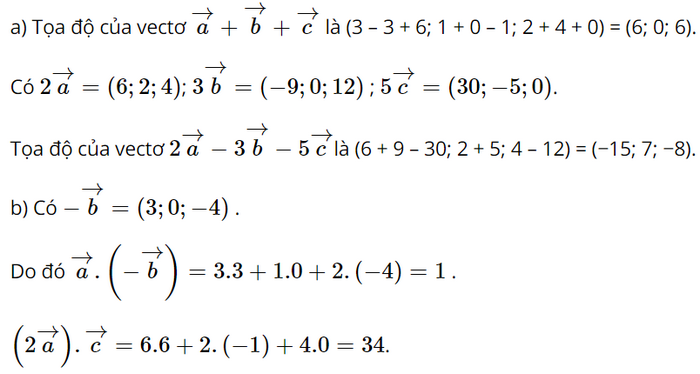
Bài 2.21 trang 72 SGK Toán 12 Tập 1 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm \(M\left( { - 4;3;3} \right),N\left( {4; - 4;2} \right)\) và \(P\left( {3;6; - 1} \right)\).
a) Tìm tọa độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \), từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
b) Tìm tọa độ của vectơ \(\overrightarrow {NM} + \overrightarrow {NP} \), từ đó suy ra tọa độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
c) Tính chu vi của hình bình hành MNPQ.
a) Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).
+ Sử dụng kiến thức về hai vectơ không cùng phương để chứng minh ba điểm không thẳng hàng: Nếu hai vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) không cùng phương thì ba điểm M, N, P không thẳng hàng.
b) Sử dụng quy tắc hình bình hành để tìm tọa độ điểm Q: Để tứ giác MNPQ là hình bình hành thì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow {NQ} \)
Sử dụng kiến thức hệ về biểu thức tọa độ của phép cộng hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) thì \(\overrightarrow a + \overrightarrow b = \left( {x + x';y + y';z + z'} \right)\)
c) Sử dụng kiến về chu vi hình bình hành để tính: Chu vi hình bình hành MNPQ là: \(C = 2\left( {MN + NP} \right)\).
Lời giải:
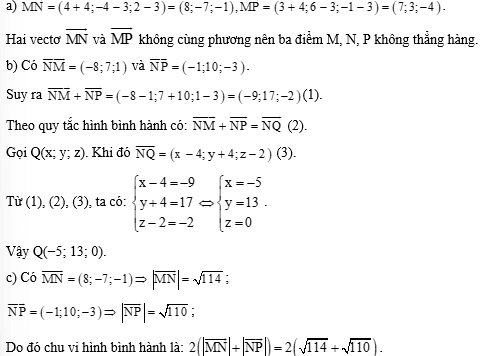
Bài 2.22 trang 72 SGK Toán 12 Tập 1 Kết nối tri thức
Trong không gian Oxyz, cho tam giác ABC có \(A\left( {1;0;1} \right),B\left( {0; - 3;1} \right)\) và \(C\left( {4; - 1;4} \right)\).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Chứng minh rằng \(\widehat {BAC} = {90^0}\).
c) Tính \(\widehat {ABC}\).
Phương pháp:
a) Sử dụng kiến thức về công thức tọa độ trọng tâm của tam giác để tính: Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) và \(C\left( {{x_C};{y_C};{z_C}} \right)\) thì tọa độ trọng tâm của tam giác ABC là: \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\).
b) Sử dụng kiến thức về nhận xét biểu thức tọa độ tích vô hướng trong không gian để chứng minh: Trong không gian Oxyz, cho \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) là hai vectơ khác \(\overrightarrow 0 \). Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc với nhau nếu và chỉ nếu \(xx' + yy' + zz' = 0\)
c) Sử dụng kiến thức về độ dài đoạn thẳng trong không gian để tính: Nếu \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải:

Bài 2.23 trang 72 SGK Toán 12 Tập 1 Kết nối tri thức
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
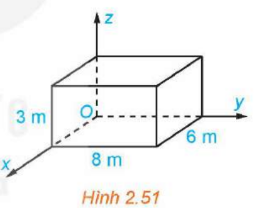
Phương pháp:
Sử dụng kiến thức về tọa độ trung điểm của đoạn thẳng để tính: Trong không gian Oxyz, cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\). Khi đó, tọa độ trung điểm của đoạn thẳng AB là: \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\).
Lời giải:
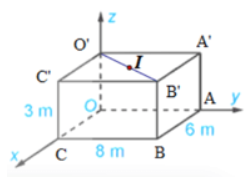
Giả sử căn phòng hình hộp chữ nhật được mô phỏng như hình vẽ.
Khi đó ta có B' (6; 8; 3) và O'(0; 0; 3).
Gọi I là điểm chính giữa trần nhà của phòng học.
Vì O'A'B'C' là hình chữ nhật nên I là trung điểm của O'B'.
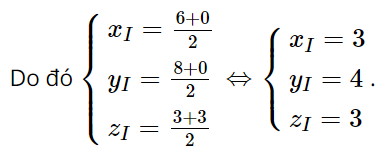
Vậy tọa độ điểm treo đèn là (3; 4; 3).
Bài 2.24 trang 72 SGK Toán 12 Tập 1 Kết nối tri thức
Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời (H.2.52). Đơn vị đo trong không gian Oxyz lấy theo kilômét. Một chiếc ra đa đặt tại giàn khoan có phạm vi theo dõi là 30km. Hỏi ra đa có thể phát hiện được một chiếc tàu thám hiểm có tọa độ là (25; 15; -10) đối với hệ tọa độ nói trên hay không? Hãy giải thích vì sao.

Phương pháp:
Sử dụng kiến thức về độ dài đoạn thẳng trong không gian để tính: Nếu \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \)
Lời giải:
Để xác định xem ra đa có thể phát hiện được tàu thám hiểm hay không, ta cần xác định khoảng cách giữa ra đa và tàu thám hiểm.
Theo đề ta có tọa độ của ra đa là (0; 0; 0), tọa độ của tàu thám hiểm là (25; 15; −10).
Khi đó khoảng cách giữa ra đa và tàu thám hiểm là:
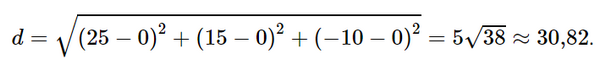
Vì phạm vi theo dõi của ra đa là 30 km mà khoảng khoảng cách giữa ra đa và tàu thám hiểm là 30,82 km nên ra đa không phát hiện được tàu thám hiểm.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Chương 4: Nguyên hàm và tích phân
- Khảo sát và vẽ đồ thị hàm số với phần mềm GeoGebra
- Bài tập cuối chương 3
- Bài 10: Phương sai và độ lệch chuẩn
- Bài 9: Khoảng biến thiên và khoảng tứ phân vị
- Chương 3: Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm
- Bài tập cuối chương 2
- Bài 8: Biểu thức toạ độ của các phép toán vectơ
- Bài 7: Hệ trục toạ độ trong không gian
- Bài 6: Vectơ trong không gian
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
