Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 trang 123, 124, 125, 126 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo

Bài 1 trang 123 SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Gieo một con xúc xắc 4 mặt 24 lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Gieo được đỉnh ghi số 2.

b) Gieo được đỉnh ghi số lẻ.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số lần gieo được đỉnh ghi số 2 là: 6;

Tổng số lần gieo là : 24.

Vậy xác suất thực nghiệm của sự kiện “Gieo được đỉnh ghi số 2” là: 6/24 = 0,25

b) Các số lẻ xuất hiện trong các lần gieo là 1 và 3.

Số lần gieo được đỉnh ghi số 1 là: 5;

Số lần gieo được đỉnh ghi số 3 là: 6.

Số lần gieo được đỉnh ghi số lẻ (tức là số lần gieo ghi đỉnh số 1 hoặc số 3) là: 5+ 6 = 11.

Tổng số lần gieo là: 24.

Vậy xác suất thực nghiệm của sự kiện “Gieo được đỉnh ghi số lẻ” là: 11/24

Bài 2 trang 123- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

 Bình ghi lại số bạn đi học muộn của lớp trong 20 ngày liên tiếp. Kết quả cho ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:

a) Một ngày có đúng 3 bạn đi học muộn.

b) Một ngày không có bạn nào đi học muộn.

c) Một ngày có bạn đi học muộn.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số ngày có đúng 3 bạn đi học muộn trong 20 ngày là: 1.

Vậy xác suất thực nghiệm của sự kiện “Một ngày có đúng 3 bạn đi học muộn” là: 1/20 = 0,05

b) Số ngày không có bạn nào đi học muộn trong 20 ngày là: 10.

Vậy xác suất thực nghiệm của sự kiện “Một ngày không có bạn nào đi học muộn” là: 10/20 = 0,5

c) Số ngày có bạn đi học muộn (nghĩa là có thể có 1 bạn đi học muộn hoặc 2 bạn đi học muộn hoặc 3 bạn đi học muộn) trong 20 ngày là: 10.

Vậy xác suất thực nghiệm của sự kiện “Một ngày có bạn đi học muộn” là: 10/20 = 0,5

Bài 3 trang 123- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Trong hộp có 4 thẻ được đánh số 1, 2, 3, 4. Thảo nhắm mắt lấy ra 1 thẻ từ hộp, ghi số rồi trả lại hộp. Lặp lại hoạt động trên 20 lần, Thảo được bảng kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Thảo lấy được thẻ ghi số chẵn.

b) Thảo lấy được thẻ ghi số nguyên tố.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Các thẻ số chẵn trong bảng trên là: thẻ ghi số 2 và số 4.

Số lần Thảo lấy được thẻ ghi số 2 là: 5.

Số lần Thảo lấy được thẻ ghi số 4 là: 5.

Số lần Thảo lấy được thẻ ghi số chẵn (thẻ ghi số 2 hoặc số 4) trong 20 lần là: 5 + 5 = 10

Vậy xác suất thực nghiệm của sự kiện “Thảo lấy được thẻ ghi số chẵn” là: 10/20 = 0,5

b) Các thẻ số nguyên tố trong bảng trên là: thẻ ghi số 2 và số 3.

Số lần Thảo lấy được thẻ ghi số 2 là 5.

Số lần Thảo lấy được thẻ ghi số 3 là 5.

Số lần Thảo lấy được thẻ ghi số nguyên tố (thẻ ghi số 2 hoặc số 3) trong 20 lần là: 5 + 5 = 10.

Vậy xác suất thực nghiệm của sự kiện “Thảo lấy được thẻ ghi số nguyên tố” là: 10/20 = 0,5

Bài 4 trang 124- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

 Một xạ thủ bắn 20 mũi tên vào một tấm bia. Điểm số của các lần bắn cho ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện sau trong mỗi lần bắn:

a) Xạ thủ bắn được 10 điểm.

b) Xạ thủ bắn được ít nhất 8 điểm.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số lần xạ thủ bắn được 10 điểm trong 20 lần bắn là: 5

Vậy xác suất thực nghiệm của sự kiện “Xạ thủ bắn được 10 điểm” là: 5/20 = 0,25

b) Số lần xạ thủ bắn được ít nhất 8 điểm là số lần xạ thủ bắn được là 8 điểm hoặc hơn 8 điểm.

Do đó số lần xạ thủ bắn được ít nhất 8 điểm bằng tổng số lần bắn được 8 điểm, 9 điểm và 10 điểm.

Số lần xạ thụ bắn xạ thủ bắn được 8 điểm là: 5.

Số lần xạ thụ bắn xạ thủ bắn được 9 điểm là: 6.

Số lần xạ thụ bắn xạ thủ bắn được 10 điểm là: 5.

Số lần xạ thủ bắn được ít nhất 8 điểm trong 20 lần bắn là: 5 + 6 + 5 = 16

Vậy xác suất thực nghiệm của sự kiện “Xạ thủ bắn được ít nhất 8 điểm” là: 16/20 = 0,8

Bài 5 trang 124- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Tung hai đồng xu cân đối 100 lần ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Có một đồng xu sấp, một đồng xu ngửa.

b) Hai đồng xu đều sấp.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số lần tung được một đồng xu sấp, một đồng xu ngửa trong 100 lần tung là: 48.

Vậy xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là: 48/100 = 0.48

b) Số lần tung được hai đồng xu sấp trong 100 lần tung là: 20.

Vậy xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là: 20/100 = 0,2

Bài 6 trang 124 -SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Khảo sát năng suất lúa (tạ/ha) của 25 thửa ruộng được lựa chọn ngẫu nhiên người ta thu được bảng kết quả sau:

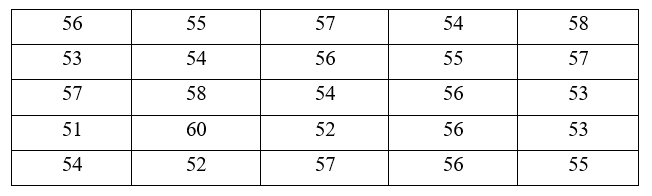
Hãy tính xác suất thực nghiệm của sự kiện:

a) Thửa ruộng được chọn có năng suất 55 tạ/ha.

b) Thửa ruộng được chọn có năng suất không quá 55 tạ/ha.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số thửa ruộng đạt 55 tạ/ha trong 25 thửa ruộng được chọn là: 3.

Vậy xác suất thực nghiệm của sự kiện “Thửa ruộng được chọn có năng suất 55 tạ/ha” là: 3/25 = 0,12

b) Các thửa ruộng đạt không quá 55 tạ/ha là các thửa ruộng có năng suất 55 tạ/ha hoặc nhỏ hơn 55 tạ/ha.

Do đó số thửa ruộng đạt không quá 55 tạ/ha bằng tổng các thửa ruộng có năng suất đạt 51 tạ/ha, 52 tạ/ha, 53 tạ/ha, 54 tạ/ha và 55 tạ/ha.

Số thửa ruộng đạt 51 tạ/ha là 1.

Số thửa ruộng đạt 52 tạ/ha là 2.

Số thửa ruộng đạt 53 tạ/ha là 3.

Số thửa ruộng đạt 54 tạ/ha là 4.

Số thửa ruộng đạt 55 tạ/ha là 3.

Do đó số thửa ruộng đạt không quá 55 tạ/ha trong 25 thửa ruộng được chọn là: 1+ 2 + 3 + 4 + 3 = 13.

Vậy xác suất thực nghiệm của sự kiện “Thửa ruộng được chọn có năng suất không quá 55 tạ/ha” là: 13/25 = 0,52

Bài 7 trang 125 -SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Số xe máy một cửa hàng bán được trong 30 ngày của tháng 4 được cho ở bảng sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Cửa hàng bán được 7 xe máy một ngày.

b) Cửa hàng bán được trên 5 xe máy một ngày.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số ngày cửa hàng bán được 7 xe máy trong 30 ngày là 6.

Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được 7 xe máy một ngày” là: 6/30 = 0,2

b) Số ngày cửa hàng bán được trên 5 xe máy bằng tổng số các ngày cửa hàng bán được 6 xe máy, 7 xe máy, 8 xe máy, 9 xe máy và 12 xe máy.

Số ngày cửa hàng bán được 6 xe máy là: 2.

Số ngày cửa hàng bán được 7 xe máy là: 6.

Số ngày cửa hàng bán được 8 xe máy là: 3.

Số ngày cửa hàng bán được 9 xe máy là: 3.

Số ngày cửa hàng bán được 12 xe máy là: 1

Số ngày cửa hàng bán được trên 5 xe máy trong 30 ngày là:

2 + 6 + 3 + 3 + 1 = 15.

Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được trên 5 xe máy một ngày” là: 15/30 = 0,5

Bài 8 trang 125 -SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Các bạn học sinh lớp 6B chơi trò gieo đồng xu như sau: Mỗi bạn sẽ gieo đồng xu của mình cho tới khi nào xuất hiện mặt sấp thì dừng lại. Sau đó mỗi bạn sẽ ghi lại số lần gieo mình đã thực hiện. Kết quả của cả lớp được tổng hợp lại trong bảng sau:

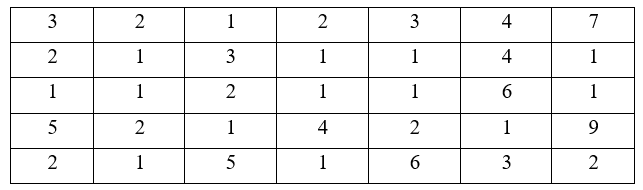
Hãy tính xác suất thực nghiệm của sự kiện:

a) Một bạn chỉ cần gieo một lần đã được mặt sấp.

b) Một bạn phải gieo ít nhất 3 lần mới được mặt sấp

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

Tổng số học sinh cả lớp là: 35.

a) Số bạn chỉ cần gieo một lần đã được mặt sấp là: 14.

Vậy xác suất thực nghiệm của sự kiện “Một bạn chỉ cần gieo một lần đã được mặt sấp” là: 14/35 = 0,4

b) Số bạn phải gieo ít nhất 3 lần mới được mặt sấp là: 13.

Vậy xác suất thực nghiệm của sự kiện “Một bạn phải gieo ít nhất 3 lần mới được mặt sấp” là: 13/35

Bài 9 trang 125 -SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Tỉ số 20 trận thi đấu gần đây nhất giữa hai đội bóng A và B được cho ở bảng sau:

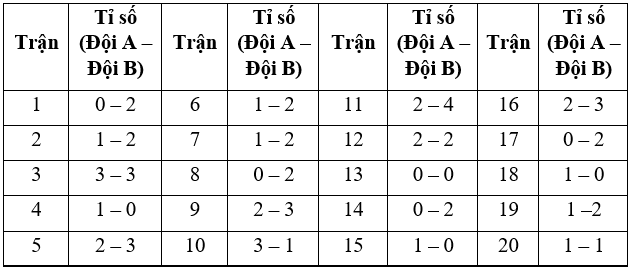
Hãy tính xác suất thực nghiệm của sự kiện sau trong mỗi trận đấu:

a) Đội A thắng đội B.

b) Hai đội hoà nhau.

c) Đội B ghi được hơn 1 bàn thắng.

d) Tổng số bàn thắng hai đội ghi được lớn hơn 2.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số trận mà đội A thắng đội B trong 20 trận gần đây là: 4 (là trận 4, trận 10, trận 15 và trận 18).

Vậy xác suất thực nghiệm của sự kiện “Đội A thắng đội B” là: 4/20 = 0,2

b) Số trận mà hai đội hoà nhau trong 20 trận gần đây là: 4 (là trận 3, trận 12, trận 13 và trận 20).

Vậy xác suất thực nghiệm của sự kiện “Hai đội hoà nhau” là: 4/20 = 0,2

c) Số trận mà đội B ghi được hơn 1 bàn thắng trong 20 trận gần đây là: 14 (Trừ các trận 4, trận 10, trận 13, trận 15, trận 18 và trận 20).

Vậy xác suất thực nghiệm của sự kiện “Đội B ghi được hơn 1 bàn thắng” là: 14/20 = 0,7

d) Số trận mà hai đội ghi được số bàn thắng lớn hơn 2 trong 20 trận gần đây là: 11 (là trận 2, trận 3, trận 5, trận 6, trận 7, trận 9, trận 10, trận 11, trận 12, trận 16 và trận 19).

Vậy xác suất thực nghiệm của sự kiện “Tổng số bàn thắng hai đội ghi được lớn hơn 2” là: 11/20 = 0,55

Bài 10 trang 126 -SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Thái thực hiện một điều tra về mối liên quan giữa thuốc lá và bệnh đường hô hấp. Em đã hỏi ngẫu nhiên 20 nam giới ở độ tuổi từ 40 đến 50 và được bảng kết quả như sau:

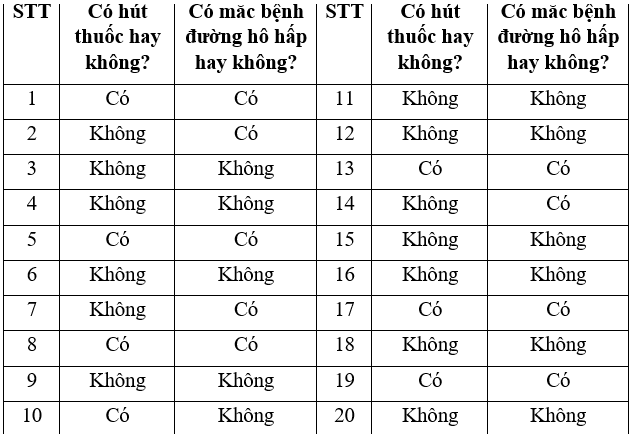
Hãy tính xác suất thực nghiệm của sự kiện:

a) Người được hỏi có hút thuốc.

b) Người được hỏi không mắc bệnh đường hô hấp.

c) Người được hỏi có hút thuốc và bị mắc bệnh đường hô hấp.

d) Người được hỏi không hút thuốc và không mắc bệnh đường hô hấp.

Phương pháp:

Xác suất thực nghiệm của sự kiện A là: n(A) : n

Với n(A) là số lần sự kiện A xảy ra, n là tổng số lần thực hiện hoạt động.

Trả lời:

a) Số người có hút thuốc trong số 20 người được hỏi là: 7.

Vậy xác suất thực nghiệm của sự kiện “Người được hỏi có hút thuốc” là: 7/20 = 0,35

b) Số người không mắc bệnh đường hô hấp trong số 20 người được hỏi là: 11.

Vậy xác suất thực nghiệm của sự kiện “Người được hỏi không mắc bệnh đường hô hấp” là: 11/20 = 0,55

c) Số người có hút thuốc và bị mắc bệnh đường hô hấp trong số 20 người được hỏi là: 6.

Vậy xác suất thực nghiệm của sự kiện “Người được hỏi có hút thuốc và bị mắc bệnh đường hô hấp” là: 6/20 = 0,3

d) Số người không hút thuốc và không mắc bệnh đường hô hấp trong số 20 người được hỏi là: 3.

Vậy xác suất thực nghiệm của sự kiện “Người được hỏi không hút thuốc và không mắc bệnh đường hô hấp” là: 3/20 = 0,15

Sachbaitap.com