Bài 32, 33, 34, 35, 36, 37 trang 19, 20 SGK Toán 9 tập 1 - Luyện tập

Bài 32 trang 19 SGK Toán lớp 9 tập 1

Câu hỏi:

Tính:

a) \( \sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}\)

b) \( \sqrt{1,44.1,21-1,44.0,4}\)

c) \( \sqrt{\dfrac{165^{2}-124^{2}}{164}}\)

d) \( \sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}\)

Lời giải: 

a) 

Ta có:

\(\sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}=\sqrt{\dfrac{1.16+9}{16}.\dfrac{5.9+4}{9}.\dfrac{1}{100}}\)

\(=\sqrt{\dfrac{16+9}{16}.\dfrac{45+4}{9}.\dfrac{1}{100}}\)

\(=\sqrt{\dfrac{25}{16}.\dfrac{49}{9}.\dfrac{1}{100}}\)

\(=\sqrt{\dfrac{25}{16}}.\sqrt{\dfrac{49}{9}}.\sqrt{\dfrac{1}{100}}\)

\(=\dfrac{\sqrt{25}}{\sqrt{16}}.\dfrac{\sqrt{49}}{\sqrt{9}}.\dfrac{\sqrt{1}}{\sqrt{100}}\)

\(=\dfrac{\sqrt{5^2}}{\sqrt{4^2}}.\dfrac{\sqrt{7^2}}{\sqrt{3^2}}.\dfrac{1}{\sqrt{10^2}}\)

\(=\dfrac{5}{4}.\dfrac{7}{3}.\dfrac{1}{10}=\dfrac{5.7.1}{4.3.10}=\dfrac{35}{120}=\dfrac{7}{24}.\)

b) 

Ta có: 

\(\sqrt{1,44.1,21-1,44.0,4} \)\(= \sqrt{1,44(1,21-0,4)}\)

\(=\sqrt{1,44.0,81}\)

\(=\sqrt{1,44}.\sqrt{0,81}\)

\(=\sqrt{1,2^2}.\sqrt{0,9^2}\)

\(=1,2.0,9=1,08\).

c) 

Ta có: 

\(\sqrt{\dfrac{165^{2}-124^{2}}{164}}\)\(=\sqrt{\dfrac{(165-124)(165+124)}{164}}\)

\(=\sqrt{\dfrac{41.289}{41.4}}\) \(=\sqrt{\dfrac{289}{4}}\)

\(=\dfrac{\sqrt{289}}{\sqrt{4}}\) \(=\dfrac{\sqrt{17^2}}{\sqrt{2^2}}\) \(=\dfrac{17}{2}\).

d) 

Ta có:

\(\sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}\) \(=\sqrt{\dfrac{(149-76)(149+76)}{(457-384)(457+384)}}\)

\(=\sqrt{\dfrac{73.225}{73.841}}\) \(=\sqrt{\dfrac{225}{841}}\)

\(=\sqrt {\dfrac{15^2}{29^2}} = \sqrt {{{\left( {\dfrac{{15}}{{29}}} \right)}^2}}=\dfrac{15}{29}\).

Bài 33 trang 19 SGK Toán lớp 9 tập 1

Câu hỏi:

Giải phương trình

a) \(\sqrt 2 .x - \sqrt {50}  = 0\)

b) \(\sqrt 3 .x + \sqrt 3  = \sqrt {12}  + \sqrt {27}\)

c) \(\sqrt 3 .{x^2} - \sqrt {12}  = 0\)

d) \(\dfrac{x^2}{\sqrt 5 } - \sqrt {20}  = 0\)

Phương pháp: 

Sử dụng các công thức 

+ \(\sqrt {AB}  = \sqrt A .\sqrt B \,\left( {A;B \ge 0} \right)\)

+ \(\dfrac{\sqrt A}{\sqrt B}=\sqrt{\dfrac{A}{B}}\) (với \( A\ge 0;B>0\))

+ \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}
A\,\,\,\,\,{\rm{khi}}\,\,A \ge 0\\
- A\,\,{\rm{khi}}\,\,A < 0
\end{array} \right.\)

Lời giải: 

a) 

\(\sqrt{2}.x - \sqrt{50} = 0\)

\(\Leftrightarrow \sqrt{2}x=\sqrt{50}\)

\(\Leftrightarrow x=\dfrac{\sqrt{50}}{\sqrt{2}}\)

\(\Leftrightarrow x =\sqrt{\dfrac{50}{2}}\)

\(\Leftrightarrow x= \sqrt{25}\)

\(\Leftrightarrow x= \sqrt{5^2}\)

\(\Leftrightarrow x=5\).

Vậy \(x=5\).

b) 

 \(\sqrt{3}.x + \sqrt{3} = \sqrt{12} + \sqrt{27}\)

\( \Leftrightarrow \sqrt{3}.x = \sqrt{12} + \sqrt{27} - \sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=\sqrt{4.3}+\sqrt{9.3}- \sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=\sqrt{4}. \sqrt{3}+\sqrt{9}. \sqrt{3}- \sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=\sqrt{2^2}. \sqrt{3}+\sqrt{3^2}. \sqrt{3}- \sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=2 \sqrt{3}+3\sqrt{3}- \sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=(2+3-1).\sqrt{3}\)

\(\Leftrightarrow \sqrt{3}.x=4\sqrt{3}\)

\(\Leftrightarrow x=4\).

Vậy \(x=4\).

c) 

\(\sqrt{3}x^2-\sqrt{12}=0\)

 \(\Leftrightarrow \sqrt{3}x^2=\sqrt{12}\)

\(\Leftrightarrow \sqrt{3}x^2=\sqrt{4.3}\)

\(\Leftrightarrow \sqrt{3}x^2=\sqrt{4}.\sqrt 3\)

\(\Leftrightarrow x^2=\sqrt{4}\)

\(\Leftrightarrow x^2=\sqrt{2^2}\)

\(\Leftrightarrow x^2=2\)

\(\Leftrightarrow \sqrt{x^2}=\sqrt{2}\)

\(\Leftrightarrow |x|= \sqrt 2\)

\(\Leftrightarrow x= \pm \sqrt 2\).

Vậy \(x= \pm\sqrt 2\).

d) 

 \(\dfrac{x^{2}}{\sqrt{5}}- \sqrt{20} = 0\)

\(\Leftrightarrow \dfrac{x^2}{\sqrt{5}}=\sqrt{20}\)

\(\Leftrightarrow x^2=\sqrt{20}.\sqrt{5}\)

\(\Leftrightarrow x^2=\sqrt{20.5}\)

\(\Leftrightarrow x^2=\sqrt{100}\)

\(\Leftrightarrow x^2=\sqrt{10^2}\)

\(\Leftrightarrow x^2=10\)

\(\Leftrightarrow \sqrt{x^2}=\sqrt {10}\)

\(\Leftrightarrow |x|=\sqrt{10}\)

\(\Leftrightarrow x=\pm \sqrt{10}\).

Vậy \(x= \pm \sqrt{10}\).

Bài 34 trang 19 SGK Toán lớp 9 tập 1

Câu hỏi:

Rút gọn các biểu thức sau:

a) \( ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}\) với \(a < 0,\ b ≠ 0\)

b) \( \sqrt{\dfrac{27(a - 3)^{2}}{48}}\) với \(a > 3\)

c) \( \sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}\) với \(a ≥ -1,5\) và \(b < 0.\)

d) \((a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}\) với \(a < b < 0\)

Phương pháp: 

Sử dụng các công thức:

+ \(\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt a}{\sqrt b}\) với \(a \ge 0; b>0\)

+ \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}
A\,\,\,\,\,{\rm{khi}}\,\,A \ge 0\\
- A\,\,{\rm{khi}}\,\,A < 0
\end{array} \right.\) 

Lời giải:  

a) 

Ta có:

\(ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}\) \(=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{b^4}}\)

\(=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{(b^2)^2}}\) \(=ab^2.\dfrac{\sqrt{3}}{|a|.|b^2|}\)

 \(=ab^2.\dfrac{\sqrt{3}}{-ab^2}=-\sqrt{3}\).

(Vì \(a < 0 \) nên \(|a|=-a\) và \(b \ne 0\) nên \(b^2 >0 \Rightarrow |b^2|=b^2) \).

b) 

Ta có:

\(\sqrt{\dfrac{27(a - 3)^{2}}{48}}=\sqrt{\dfrac{27}{48}.(a-3)^2}\) \(=\sqrt{\dfrac{27}{48}}.\sqrt{(a-3)^2}\)

\(=\sqrt{\dfrac{9.3}{16.3}}.\sqrt{(a-3)^2}\) \(=\sqrt{\dfrac{9}{16}}.\sqrt{(a-3)^2}\)

\(=\sqrt{\dfrac{3^2}{4^2}}.\sqrt{(a-3)^2}\) \(=\dfrac{\sqrt {3^2}}{\sqrt {4^2}}.\sqrt{(a-3)^2}\)

\(=\dfrac{3}{4}|a-3|=\dfrac{3}{4}(a-3)\).

( Vì \(a > 3\) nên \(a-3>0 \Rightarrow |a-3|=a-3) \)

c) 

Ta có:

\(\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=\sqrt{\dfrac{3^2+2.3.2a+2^2.a^2}{b^2}}\)

\(=\sqrt{\dfrac{3^2+2.3.2a+(2a)^2}{b^2}}=\sqrt{\dfrac{(3+2a)^2}{b^2}}\)

\(=\dfrac{\sqrt{(3+2a)^2}}{\sqrt{b^2}}=\dfrac{|3+2a|}{|b|}\)

Vì \(a \geq -1,5 \Rightarrow a+1,5>0\)

                      \(\Leftrightarrow 2(a+1,5)>0\) 

                      \( \Leftrightarrow  2a+3>0\)

                      \( \Leftrightarrow  3+2a>0\)

                      \(\Rightarrow |3+2a|=3+2a\)

Vì  \(b<0\Rightarrow |b|=-b\) 

Do đó: \(\dfrac{|3+2a|}{|b|}=\dfrac{3+2a}{-b} =-\dfrac{3+2a}{b}\).

Vậy \(\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=-\dfrac{3+2a}{b}\).

d) 

Ta có:

\((a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}=(a-b).\dfrac{\sqrt{ab}}{\sqrt{(a-b)^2}}\)

\(=(a-b).\dfrac{\sqrt{ab}}{|a-b|}\)

\(=(a-b).\dfrac{\sqrt{ab}}{-(a-b)}=-\sqrt{ab}\).

(Vì \(a < b < 0\) nên \(a-b<0\Rightarrow |a-b|=-(a-b)\) và \(ab>0).\)

Bài 35 trang 20 SGK Toán lớp 9 tập 1

Câu hỏi:

Tìm x biết:

a) \(\sqrt {{{\left( {x - 3} \right)}^2}}  = 9\)

b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1}  = 6\)

Lời giải:  

a) Ta có: 

\(\sqrt {{{\left( {x - 3} \right)}^2}}  = 9  \Leftrightarrow \left| {x - 3} \right| = 9\)

\( \Leftrightarrow \left[ \matrix{
x - 3 = 9 \hfill \cr 
x - 3 = - 9 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 9 + 3 \hfill \cr 
x = - 9 + 3 \hfill \cr} \right.\)

\( \Leftrightarrow \left[ \matrix{
x = 12 \hfill \cr 
x = - 6 \hfill \cr} \right.\)

Vậy phương trình đã cho có hai nghiệm: \(x = 12\) và \(x = -6\).

b) 

Ta có:

\(\sqrt{4x^2+4x+1}=6 \Leftrightarrow \sqrt{2^2x^2+4x+1}=6\)

\(\Leftrightarrow \sqrt{(2x)^2+2.2x+1^2}=6\)

\(\Leftrightarrow \sqrt{(2x+1)^2}=6\)

\(\Leftrightarrow |2x+1| =6\)

\(\eqalign{
& \Leftrightarrow \left[ \matrix{
2x + 1 = 6 \hfill \cr 
2x + 1 = - 6 \hfill \cr} \right. \cr 
& \Leftrightarrow \left[ \matrix{
2x = 6 - 1 \hfill \cr 
2x = - 6 - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
2x = 5 \hfill \cr 
2x = - 7 \hfill \cr} \right. \cr 
& \Leftrightarrow \left[ \matrix{
x = \dfrac{5}{2} \hfill \cr 
x = \dfrac{-7}{2} \hfill \cr} \right. \cr} \)

Vậy phương trình có \(2\) nghiệm \(x = \dfrac{5}{2}\) và \(x=\dfrac{-7}{2}\).

Bài 36 trang 20 SGK Toán lớp 9 tập 1

Câu hỏi:

Mỗi khẳng định sau đúng hay sai ? Vì sao ?

a) \(0,01 = \sqrt {0,0001} \);

b) \(- 0,5 = \sqrt { - 0,25} \);

c) \(\sqrt {39}  < 7\) và \(\sqrt {39}  > 6\);

d) \(\left( {4 - 13} \right).2{\rm{x}} < \sqrt 3 \left( {4 - \sqrt {13} } \right) \Leftrightarrow 2{\rm{x}} < \sqrt {3} \).

Phương pháp: 

+ \( \sqrt{A}\) xác định (hay có nghĩa) khi \(A \ge 0\).

+) Sử dụng định lí so sánh hai căn bậc hai:

              \(a < b \Leftrightarrow \sqrt{a} < \sqrt{b}\),   với \(a,\ b \ge 0\).

+ \(a.c >b.c \Leftrightarrow a> b\) , với \( c>0\).

Lời giải:  

a) Đúng. Vì \(\sqrt {0,0001}  = \sqrt {0,{{01}^2}}  = 0,01\)

Vì  \(VP=\sqrt{0,0001}=\sqrt{0,01^2}=0,01=VT\). 

b) Sai. 

Vì vế phải không có nghĩa do số âm không có căn bậc hai.

c) Đúng.

Vì: \(36 < 39 < 49\)  \(\Leftrightarrow \sqrt {36}  < \sqrt {39}  < \sqrt {49} \)

                                 \(\Leftrightarrow \sqrt {{6^2}}  < \sqrt {39}  < \sqrt {{7^2}} \)

                                 \(\Leftrightarrow 6 < \sqrt {39}  < 7\)

Hay \(\sqrt{39}>6\) và \( \sqrt{39} < 7\).

d) Đúng. 

Xét bất phương trình đề cho:

                  \((4-\sqrt{13}).2x<\sqrt 3 .(4-\sqrt{13})\)     \((1)\)

Ta có: 

\(16>13 \Leftrightarrow \sqrt{16} > \sqrt{13}\)

                       \(\Leftrightarrow \sqrt{4^2}> \sqrt{13}\)

                       \(\Leftrightarrow 4> \sqrt{13}\)

                       \(\Leftrightarrow 4-\sqrt{13}>0\)

Chia cả hai vế của bất đẳng thức \((1)\) cho số dương \((4-\sqrt{13})\), ta được:

                         \(\dfrac{(4-\sqrt{13}).2x}{(4-\sqrt{13})} <\dfrac{\sqrt 3 .(4-\sqrt{13})}{(4-\sqrt{13})}\)

                        \(\Leftrightarrow 2x < \sqrt 3.\)

 Vậy phép biến đổi tương đương trong câu d là đúng. 

Bài 37 trang 20 SGK Toán lớp 9 tập 1

Câu hỏi:

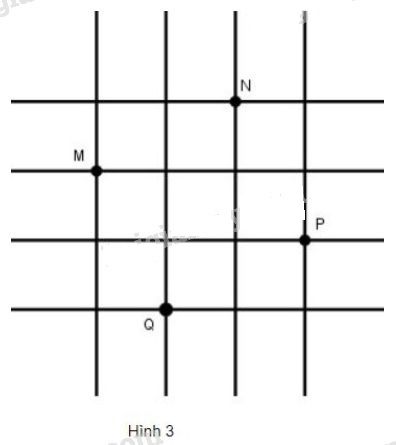
Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm (M, N, P, Q) (h.3).

Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.

Phương pháp: 

+ Sử dụng định lí Py-ta-go trong tam giác vuông.

+ Công thức tính diện tích hình vuông cạnh \(a\) là: \(S=a^2\).

+ Dấu hiệu nhận biết hình vuông: hình thoi có hai đường chéo bằng nhau (hay tứ giác có bốn cạnh bằng nhau và có hai đường chéo bằng nhau) thì là hình vuông.

Lời giải: 

Nối các điểm ta có tứ giác \(MNPQ\)

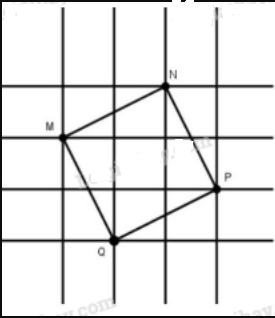
Tứ giác \(MNPQ\) có:

- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài \(2cm\), chiều rộng \(1cm\). Do đó theo định lí Py-ta-go, ta có:

\(MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm)\).

Hay \(MNPQ\) là hình thoi.

- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài \(3cm\), chiều rộng \(1cm\) nên theo định lý Py-ta-go ta có độ dài đường chéo là:

\(MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).\) 

Như vậy hình thoi \(MNPQ\) có hai đường chéo bằng nhau nên \(MNPQ\) là hình vuông.

Vậy diện tích hình vuông \(MNPQ\) bằng \(MN^{2}=(\sqrt{5})^{2}=5(cm^2)\).

Sachbaitap.com