Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 133 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số
Giải bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 133 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Bài tập ôn cuối năm - Phần đại số. Bài 17 Một lớp học có 40 học sinh được xếp ngồi đều nhau trên các ghế băng. Nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh. Tính số ghế băng lúc đầu.
Bài 9 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Giải các hệ phương trình:
a) \(\left\{ \matrix{2{\rm{x}} + 3\left| y \right| = 13 \hfill \cr 3{\rm{x}} - y = 3 \hfill \cr} \right.\)
b) \(\left\{ \matrix{3\sqrt x - 2\sqrt y = - 2 \hfill \cr 2\sqrt x + \sqrt y = 1 \hfill \cr} \right.\)
Lời giải:
a)
\(\left\{ \matrix{2{\rm{x}} + 3\left| y \right| = 13 \hfill \cr 3{\rm{x}} - y = 3 \hfill \cr} \right.\)
+) Trường hợp \(y ≥ 0\), ta có: \(\left| y \right| = y.\) Khi đó:
\(\begin{array}{l}
Hpt \Leftrightarrow \left\{ \begin{array}{l}
2x + 3y = 13\\
3x - y = 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
2x + 3\left( {3x - 3} \right) = 13
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
2x + 9x = 13 + 9
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
11x = 22
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
x = 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 3.2 - 3 = 3\;\;\left( {tm} \right)
\end{array} \right..
\end{array}\)
Vậy hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left( {2;\;3} \right).\)
+) Trường hợp \(y < 0\), ta có: \(\left| y \right| = -y.\) Khi đó:
\(\begin{array}{l}
Hpt \Leftrightarrow \left\{ \begin{array}{l}
2x - 3y = 13\\
3x - y = 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
2x - 3\left( {3x - 3} \right) = 13
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
2x - 9x = 13 - 9
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
- 7x = 4
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 3x - 3\\
x = - \dfrac{4}{7}
\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}
x = - \dfrac{4}{7}\\
y = 3.\left( { - \dfrac{4}{7}} \right) - 3 = - \dfrac{{33}}{7}\;\;\left( {tm} \right)
\end{array} \right..
\end{array}\)
Vậy hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left( {- \dfrac{4}{7};\;- \dfrac{33}{7}} \right).\)
Vậy phương trình có 2 cặp nghiệm: \((2; 3)\) và \(\displaystyle \left( { - {4 \over 7}; - {{33} \over 7}} \right)\)
b)
Điều kiện: \(x \geq 0\) và \(y \geq 0.\)
Đặt \(X = \sqrt x\) (với \(X ≥ 0\)); \(Y = \sqrt y\) (với \(Y ≥ 0\)). Khi đó
\(\begin{array}{l}
Hpt \Leftrightarrow \left\{ \begin{array}{l}
3X - 2Y = - 2\\
2X + Y = 1
\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}
Y = 1 - 2X\\
3X - 2\left( {1 - 2X} \right) = - 2
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
Y = 1 - 2X\\
3X - 2 + 4X = - 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
Y = 1 - 2X\\
7X = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
X = 0\;\left( {tm} \right)\\
Y = 1\;\;\left( {tm} \right)
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
\sqrt x = 0\\
\sqrt y = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 0\;\;\left( {tm} \right)\\
y = 1\;\;\left( {tm} \right)
\end{array} \right.
\end{array}\)
Vậy \((0; 1)\) là nghiệm của hệ phương trình.
Bài 10 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Giải các hệ phương trình:
a) \(\left\{ \matrix{2\sqrt {x - 1} - \sqrt {y - 1} = 1 \hfill \cr \sqrt {x - 1} + \sqrt {y - 1} = 2 \hfill \cr} \right.\)
b) \(\left\{ \matrix{{\left( {x - 1} \right)^2} - 2y = 2 \hfill \cr 3{\left( {x - 1} \right)^2} + 3y = 1 \hfill \cr} \right.\)
Lời giải:
a)
\(\left\{ \matrix{2\sqrt {x - 1} - \sqrt {y - 1} = 1 \hfill \cr \sqrt {x - 1} + \sqrt {y - 1} = 2 \hfill \cr} \right.\)
Điều kiện: \(x \geq 1\) và \(y \geq 1.\)
Đặt \(X = \sqrt {x - 1}\) (điều kiện \(X ≥ 0\))
\(Y = \sqrt {y - 1}\) (điều kiện \(Y ≥ 0\))
Hệ phương trình trở thành:
\(\eqalign{
& \left\{ \matrix{
2X - Y = 1 \hfill \cr
X + Y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
3{\rm{X}} = 3 \hfill \cr
X + Y = 2 \hfill \cr} \right.\cr& \Leftrightarrow \left\{ \matrix{
X = 1 \, \, (tm)\hfill \cr
Y = 1 \, \, (tm) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
\sqrt {x - 1} = 1 \hfill \cr
\sqrt {y - 1} = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x - 1 = 1 \hfill \cr
y - 1 = 1 \hfill \cr} \right.\cr& \Leftrightarrow \left\{ \matrix{
x = 2 \, \, (tm)\hfill \cr
y = 2 \, \, (tm)\hfill \cr} \right. \cr} \)
Vậy \((2;2)\) là nghiệm của hệ phương trình
b)
\(\left\{ \matrix{{\left( {x - 1} \right)^2} - 2y = 2 \hfill \cr 3{\left( {x - 1} \right)^2} + 3y = 1 \hfill \cr} \right.\)
Đặt \(X = (x – 1)^2\)(điều kiện \(X ≥ 0\)). Khi đó:
\(\begin{array}{l}
Hpt \Leftrightarrow \left\{ \begin{array}{l}
X - 2y = 2\\
3X + 3y = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
X = 2 + 2y\\
3\left( {2 + 2y} \right) + 3y = 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
X = 2 + 2y\\
6 + 6y + 3y = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
X = 2 + 2y\\
9y = - 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
X = 2 + 2y\\
y = - \dfrac{5}{9}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
X = \frac{8}{9}\;\;\left( {tm} \right)\\
y = - \frac{5}{9}
\end{array} \right.\\
\Rightarrow {\left( {x - 1} \right)^2} = \dfrac{8}{9} \Leftrightarrow \left[ \begin{array}{l}
x - 1 = \dfrac{{2\sqrt 2 }}{3}\\
x - 1 = - \dfrac{{2\sqrt 2 }}{3}
\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}
x = 1 + \dfrac{{2\sqrt 2 }}{3}\\
x = 1 - \dfrac{{2\sqrt 2 }}{3}
\end{array} \right..
\end{array}\)
Vậy hệ phương trình có hai nghiệm: \(\displaystyle \left( {1 + {{2\sqrt 2 } \over 3}; - {5 \over 9}} \right)\) và \(\displaystyle \left( {1 - {{2\sqrt 2 } \over 3}; - {5 \over 9}} \right)\)
Bài 11 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Hai giá sách có \(450\) cuốn. Nếu chuyển \(50\) cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ hai sẽ bằng \(\displaystyle {4 \over 5}\) số sách ở giá thứ nhất. Tính số sách lúc đầu trong mỗi giá.
Phương pháp:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng đã biết và các đại lượng chưa biết theo ẩn.
+) Dựa vào các dữ liệu của bài toán để lập phương trình hoặc hệ phương trình.
+) Giải phương trình hoặc hệ phương trình vừa lập tìm ẩn.
+) Đối chiếu với điều kiện của ẩn và kết luận theo yêu cầu của đề bài.
Lời giải:
Gọi \(x\) (cuốn) là số sách ở giá thứ nhất lúc ban đầu; \(y\) (cuốn) là số sách ở giá thứ hai lúc ban đầu. \(\left( {x,\;y \in N^*,\; 50 < x< 450}, \, \, y < 450\right)\)
Hai giá sách có \(450\) cuốn nên ta có: \(x+y=450.\)
Nếu chuyển \(50\) cuốn từ giá thứ nhất sang giá thứ hai thì số cuốn ở giá thứ nhất là \(x - 50\); số cuốn ở giá thứ hai là \(y + 50\). Khi đó, số sách ở giá thứ hai sẽ bằng \(\displaystyle {4 \over 5}\) số sách ở giá thứ nhất nên ta có: \(\displaystyle y + 50 = {4 \over 5}\left( {x - 50} \right)\)
Ta được hệ phương trình: \(\displaystyle \left\{ \matrix{x + y = 450 \hfill \cr y + 50 = {\displaystyle 4 \over \displaystyle 5}\left( {x - 50} \right) \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x + y = 450\\
\dfrac{4}{5}x - y = 90
\end{array} \right. \)
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
\dfrac{9}{5}x = 540\\
x + y = 450
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 300\\
300 + y = 450
\end{array} \right.
\end{array}\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = 300\;\;\left( {tm} \right)\\
y = 150\;\;\left( {tm} \right)
\end{array} \right..\)
Vậy số sách lúc đầu ở giá thứ I là \(300\) cuốn, ở giá thứ II là \(150\) cuốn.
Bài 12 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Quãng đường \(AB\) gồm một đoạn lên dốc dài \(4km\) và một đoạn xuống dốc dài \(5km\). Một người đi xe đạp từ \(A\) đến \(B\) hết \(40\) phút và đi từ \(B\) về \(A\) hết \(41\) phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Lời giải:
Phân tích:
|
|
Vận tốc lên dốc (km/h) |
Vận tốc xuống dốc (km/h) |
Thời gian lên dốc (giờ) |
Thời gian xuống dốc (giờ) |
Quãng đường lên dốc (km) |
Quãng đường xuống dốc (km) |
|
A đến B |
x |
y |
\(\frac{4}{x}\) |
\(\frac{5}{y}\) |
4 |
5 |
|
B về A |
x |
y |
\(\frac{5}{x}\) |
\(\frac{4}{y}\) |
5 |
4 |
Gọi vận tốc lúc lên dốc là \(x\left( {km/h} \right)\) và vận tốc lúc xuống dốc là \(y\left( {km/h} \right)\) \(\left( {x;y > 0} \right)\)
Thời gian lên dốc một đoạn \(4km\) là \(\dfrac{4}{x}\left( h \right)\), thời gian xuống dốc một đoạn \(5km\) là \(\dfrac{5}{y}\) (h)
Thời gian đi từ \(A\) đến \(B\) là tổng thời gian lên dốc đoạn \(4km\) và xuống dốc đoạn \(5km\) là \(40\)phút\( = \dfrac{2}{3}h\) nên ta có phương trình \(\dfrac{4}{x} + \dfrac{5}{y} = \dfrac{2}{3}\left( 1 \right)\)
Thời gian lên dốc một đoạn \(5km\) là \(\dfrac{5}{x}\left( h \right)\), thời gian xuống dốc một đoạn \(4km\) là \(\dfrac{4}{y}\) (h)
Thời gian đi từ \(B\) đến \(A\) là tổng thời gian lên dốc đoạn \(5km\) và xuống dốc đoạn \(4km\) là \(41\)phút\( = \dfrac{{41}}{{60}}h\) nên ta có phương trình \(\dfrac{5}{x} + \dfrac{4}{y} = \dfrac{{41}}{{60}}\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}\dfrac{4}{x} + \dfrac{5}{y} = \dfrac{2}{3}\\\dfrac{5}{x} + \dfrac{4}{y} = \dfrac{{41}}{{60}}\end{array} \right.\)
Đặt \(\left\{ \begin{array}{l}\dfrac{1}{x} = u\\\dfrac{1}{y} = v\end{array} \right.\,\left( {u;v \ne 0} \right)\) ta có hệ
\(\left\{ \begin{array}{l}4u + 5v = \dfrac{2}{3}\\5u + 4v = \dfrac{{41}}{{60}}\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}12u + 15v = 2\\300u + 240v = 41\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}192u + 240v = 32\\300u + 240v = 41\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}108u = 9\\12u + 15v = 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}u = \dfrac{1}{{12}}\\12.\dfrac{1}{{12}} + 15v = 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}u = \dfrac{1}{{12}}\\v = \dfrac{1}{{15}}\end{array} \right.\left( {TM} \right)\)
Thay lại cách đặt ta được \(\left\{ \begin{array}{l}u = \dfrac{1}{{12}}\\v = \dfrac{1}{{15}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{{12}}\\\dfrac{1}{y} = \dfrac{1}{{15}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 12\\y = 15\end{array} \right.\left( {TM} \right)\)
Vậy vận tốc khi xuống dốc là \(15km/h\) và vận tốc khi lên dốc là \(12km/h.\)
Bài 13 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Xác định hệ số \(a\) của hàm \(y = ax^2\), biết rằng đồ thị của nó đi qua điểm \(A(-2; 1)\). Vẽ đồ thị của hàm số đó.
Phương pháp:
+) Thay tọa độ của điểm A vào công thức hàm số để tìm a.
+) Lấy thêm 4 điểm bất kì thuộc đồ thị hàm số nữa để vẽ đồ thị hàm số.
Lời giải:
Gọi \((P)\) là đồ thị hàm số \(y = ax^2\)
Vì \(A(-2;1) \in(P)\): \(y = ax^2\) nên: \(\displaystyle 1 = a(-2)^2 ⇔ 4a = 1 ⇔ a = {1 \over 4}\)
Vậy ta có hàm số \(\displaystyle = {1 \over 4}{x^2}\)
* Vẽ đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}.\)
- Tập xác định \(D =R\)
- Bảng giá trị:
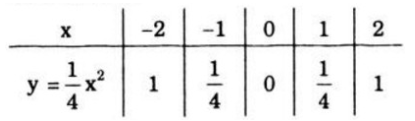
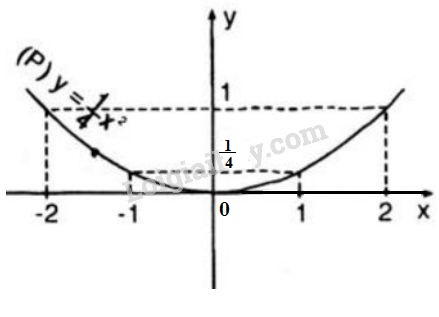
- Vẽ đồ thị:
Bài 14 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Gọi \({{\bf{x}}_{\bf{1}}},{\rm{ }}{{\bf{x}}_{\bf{2}}}\) là hai nghiệm của phương trình \({\bf{3}}{{\bf{x}}^{\bf{2}}}-{\rm{ }}{\bf{ax}}{\rm{ }}-{\rm{ }}{\bf{b}}{\rm{ }} = {\rm{ }}{\bf{0}}\). Tổng \({{\bf{x}}_{\bf{1}}} + {\rm{ }}{{\bf{x}}_{\bf{2}}}\) bằng:
(A) \(\displaystyle - {a \over 3}\) (B) \(\displaystyle {a \over 3}\) (C) \(\displaystyle {b \over 3}\) (D) \(\displaystyle - {b \over 3}\)
Hãy chọn câu trả lời đúng.
Lời giải:
Vì \(x_1\) và \(x_2\) là hai nghiệm của phương trình bậc hai một ẩn: \(\displaystyle 3{x^2} - ax + b = 0\)
Áp dụng hệ thức Vi-et, ta có: \( S = {x_1} + {x_2} ={a \over 3}\)
Chọn đáp án B
Bài 15 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Hai phương trình \({x^2} + ax + 1 = 0\) và \({x^2} - {\rm{ }}x{\rm{ }} - {\rm{ }}a{\rm{ }} = {\rm{ }}0\) có một nghiệm thực chung khi \(a\) bằng:
(A) 0 ; (B) 1 ; (C) 2 ; (D) 3
Hãy chọn câu trả lời đúng.
Lời giải:
Giả sử \(x_0\) là nghiệm chung của hai phương trình, thì \(x_0\) phải thỏa mãn:
\(\left\{ \matrix{x_0^2 + a{x_0} + 1 = 0 \, \, (1) \hfill \cr x_0^2 - {x_0} - a = 0 \, \, (2) \hfill \cr} \right.\)
Trừ vế với về của (1) cho (2), ta được:
\(ax_0+x_0+1+a=0\)
\(\begin{array}{l}
\Leftrightarrow \left( {a + 1} \right){x_0} + 1 + a = 0\\
\Leftrightarrow \left( {a + 1} \right)\left( {{x_0} + 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
a + 1 = 0\\
{x_0} + 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
a = - 1\\
{x_0} = - 1
\end{array} \right..
\end{array}\)
+) Thay \(a = -1\) vào (2), ta được: \(x_0^2 - {x_0} + 1 = 0\)
Ta có \( \Delta=-3<0\) nên phương trình vô nghiệm.
Vậy loại trường hợp \(a = -1.\)
+) Thay \(x_0 = -1\) vào (2), ta có \(1+1-a=0 \Leftrightarrow a=2.\)
Vậy hai phương trình đã cho có nghiệm chung \(x_0 = -1\) khi \(a=2.\)
Chọn đáp án C.
Bài 16 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Giải các phương trình:
a) \(2{x^3} - {\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\)
b) \(x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }} + {\rm{ }}4} \right)\left( {x{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}12.\)
Lời giải:
a)
\(\begin{array}{l}\;\;2{x^3} - {x^2} + 3x + 6 = 0\\\Leftrightarrow 2{x^3} + 2{x^2} - 3{x^2} + 6x - 3x + 6 = 0\\\Leftrightarrow 2{x^2}\left( {x + 1} \right) - 3x\left( {x + 1} \right) + 6\left( {x + 1} \right) = 0\\\Leftrightarrow \left( {x + 1} \right)\left( {2{x^2} - 3x + 6} \right) = 0\\\Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\2{x^2} - 3x + 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\2{x^2} - 3x + 6 = 0\;\;\left( * \right)\end{array} \right.\end{array}\)
Giải phương trình (*) ta có: \({\Delta = {{\left( { - 3} \right)}^2} - 4.2.6 = 9 - 48 =-39 < 0}\) nên phương trình (*) vô nghiệm.
Vậy phương trình có 1 nghiệm \(x = -1.\)
b)
\(\begin{array}{l}
\;x\left( {x + 1} \right)\left( {x + 4} \right)\left( {x + 5} \right) = 12\\
\Leftrightarrow \left[ {x\left( {x + 5} \right)} \right]\left[ {\left( {x + 1} \right)\left( {x + 4} \right)} \right] = 12\\
\Leftrightarrow \left( {{x^2} + 5x} \right)\left( {{x^2} + 5x + 4} \right) = 12 \, \, \, (*).
\end{array}\)
Đặt \({x^2} + 5x = t \Rightarrow {x^2} + 5x + 4 = t + 4.\)
Khi đó phương trình \(\left( * \right) \Leftrightarrow t\left( {t + 4} \right) = 12\)
\(\begin{array}{l}
\Leftrightarrow {t^2} + 4t - 12 = 0\\
\Leftrightarrow {t^2} + 6t - 2t - 12 = 0\\
\Leftrightarrow t\left( {t + 6} \right) - 2\left( {t + 6} \right) = 0\\
\Leftrightarrow \left( {t - 2} \right)\left( {t + 6} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
t - 2 = 0\\
t + 6 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
t = 2\\
t = - 6
\end{array} \right.\\
\Rightarrow \left[ \begin{array}{l}
{x^2} + 5x = 2\\
{x^2} + 5x = - 6
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
{x^2} + 5x - 2 = 0\;\;\;\;\left( 1 \right)\\
{x^2} + 5x + 6 = 0\;\;\;\left( 2 \right)
\end{array} \right.
\end{array}\)
+) Giải phương trình \((1)\) ta có: \(\Delta = {5^2} + 4.2 = 33 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt: \({x_1} = \dfrac{{ - 5 + \sqrt {33} }}{2}\) và \({x_2} = \dfrac{{ - 5 - \sqrt {33} }}{2}.\)
+) Giải phương trình \((2)\) ta có: \(\Delta = {5^2} - 4.6= 1 > 0 \Rightarrow \) phương trình có hai nghiệm phân biệt: \({x_1} = -2\) và \({x_2} = -3.\)
Vậy phương trình đã cho có bốn nghiệm
\(x=\dfrac{{ - 5 + \sqrt {33} }}{2};\) \(x=\dfrac{{ - 5 - \sqrt {33} }}{2};\) \(x=-2;x=-3.\)
Bài 17 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Một lớp học có 40 học sinh được xếp ngồi đều nhau trên các ghế băng. Nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh. Tính số ghế băng lúc đầu.
Lời giải:
Gọi \(x\) (chiếc) là số ghế băng lúc đầu. \((x \in N^*).\)
Khi đó số học sinh chia đều trên mỗi ghế băng là \(\displaystyle {{40} \over x}\) (học sinh)
Nếu bớt đi \(2\) ghế băng thì số ghế băng còn lại là \((x – 2)\) chiếc (x > 2). Khi đó mỗi ghế có \(\displaystyle \left( {{{40} \over x} + 1} \right)\) học sinh ngồi.
Vì tổng số học sinh vẫn là 40 em nên ta có phương trình:
\(\displaystyle \left( {x - 2} \right)\left( {{{40} \over x} + 1} \right) = 40\)
\(\Leftrightarrow 40 + x-\dfrac{80}{x}-2=40\)
\( \Leftrightarrow x-\dfrac {80}{x}-2=0\)\(\Rightarrow {x^2} - 2{\rm{x}} -80=0.\)
Có: \(\Delta' =1+80=81 >0 \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(x_1=10 \, \, (tm)\) và \(x_2=-8 \, (loại).\)
Vậy số ghế băng lúc đầu là \(10\) chiếc.
Bài 18 trang 133 SGK Toán lớp 9 tập 2
Câu hỏi:
Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.
Lời giải:
Gọi độ dài cạnh góc vuông ngắn hơn của tam giác đã cho là \(x \, (cm) \, \, (0< x < 10).\)
Khi đó cạnh góc vuông còn lại của tam giác là: \(x+2 \, (cm).\)
Áp dụng định lý Py-ta-go ta có: \( x^2+ (x+2)^2 = 10^2\)
\(\begin{array}{l}
\Leftrightarrow {x^2} + {x^2} + 4x + 4 = 100\\
\Leftrightarrow 2{x^2} + 4x - 96 = 0\\
\Leftrightarrow {x^2} + 2x - 48 = 0\\
\Leftrightarrow {x^2} + 8x - 6x - 48 = 0\\
\Leftrightarrow x\left( {x + 8} \right) - 6\left( {x + 8} \right) = 0\\
\Leftrightarrow \left( {x + 8} \right)\left( {x - 6} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 8 = 0\\
x - 6 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 8\;\;\left( {loại} \right)\\
x = 6\;\;\left( {tm} \right)
\end{array} \right..
\end{array}\)
Vậy hai cạnh góc vuông của tam giác vuông đó là \(6\, cm\) và \(8 \, cm.\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 135 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần hình học (09/06)
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 133 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 1, 2, 3, 4, 5, 6, 7, 8 trang 131, 132 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 38, 39, 40, 41, 42, 43, 44, 45 trang 129, 130, 131 SGK Toán 9 tập 2 - Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu (09/06)
- Bài 35, 36, 37 trang 126 SGK Toán 9 tập 2 - Luyện tập (02/06)
- Ôn tập cuối năm - Hình học
- Ôn tập cuối năm - Đại số
- Ôn tập chương IV Hình trụ - Hình nón – Hình cầu
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Chương IV. Hình Trụ - Hình Nón - Hình Cầu
- Ôn tập chương III Góc với đường tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
