Bài 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43 trang 93, 94, 95, 96 SGK Toán 9 tập 1 - Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông
Giải bài 33, 34 trang 93; bài 35, 36, 37 trang 94; bài 38, 39, 40 trang 95; bài 41, 42, 43 trang 96 sách giáo khoa Toán lớp 9 tập 1 bài Ôn tập chương I – Hệ thức lượng giác trong tam giác vuông. Bài 35 Tỉ số giữa hai cạnh góc vuông của một tam giác vuông bằng 19 : 28. Tìm các góc của nó
Bài 33 trang 93 SGK Toán lớp 9 tập 1
Câu hỏi:
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 41, sinα bằng
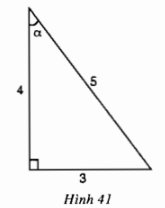
(A) \( \displaystyle{5 \over 3}\) (B) \( \displaystyle{5 \over 4}\) (C) \( \displaystyle{3 \over 5}\) (D) \( \displaystyle{3 \over 5}\)
b) Trong hình 42, sin Q bằng
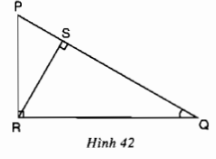
(A) \( \displaystyle{{P{\rm{R}}} \over {R{\rm{S}}}}\) (B) \( \displaystyle{{P{\rm{R}}} \over {QR}}\) (C) \( \displaystyle{{P{\rm{S}}} \over {S{\rm{R}}}}\) (D) \( \displaystyle{{S{\rm{R}}} \over {Q{\rm{R}}}}\)
c) Trong hình 43, cos 30° bằng
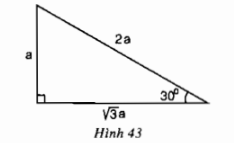
(A) \( \displaystyle{{2{\rm{a}}} \over {\sqrt 3 }}\) (B) \( \displaystyle{a \over {\sqrt 3 }}\) (C) \( \displaystyle{{\sqrt 3 } \over 2}\) (D) \( \displaystyle2\sqrt 3 {a^2}\)
Lời giải:
a)
Ta có: \( \displaystyle\sin \alpha = \dfrac{3}{5}.\)
Chọn (C)
b)
Xét \( \displaystyle\Delta QPR\) vuông tại R ta có: \( \displaystyle\sin Q = \dfrac{PR}{PQ}.\)
Xét \( \displaystyle\Delta RQS\) vuông tại S ta có: \( \displaystyle\sin Q = \dfrac{RS}{RQ}.\)
Chọn (D)
c) Chọn (C) vì: \( \displaystyle\cos {30^0} = {{\sqrt 3 a} \over {2a}} = {{\sqrt 3 } \over {2}}.\)
Bài 34 trang 93 SGK Toán lớp 9 tập 1
Câu hỏi:
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
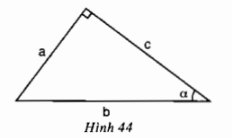
(A) \( \displaystyle \sin \alpha = {b \over c}\) (B) \( \displaystyle {\mathop{\rm cotg}\nolimits} \alpha = {b \over c}\)
(C) \( \displaystyle tg \alpha = {a \over c}\) (D) \( \displaystyle {\mathop{\rm cotg}\nolimits} \alpha = {a \over c}\)
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng?

(A) \( \displaystyle \sin^2 α + cos^2 α = 1\);
(B) \( \displaystyle \sin α = cos β\);
(C) \( \displaystyle \cos β = sin(90°- α)\);
(D) \( \displaystyle tg \alpha = {{\sin \alpha } \over {\cos \alpha }}\)
Lời giải:
a)
Áp dụng công thức lượng giác ta có:
\(\sin \alpha = \dfrac{a}{b};\;\;\cos\alpha = \dfrac{c}{b};\;\tan\alpha = \dfrac{a}{c};\;\;\cot\alpha = \dfrac{c}{a}.\)
Vậy C đúng.
Chọn C.
b)
Chọn C sai vì: \(\cosβ = \sin(90°-β)\) nên \(cos β = sin(90°- α)\) là sai, điều này chỉ đúng khi \( β = α=45^o.\)
Bài 35 trang 94 SGK Toán lớp 9 tập 1
Câu hỏi:
Tỉ số giữa hai cạnh góc vuông của một tam giác vuông bằng 19 : 28. Tìm các góc của nó.
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn: \(\tan \alpha = \dfrac{cạnh \, \, đối}{cạnh \, \, kề}.\)
Tổng hai góc nhọn trong tam giác vuông bằng \(90^o.\)
Lời giải:
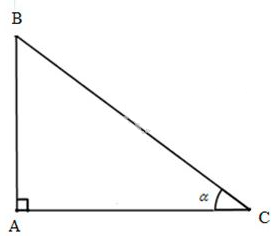
Giả sử tam giác \(ABC\) vuông tại \(A\) có \(AB:AC=19:28\). Ta đi tính góc B và góc C.
Xét tam giác \(ABC\) vuông tại \(A\), theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
\(\displaystyle \tan C ={{AB} \over {AC}}= {{19} \over {28}} \Rightarrow \widehat C \approx {34^0}10'\)
Vì tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B+\widehat C=90^0\) suy ra \(\widehat B=90^0-\widehat C=90° - 34°10’ = 55°50’\)
Vậy các góc nhọn của tam giác vuông đó có độ lớn là: \( 34°10’;\, \, 55°50’.\)
Bài 36 trang 94 SGK Toán lớp 9 tập 1
Câu hỏi:
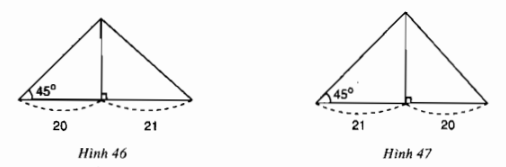
Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47)
Lời giải:
+) Xét hình 46, ta có:
\( BH < HC\,(20cm<21cm) ⇒ AB < AC\) (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn)
\(∆HAB\) vuông tại \(H\) có \(\widehat{ABH} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 20 \, (cm).\)
\(∆HAC\) vuông tại \(H,\) theo định lí Py-ta-go có:
\(AC^2=AH^2+HC^2=21^2+20^2=841=29^2.\)
\( \Rightarrow AC = \sqrt {{29^2}} = 29(cm)\)
Vậy cạnh lớn hơn là \(AC=29cm\)
+) Xét hình 47, ta có:
\( BH > HC\,(21cm>20cm) ⇒ AB > AC\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
\(∆ABH\) vuông tại \(H\) có \(\widehat{B} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 21 \, (cm)\)
Theo định lý Py-ta-go trong tam giác vuông \(ABH\) ta có:
\( AB = \sqrt {{{AH}^2} + {{BH}^2}}\)\(= \sqrt {{{21}^2} + {{21}^2}} = 21\sqrt 2 \approx 29,7(cm).\)
Vậy cạnh lớn hơn là \(AB=29,7cm\).
Bài 37 trang 94 SGK Toán lớp 9 tập 1
Câu hỏi:
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?
Phương pháp:
+) Chứng minh tam giác có tổng bình phương hai cạnh bằng bình phương cạnh còn lại thì tam giác đó là tam giác vuông.
+) Áp dụng tỉ số lượng giác của góc nhọn để tính các góc của tam giác ABC.
+) Áp dụng hệ thức lượng đối với tam giác vuông có đường cao để tính đường cao của tam giác đó.
+) Diện tích tam giác \(ABC\) vuông tại \(A\): \(S=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC.\)
Lời giải:
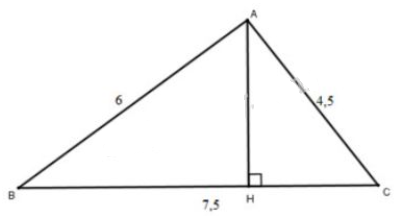
a) Xét ∆ABC có \(AB^2+AC^2={6^2} + 4,{5^2} = 36 + 20,25\)\( = 56,25 = 7,{5^2}=BC^2.\)
\(\Rightarrow ∆ABC\) vuông tại \(A\) (định lý Py-ta-go đảo).
\(\eqalign{&Ta \, \, có: tan B = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \Rightarrow \widehat C = {90^0} - \widehat B = {53^0}. \cr} \)
Áp dụng hệ thức lượng trong tam giác vuông ABC, có:
\(AH.BC = AB.AC\)
\( \displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm).\)
b)
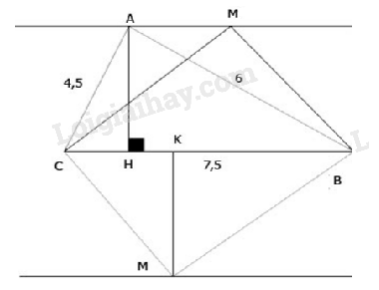
Kẻ \(MK \bot BC\) tại \(K.\)
Ta có: \(S_{ABC}=\dfrac{1}{2}AH.BC\)
\(S_{MBC}=\dfrac{1}{2}MK.BC\)
Từ đó, \( S_{ABC}=S_{MBC} \Leftrightarrow MK= AH=3,6cm.\)
Do đó \(M\) nằm trên hai đường thẳng song song cách \(BC\) một khoảng bằng \(3,6 cm\) (hình vẽ).
Bài 38 trang 95 SGK Toán lớp 9 tập 1
Câu hỏi:
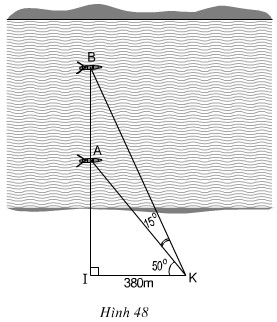
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)
Phương pháp:
+) Áp dụng: Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối.
Lời giải:
Ta có: \(\widehat {IKB} = {50^0} + {15^0} = {65^0}\)
\(∆IBK\) vuông tại \(I\) nên \(IB = IK. \tan \widehat{IKB} = 380 . tan 65° ≈ 814,9 (m).\)
\(∆IAK\) vuông tại \(I\) nên \(IA = IK.\tan \widehat{IKA} = 380 . tan 50° ≈ 452,9 (m).\)
Khoảng cách giữa hai thuyền là: \(AB = IB – IA ≈ 814,9 - 452,9 = 362 (m).\)
Bài 39 trang 95 SGK Toán lớp 9 tập 1
Câu hỏi:
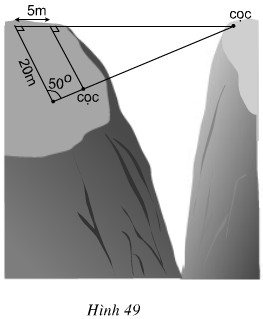
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
Phương pháp:
+) Áp dụng tính chất hai đường thẳng song song.
+) Dựa vào tỉ số lượng giác của góc nhọn.
Lời giải:
Giả sử hai cọc được đặt ở 2 điểm \(B\) và \(N\) trong hình vẽ.
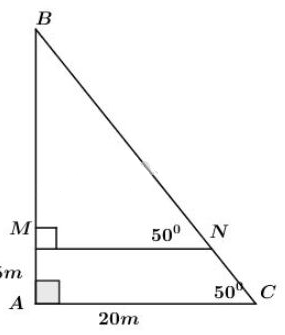
Ta có: \(MN// AC\) (vì cùng vuông với \(AB\)) \( \Rightarrow \widehat{BNM}=\widehat{BCA}=50^0\) (hai góc đồng vị).
Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan50^o = 20.\tan50^o.\)
\(\Rightarrow BM=AB-AM=20\tan50^o - 5 \approx 18,835 \,m.\)
Xét tam giác \(BMN\) vuông tại \(M\) ta có: \(\sin \widehat {BNM}=\dfrac {BM}{BN}\)\(\Rightarrow BN = \dfrac{{BM}}{{\sin 50^o}} = \dfrac{{18,835}}{{\sin 50^o}} \approx 24,59\;m.\)
Vậy khoảng cách giữa hai cọc là: \(BN \approx 24,59\;m.\)
Bài 40 trang 95 SGK Toán lớp 9 tập 1
Câu hỏi:
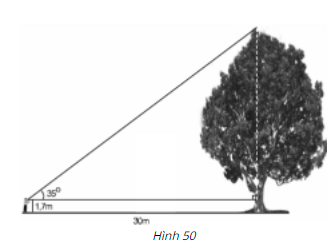
Tính chiều cao của cây trong hình 50 (làm tròn đến đề - xi – mét)
Phương pháp:
+) Chiều cao của cây bằng chiều cao của người quan sát + khoảng cách tử đỉnh đầu của người đó đến ngọn cây.
Lời giải:
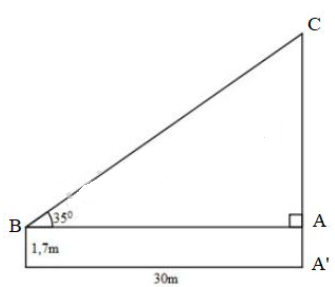
Xét tam giác vuông ABC vuông tại A ta có:
\(AC = AB.\tan {35^o} \approx 30.0,7 = 21\,m\)
Chiều cao của cây là:
\(A'C=AA' + AC≈ 1,7 + 21\)\(\, = 22,7 \,m=227\,dm.\)
Bài 41 trang 96 SGK Toán lớp 9 tập 1
Câu hỏi:
Tam giác ABC vuông tại \(C\) có \(AC = 2cm, BC = 5cm,\) \(\widehat {BAC} = x,\widehat {ABC} = y\). Dùng các thông tin sau (nếu cần) để tìm \(x – y\):
\(\sin 23°36’ ≈ 0,4;\)
\(\cos66°24’ ≈ 0,4;\)
\(tg21°48’ ≈ 0,4.\)
Phương pháp:
+) Dựa vào các tỉ số lượng giác của góc nhọn.
+) Tổng hai góc nhọn của tam giác bằng \(90^0.\)
Lời giải:
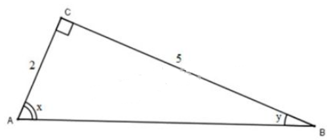
Xét tam giác ABC vuông tại C, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: \(\displaystyle \tan y =\dfrac{AC}{BC}= {2 \over 5} = 0,4\) nên \(y ≈ 21°48’.\)
Vì tam giác ABC vuông tại C nên \(x+y=90^0\) (tổng hai góc nhọn trong tam giác vuông).
Do đó: \(x = 90° - y ≈ 68°12’.\)
Vậy: \(x – y ≈ 68°12’ - 21°48’ ≈ 46°24’.\)
Bài 42 trang 96 SGK Toán lớp 9 tập 1
Câu hỏi:
Ở một cái thang dài \(3m\) người ta ghi: “ Để đảm bảo an toàn khi dùng thang phải đặt thang này tạo với mặt đất một góc có độ lớn từ \(60^0\) đến \(70^0\)”. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường bao nhiêu mét để đảm bảo an toàn?
Phương pháp:
+) Áp dụng tỉ số lượng giác của góc nhọn.
+) Hoặc: Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền nhân côsin góc kề.
Lời giải:
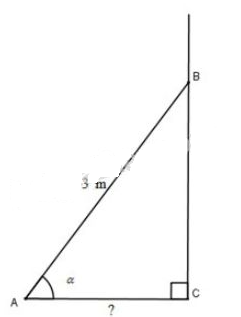
Kí kiệu như hình vẽ.
Cách 1:
Xét tam giác vuông \(ABC\) vuông tại \(C\). Ta có: \(AC=AB.\cos A\) (quan hệ giữa cạnh và góc trong tam giác vuông)
Vì \(60^0\le \widehat A \le 70^0\) nên ta xét:
+) Khi \(\widehat {CAB}=60^0\) thì \(AC = AB \cos A = 3\cos60^0 = 1,5 (m)\)
+) Khi \(\widehat {CAB}=70^0\) thì \(AC = AB\cos A = 3\cos70^0 ≈ 1,03 (m)\)
Vậy khi dùng thang đó, chân thang phải đặt cách tường một khoảng từ \(1,03m\) đến \(1,5m\) để đảm bảo an toàn.
Cách 2:
Vì \(60^0\le \widehat A \le 70^0\)
\(\Rightarrow \cos 70^o ≤ cosA ≤ \cos 60^o\)
\(\Rightarrow AB.\cos 70^o ≤ AB.cosA ≤ AB.\cos 60^o\)
\(\Rightarrow 3.\cos 70^o ≤ AB.cosA ≤ 3.\cos 60^o\)
\(\Rightarrow 1,03 ≤ AC ≤ 1,5\)
Vậy khi dùng thang đó, chân thang phải đặt cách tường một khoảng từ \(1,03m\) đến \(1,5m\) để đảm bảo an toàn.
Bài 43 trang 96 SGK Toán lớp 9 tập 1
Câu hỏi:
Đố:
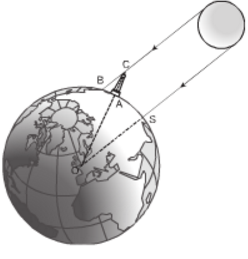
Vào khoảng năm 200 trước Công nguyên, Ơ-ra-tô-xten, một nhà Toán học và thiên văn học Hi Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau:
1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (Nay gọi là Át–xu-an), tức là tia sáng chiếu thẳng đứng.
2) Cùng lúc đó ở thành phố A-lếch-săng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m.
Từ hai quan sát trên, em hãy tính xấp xỉ “chu vi” Trái Đất.
(Trên hình 5, điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trung cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).
Phương pháp:
+) Áp dụng tỉ số lượng giác của góc nhọn.
Lời giải:
Bóng của tháp vuông góc với tháp:
\(∆ABC\) vuông tại \(A.\) Có \(AC=25m;AB=3,1m\) nên
\(\eqalign{
& tan C = {{AB} \over {AC}} = {{3,1} \over {25}} \approx 0,124 \cr
& \Rightarrow \widehat C = {7,07^0} \cr}\)
Các tia sáng được coi là song song với nhau hay \(BC//SO\) nên \(\widehat {SOA} =\widehat {ACB} = {7,07^0}\) (hai góc so le trong)
Vì Thành phố Xy-en nằm ở vị trí điểm S và thành phố A-lếch-xăng-đria nằm ở vị trí điểm A nên \(SA=800km\).
\(800km\) này được coi là ứng với độ dài cung có số đo là \(\widehat {SOA}=7,07^0\)
Mà số đo cả đường tròn (Trái Đất) là \(360^0\) nên chu vi của Trái Đất là: \(\displaystyle 800.{{360^0} \over 7,07^0} \approx 40735,5(km).\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 135 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần hình học (09/06)
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 133 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 1, 2, 3, 4, 5, 6, 7, 8 trang 131, 132 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 38, 39, 40, 41, 42, 43, 44, 45 trang 129, 130, 131 SGK Toán 9 tập 2 - Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu (09/06)
- Bài 35, 36, 37 trang 126 SGK Toán 9 tập 2 - Luyện tập (02/06)
- Ôn tập cuối năm - Hình học
- Ôn tập cuối năm - Đại số
- Ôn tập chương IV Hình trụ - Hình nón – Hình cầu
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Chương IV. Hình Trụ - Hình Nón - Hình Cầu
- Ôn tập chương III Góc với đường tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!