Bài 44, 45, 46, 47 trang 86 SGK Toán 9 tập 2 - Cung chứa góc
Giải bài 44, 45, 46, 47 trang 86 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Cung chứa góc. Bài 44 Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi
Bài 44 trang 86 SGK Toán lớp 9 tập 2
Câu hỏi:
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.
Lời giải:
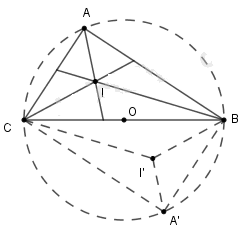
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận :
Điểm A luôn nhìn đoạn thẳng AB dưới một góc \(90^\circ \) nên quỹ tích điểm \(A\) là đường tròn đường kính \(BC.\)
Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \), lại có \(BI\) là phân giác góc \(B\) và \(CI\) là phân giác góc \(C\) nên
\(\widehat {ICB} = \dfrac{1}{2}\widehat {ACB};\,\widehat {IBC} = \dfrac{1}{2}\widehat {ABC} \Rightarrow \widehat {ICB} + \widehat {IBC} = \dfrac{1}{2}\left( {\widehat {ACB} + \widehat {ABC}} \right) = \dfrac{1}{2}.90^\circ = 45^\circ \)
Xét tam giác \(IBC\) có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \Leftrightarrow \widehat {BIC} = 180^\circ - 45^\circ = 135^\circ \)
Nên số đo góc \(BIC\) luôn không đổi.
Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc \(135^\circ .\)
Vậy điểm I thuộc hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.
Phần đảo:
Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của góc CBx
+ Kẻ tia Cy sao cho CI là phân giác của góc BCy
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
Ta có:
\(\begin{array}{l}
\widehat {BAC} = {180^0} - \left( {\widehat B + \widehat C} \right)\\
= {180^0} - 2\left( {\widehat {IBC} + \widehat {ICB}} \right)\\
= {180^0} - 2\left( {{{180}^0} - \widehat {BIC}} \right)\\
= {180^0} - {360^0} + {2.135^0}\\
= {90^0}
\end{array}\)
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận: Quĩ tích các điểm I là hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.
Bài 45 trang 86 SGK Toán lớp 9 tập 2
Câu hỏi:
Cho các hình thoi \(ABCD\) có cạnh \(AB\) cố định. Tìm quỹ tích giao điểm \(O\) của hai đường chéo của các hình thoi đó.
Lời giải:
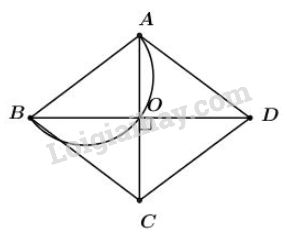
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh:
Phần thuận:
Vì ABCD là hình thoi nên \(AC \bot BD\) tại \(O.\) (Tính chất)
Vậy điểm \(O\) nhìn \(AB\) cố định dưới góc \(90^0.\)
\(\Rightarrow \) Quỹ tích điểm \(O\) là nửa đường tròn đường kính \(AB.\)
Phần đảo:
Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành (Dấu hiệu nhận biết)
Mà O thuộc nửa đường tròn đường kính AB
\(⇒ \widehat {AOB} = {90^0}\)
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi (Hình bình hành có 2 đường chéo vuông góc)
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
Bài 46 trang 86 SGK Toán lớp 9 tập 2
Câu hỏi:
Dựng một cung chứa góc \(55^0\) trên đoạn thẳng \(AB = 3cm.\)
Phương pháp:
Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)
Cách vẽ cung chứa góc \( \alpha\) dựng trên đoạn \(AB\).
+ Vẽ tia Ax tạo với AB một góc \( \alpha\)
+ Vẽ đường thẳng \( Ay \bot Ax\).
+ Vẽ đường trung trực d của đoạn thẳng AB. Gọi \( O\) là giao của \( Ay\) với \(d\).
+ Vẽ cung \(AmB\), tâm \(O\), bán kính \(OA\) sao cho cung này nằm ở nửa mặt phẳng bờ \(AB\) không chứa tia \(Ax\).
Cung \(AmB\) là một cung chứa góc \(\alpha\).
Lời giải:
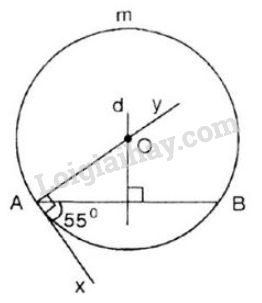
Cách dựng:
- Dựng đoạn thẳng \(AB = 3cm\) (dùng thước đo chia khoảng mm).
- Dựng góc \(\widehat{xAB} = 55^0\) (dùng thước đo góc và thước thẳng).
- Dựng tia \(Ay\) vuông góc với \(Ax\) (dùng êke).
- Dựng đường trung trực \(d\) của đoạn thẳng \(AB\) (dùng thước có chia khoảng và êke). Gọi \(O\) là giao điểm của \(d\) và \(Ay\).
- Dựng đường tròn tâm \(O,\) bán kính \(OA\) (dùng compa).
Ta có: \(\overparen{AmB}\) là cung chứa góc \(55^0\) dựng trên đoạn thẳng \(AB = 3cm\) (một cung).
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ Góc BAx là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈ cung AmB thì góc AMB là góc nội tiếp chắn cung nhỏ AB
\( \Rightarrow \widehat {BAx} = \widehat {AMB}\)(Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung)
\(\Rightarrow \widehat {AMB} = {55^0}\)
⇒ \(\overparen{AmB}\) là cung chứa góc 55º dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.
Bài 47 trang 86 SGK Toán lớp 9 tập 2
Câu hỏi:
Gọi cung chứa góc \(55^0\) ở bài tập 46 là \(\overparen{AmB}\). Lấy điểm \({M_1}\) nằm bên trong và điểm \({M_2}\) nằm bên ngoài đường tròn chứa cung này sao cho \({M_1},{M_2}\) và cung \(\overparen{AmB}\) nằm cùng về một phía đối với đường thẳng \(AB\). Chứng minh rằng:
a) \(\widehat {A{M_1}B} > 55^0\);
b) \(\widehat {A{M_2}B} < 55^0\).
Lời giải:
a) \({M_1}\) là điểm bất kì nằm trong cung chứa góc \(55^0\) (hình vẽ).
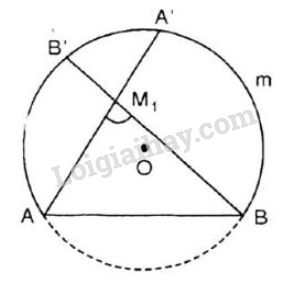
Gọi \(A', \, B’\) theo thứ tự là giao điểm của \({M_1}A,\) \({M_1}B\) với cung tròn.
Ta có \(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(\overparen{AB} = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))
Vì \(\widehat{A{M_1}B}\) là góc có đỉnh nằm trong đường tròn chắn cung \(A'B'\) và \(AB\) nên:
\(\widehat {A{M_1}B}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{A'B'}}{2}>\dfrac {1}{2}sđ\overparen{AB} =55^0\).
Vậy \(\widehat {A{M_1}B} > 55^0\)
b) \({M_2}\) là điểm bất kì nằm ngoài đường tròn (hình vẽ )
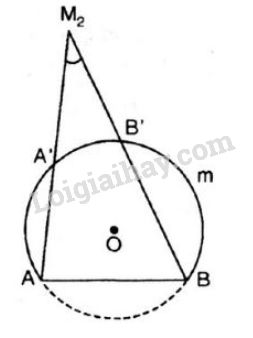
Ta có \({M_2}A, \, {M_2}B\) lần lượt cắt đường tròn tại \(A’, \, B’.\)
\(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(AB = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))
Vì góc \(\widehat {A{M_2}B}\) là góc có đỉnh nằm bên ngoài đường tròn chắn cung \(A'B'\) và \(AB\) nên:
\(\widehat {A{M_2}B}= \dfrac{sđ\overparen{AB}-sđ\overparen{A'B'}}{2}<\dfrac {1}{2}sđ\overparen{AB} =55^0 .\)
Vậy \(\widehat {A{M_2}B} < 55^0.\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 135 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần hình học (09/06)
- Bài 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 trang 133 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 1, 2, 3, 4, 5, 6, 7, 8 trang 131, 132 SGK Toán 9 tập 2 - Bài tập ôn cuối năm - Phần đại số (09/06)
- Bài 38, 39, 40, 41, 42, 43, 44, 45 trang 129, 130, 131 SGK Toán 9 tập 2 - Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu (09/06)
- Bài 35, 36, 37 trang 126 SGK Toán 9 tập 2 - Luyện tập (02/06)
- Ôn tập cuối năm - Hình học
- Ôn tập cuối năm - Đại số
- Ôn tập chương IV Hình trụ - Hình nón – Hình cầu
- Bài 3. Hình cầu. Diện tích hình cầu và thể tích hình cầu
- Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
- Chương IV. Hình Trụ - Hình Nón - Hình Cầu
- Ôn tập chương III Góc với đường tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
