Giải bài 1, 2, 3, 4, 5, 6 trang 117 SGK Toán 9 Cánh Diều tập 1
Biểu đồ hình quạt tròn ở Hình 64 mô tả các thành phần của một chai nước ép hoa quả (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn thành phần việt quất, táo, mật ong lần lượt có số đo là bao nhiêu độ.
Bài 1 trang 117 SGK Toán 9 tập 1 - Cánh Diều
Quan sát Hình 62, hãy cho biết:
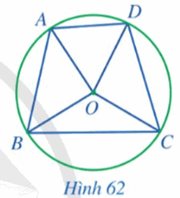
a) 6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm \(A,B,C,D\);
b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm.
Phương pháp:
Dựa vào định nghĩa góc ở tâm, góc nội tiếp để trả lời.
Lời giải:
a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D là các góc:
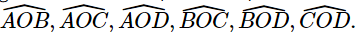
b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D là các góc:
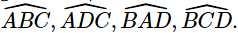
Bài 2 trang 117 SGK Toán 9 tập 1 - Cánh Diều
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) sao cho \(\widehat {AOB} = 90^\circ \). Giả sử \(M,N\) lần lượt là các điểm thuộc cung lớn \(AB\) và cung nhỏ \(AB\) (\(M,N\) khác \(A\) và \(B\)).
a) Tính độ dài đoạn thẳng \(AB\) theo \(R\).
b) Tính số đo các góc \(ANB\) và \(AMB\).
Phương pháp:
Dựa vào tính chất góc ở tâm và góc nội tiếp để tính.
Lời giải:
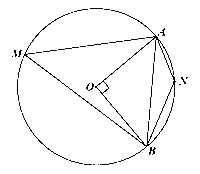
a) Xét đường tròn (O: R) có A, B thuộc đường tròn nên OA = OB = R.
Xét ∆AOB vuông tại O, theo định lí Pythagore, ta có:
AB2 = OA2 + OB2 = R2 + R2 = 2R2.
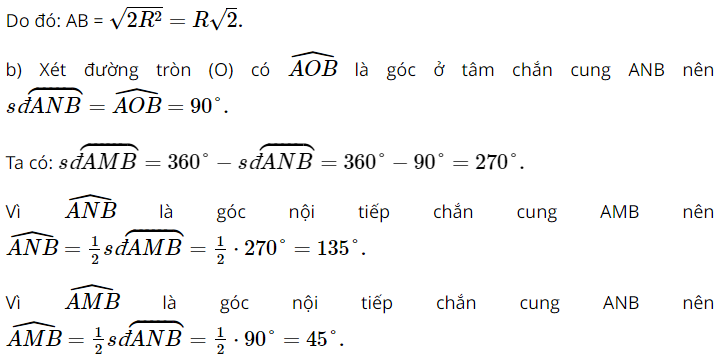
Bài 3 trang 117 SGK Toán 9 tập 1 - Cánh Diều
Trong Hình 63, cho biết \(AB = OA\).
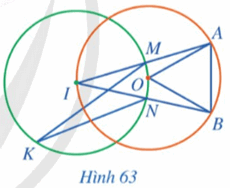
a) Tính số đo góc \(AOB\).
b) Tính số đo cung nhỏ \(AB\) và cung lớn \(AB\) của \(\left( O \right)\).
c) Tính số đo góc \(MIN\).
d) Tính số đo cung nhỏ \(MN\) và cung lớn \(MN\) của \(\left( I \right)\).
e) Tính số đo góc \(MKN\).
Phương pháp:
Dựa vào tính chất số đo góc ở tâm và số đo góc nội tiếp để chứng minh.
Lời giải:
a) Xét ∆OAB có OA = OB = AB nên ∆OAB là tam giác đều, do đó 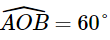
b) Số đo cung nhỏ AB là: 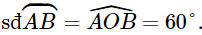
Số đo cung lớn AB (cung AIB) là: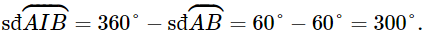
c) Góc MIN hay chính là góc AIB là góc nội tiếp chắn cung nhỏ AB nên 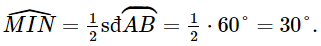
d) Xét đường tròn (I) có góc MIN là góc ở tâm chắn cung nhỏ MN (cung MON) nên số đo cung nhỏ MN là
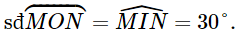
Số đo cung lớn MN (cung MKN) là:
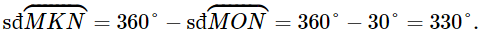
e) Xét đường tròn (I) có góc MKN là góc nội tiếp chắn cung nhỏ MN nên
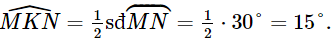
Bài 4 trang 117 SGK Toán 9 tập 1 - Cánh Diều
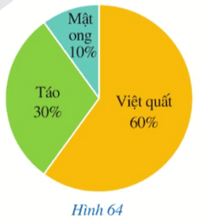
Biểu đồ hình quạt tròn ở Hình 64 mô tả các thành phần của một chai nước ép hoa quả (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn thành phần việt quất, táo, mật ong lần lượt có số đo là bao nhiêu độ.
Phương pháp:
Dựa vào tính chất số đo góc ở tâm để tính.
Lời giải:
Gọi các điểm A, B, C trên đường tròn (O) như hình vẽ.
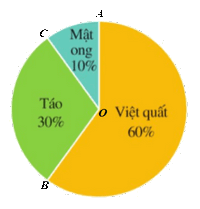
⦁ Do thành phần việt quất chiếm 60% thành phần nước ép hoa quả nên số đo cung nhỏ AB bằng 60% số đo của cung cả đường tròn. Vì thế, 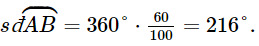
⦁ Do thành phần táo chiếm 30% thành phần nước ép hoa quả nên số đo cung nhỏ BC bằng 30% số đo của cung cả đường tròn. Vì thế, 
⦁ Do thành phần mật ong chiếm 10% thành phần nước ép hoa quả nên số đo cung nhỏ AC bằng 10% số đo của cung cả đường tròn. Vì thế, 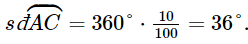
Bài 5 trang 117 SGK Toán 9 tập 1 - Cánh Diều
Cho hai đường tròn \(\left( O \right),\left( I \right)\) cắt nhau tại hai điểm \(A,B\). Kẻ các đoạn thẳng \(AC,AD\) lần lượt là đường kính của hai đường tròn \(\left( O \right),\left( I \right)\). Chứng minh ba điểm \(B,C,D\) thẳng hàng.
Phương pháp:
Dựa vào tính chất số đo góc nội tiếp để chứng minh.
Lời giải:
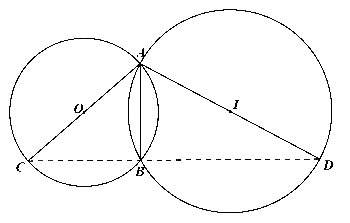
Ta có:
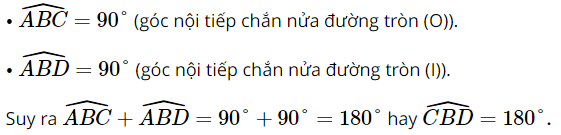
Do đó ba điểm B, C, D thẳng hàng.
Bài 6 trang 117 SGK Toán 9 tập 1 - Cánh Diều
Hãy sử dụng compa và thước thẳng để vẽ tam giác \(ABC\) vuông tại \(A\) và giải thích kết quả.
Phương pháp:
Dựa vào tính chất số đo góc ở tâm và số đo góc nội tiếp để chứng minh.
Lời giải:
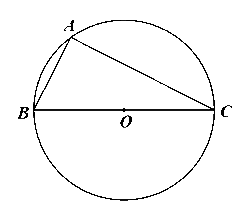
Bước 1. Vẽ đường tròn tâm O, kẻ đường kính BC.
Bước 2. Lấy điểm A thuộc đường tròn (O) (A khác B, C). Ta được tam giác ABC vuông tại A.
Thật vậy, xét đường tròn (O) có đường kính BC, điểm A thuộc (O) nên 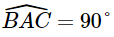
(góc nội tiếp chắn nửa đường tròn).
Vậy tam giác ABC vuông tại A.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 124, 125 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4 trang 122, 123 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5, 6 trang 117 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 109, 110 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 104 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Bài tập cuối chương 5
- Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
- Bài 4: Góc ở tâm. Góc nội tiếp
- Bài 3: Tiếp tuyến của đường tròn
- Bài 2: Vị trí tương đối của đường thẳng và đường tròn
- Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
- Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
