Giải SBT Toán 10 trang 70, 71, 72, 73 Kết nối tri thức tập 2

Bài 1 trang 70 SBT Toán 10 tập 2 Kết nối tri thức

Cho các mệnh đề:

P: “Phương trình bậc hai \(a{x^2} + bx + c\) có hai nghiệm phân biệt”;

Q: “Phương trình bậc hai \(a{x^2} + bx + c\) có biệt thức\(\Delta  = {b^2} - 4ac > 0\)”. 

a) Hãy phát biểu các mệnh đề: P => Q, Q => P, P ⇔ Q,  => . Xét tính đúng sai của các mệnh đề này.

b) Dùng các khái niệm "điều kiện cần” và "điều kiện đủ” để diễn tả mệnh đề  P => Q.

c) Gọi X là tập hợp các phương trình bậc hai \(a{x^2} + bx + c\) có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai \(a{x^2} + bx + c\) có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.

Lời giải:

a)               

+ Mệnh đề P => Q: Nếu phương trình bậc hai \(a{x^2} + bx + c\) có hai nghiệm phân biệt thì nó có biệt thức \(\Delta  = {b^2} - 4ac > 0\). Mệnh đề này đúng.

+ Mệnh đề Q => P: Nếu phương trình bậc hai \(a{x^2} + bx + c\) có biệt thức \(\Delta  = {b^2} - 4ac > 0\) thì nó có hai nghiệm phân biệt. Mệnh đề này đúng.

+ Mệnh đề P ⇔ Q: Phương trình bậc hai \(a{x^2} + bx + c\) có hai nghiệm phân biệt khi và chỉ khi nó có có biệt thức \(\Delta  = {b^2} - 4ac > 0\). Mệnh đề này đúng.

+ Mệnh đề : Phương trình bậc hai \(a{x^2} + bx + c\) không có hai nghiệm phân biệt thì nó có biệt thức \(\Delta  = {b^2} - 4ac > 0\). Mệnh đề này đúng.

b) + Phương trình bậc hai \(a{x^2} + bx + c\) có hai nghiệm phân biệt là điều kiện đủ để nó có biệt thức \(\Delta  = {b^2} - 4ac > 0\)

+ Phương trình bậc hai \(a{x^2} + bx + c\) có biệt thức \(\Delta  = {b^2} - 4ac > 0\) là điều kiện cần để nó có hai nghiệm phân biệt

c) Các phương trình bậc hai \(a{x^2} + bx + c\) có hệ số a và c trái dấu thì luôn có 2 nghiệm trái dấu.

 Vậy \(Y \subset X\)

Bài 2 trang 70 SBT Toán 10 tập 2 Kết nối tri thức

a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:

 \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x - 2y \ge  - 6\\2x + y \le 10\end{array} \right.\)

b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y)=2x +3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất)của F đạt được tại một trong các đỉnh của miền đa giác D.

Phương pháp:

- Xác định miền nghiệm của hệ bất phương trình (là một miền đa giác).

- Xác định tọa độ các đỉnh của đa giác.

- Tính giá trị của biểu thức f=2x+3y với (x,y) là tọa độ các đỉnh của đa giác sau đó so sánh để tìm ra giá trị nhỏ nhất.

Lời giải:

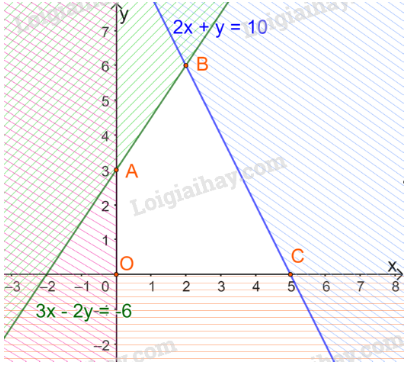
a)  - Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thoả mãn 1 > 0. Do đó miền nghiệm của bất phương trình  là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).

- Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thoả mãn 1> 0. Do đó miền nghiệm của bất phương trình  là nửa mặt phẳng bờ Ox chứa điểm  (0; 1) (miền không bị gạch).

- Bước 3: Vẽ đường thẳng : 3x - 2y = -6. Lấy điểm O(0;0) không thuộc , và thay x = 0, y = 0 vào biểu thức 3x - 2y ta được: 3.0 – 2.0 = 0>-6. Do đó miền nghiệm của bất phương trình 3x - 2y = -6 là nửa mặt phẳng bờ, chứa điểm O(0; 0) (miền không bị gạch).

- Bước 4: Vẽ đường thẳng : 2x + y = 10 và điểm O(0; 0) thoả mãn 2.0 + 0 =0 < 10. Do đó miền nghiệm của bất phương trình 2x + y = 10 là nửa mặt phẳng bờ  chứa điểm O(0, 0) (miền không bị gạch).

Vậy miền nghiệm D của hệ là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:

b) Ta có: F(0;0)=2.0 + 3.0= 0; F(0;3)=2.0 + 3.3= 9

F(2;6)=2.2 + 3.6= 22; F(5;0)=2.5 + 3.0= 10

Vậy trên miền D: giá trị lớn nhất của biểu thức F(x;y)=2x +3y là 22 và giá trị nhỏ nhất của biểu thức F(x;y)=2x +3y là 0.

Bài 3 trang 70 SBT Toán 10 tập 2 Kết nối tri thức

Cho tam thức bậc hai với đồ thị là parabol có đỉnh I(1, 4) và đi qua điểm A(2; 3)

a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).

b) Vẽ parabol này.

c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y =f(x).

d) Lập bảng xét dấu để giải bất phương trình \(\frac{{f(x)}}{{x - 2}} \ge 0\)

Lời giải:

a)  Parabol có đỉnh là I(1;4) nên phương trình có dạng \(y = a{(x - 1)^2} + 4\)

 Vì điểm A(2;3) thuộc parabol nên ta có:

\(3 = a{(2 - 1)^2} + 4 \Rightarrow a =  - 1\)

Vậy tam thức cần tìm là \(f(x) =  - {x^2} + 2x + 3\) ta có a= -1, b=2, c=3.

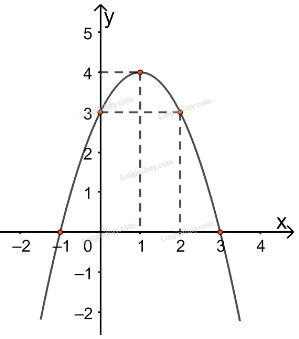
b) Ta có a= -1

   Đỉnh I(1;4), trục đối xứng x=1.

   Giao điểm của parabol với trục Oy là (0,3), với trục Ox là (-1,0) và (3,0)

c) Hàm số đồng biến trên khoảng (-∞;1) , nghịch biến trên khoảng (1,+∞)

Tập giá trị của hàm số là (-∞;4]

d) Xét bất phương trình \(\frac{{f(x)}}{{x - 2}} \ge 0\) hay  \(\frac{{ - {x^2} + 2x + 3}}{{x - 2}} \ge 0\)

\(f(x) =  - {x^2} + 2x + 3 = 0 \Leftrightarrow x =  - 1\) hoặc \(x = 3\)

\(x - 2 = 0 \Leftrightarrow x = 2\)

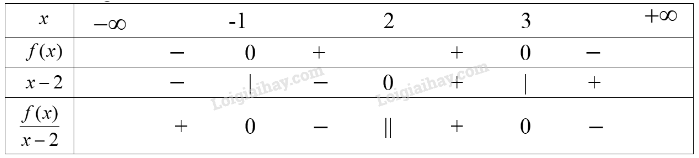
Ta có bảng xét dấu sau:

 Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ; - 1] \cup (2;3]\)

Bài 4 trang 71 SBT Toán 10 tập 2 Kết nối tri thức

Một quả bóng chày được đánh đi với vận tốc 35 m/s hợp với phương ngang một góc bằng 45° ở độ cao 1m so với mặt sân phẳng ở chỗ vụt bóng. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s.

a) Biết rằng quỹ đạo chuyển động của quả bóng chày được cho bởi phương trình:

\(y = \frac{{ - g}}{{2{v_o}^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha  + h\)

trong đó x là quãng đường (tính bằng mét) quả bóng bay được theo phương ngang, h là độ cao của quả bóng lúc được đánh đi so với mặt đất, vận tốc ban đầu \({v_o}\) hợp với phương ngang một góc \(\alpha \)

 Viết phương trình chuyển động của quả bóng chày.

 b) Tính độ cao lớn nhất của quả bóng chày. 

c) Tính tầm xa của quả bóng chày, tức là khoảng cách từ mặt đất ở chỗ đánh bóng và nơi quả bóng chạm đất (kết quả làm tròn đến hàng đơn vị).

 d) Có một hàng rào cao 4 m cách chỗ đánh bóng 125 m theo hướng đánh bóng. Hỏi quả bóng chày được đánh đi như trên có bị bay qua hàng rào đó hay không? 

Lời giải:

a)  Phương trình chuyển động của quả bóng chày là:

\(y = \frac{{ - 9,8}}{{{{2.35}^2}{{\cos }^2}{{45}^ \circ }}}{x^2} + x\tan {45^ \circ } + 1 = \frac{{ - 1}}{{125}}{x^2} + x + 1\)

b) Hàm số trên đạt giá trị lớn nhất tại \(x=\frac {-b}{2a} = 62,5 ,\, y(62,5) = 32, 25\)

Vậy độ cao cực đại của quả bóng là 32, 25m

c) Xét \(y = \frac{{ - 1}}{{125}}{x^2} + x + 1 = 0 \Leftrightarrow x \approx 126\) hoặc \(x \approx  - 1\) (loại)

Vậy tầm xa của quả bóng chày là khoảng 126m

d) Xét \(y = \frac{{ - 1}}{{125}}{x^2} + x + 1 < 4\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 125x + 375 > 0\\ \Leftrightarrow \left[ \begin{array}{l}x < 3\\x > 122\end{array} \right.\end{array}\)

Vậy quả bóng chày không bị bay qua hàng rào đó.

Bài 5 trang 71 SBT Toán 10 tập 2 Kết nối tri thức

Một công ty thời trang thấy rằng khi một loại áo phông được bán ở mức giá x (nghìn đồng) một chiếc thì số lượng áo phông bán được n cho bởi phương trình nhu cầu

n=21 000-150x 

a) Tìm công thức biểu diễn doanh thu R như là hàm của giá bán x. Tìm miền xác định của hàm số R = R (x). 

b) Giá bán nào sẽ làm cho doanh thu đạt cực đại? Tính doanh thu cực đại đó và số áo phông bán được trong trường hợp đó.

 c) Với giá bán như thế nào thì công ty sẽ đạt được ít nhất 675 triệu đồng doanh thu? 

Lời giải:

a) Công thức biểu diễn doanh thu R là:

\(R(x) = (21000 - 150x)x =  - 150{x^2} + 21000x\) (nghìn đồng)

Miền xác định của hàm số R(x) là D= [0;140]

b) R(x) đạt cực đại tại \(x =  - \frac{b}{{2a}} = 70\), thay vào R ta có R= 735 000

Vậy công ty bán với giá 70 nghìn đồng mỗi chiếc thì doanh thu đạt cực đại là 735 triệu đồng.

Số áo phông bán được trong trường hợp đó là:

n = 21 000 – 150 - 70 = 10 500 (chiếc).

c) Đổi: 675 triệu đồng = 675 000 nghìn đồng.

Xét bất phương trình  \( - 150{x^2} + 21000x \ge 675000\)

\( \Leftrightarrow  - 150{x^2} + 21000x - 675000 \ge 0 \Leftrightarrow 50 \le x \le 90\)

Vậy với giá bán từ 50 nghìn đồng đến 90 nghìn đồng mỗi chiếc thì công ty sẽ đạt được ít nhất 675 triệu đồng doanh thu.

Bài 6 trang 71 SBT Toán 10 tập 2 Kết nối tri thức

Người ta ước tính rằng trong khoảng từ năm 2010 đến năm 2030, số lượng điện thoại di động bán được của một công ty có thể được xấp xỉ bởi một hàm số bậc hai. Năm 2010 công ty đó bán được khoảng 19 nghìn chiếc điện thoại di động và năm 2019 bán được khoảng 100 nghìn chiếc điện thoại di động. Giả sử t là số năm tính từ năm 2010. Số điện thoại di động bán được năm 2010 được biểu diễn bởi điểm (0, 19) và số điện thoại di động bán được năm 2019 được biểu diễn bởi điểm (9, 100). Giả sử điểm (0;19) là đỉnh đồ thị của hàm số bậc hai này. 

a) Tìm hàm số bậc hai biểu diễn số điện thoại di động công ty đó bản được qua từng năm.

 b) Dựa trên mô hình này, hãy tính số điện thoại di động bán được năm 2024.

c) Dựa trên mô hình này, hãy ước lượng xem khi nào thì số điện thoại di động bán được được vượt mức 300 nghìn chiếc.

Lời giải:

a)  Giả sử \(y = a{t^2} + bt + c\;(a \ne 0)\) là hàm số mô tả số lượng điện thoại di động bán được qua từng năm, trong đó t là số năm tính từ năm 2010.

Có (0; 19) là đỉnh của đồ thị hàm số nên b = 0 và c = 19.

Điểm (9; 100) thuộc đồ thị hàm số nên ta có:

\(100 = a{.9^2} + 19 \Leftrightarrow 81a - 81 = 0 \Leftrightarrow a = 1.\)

Vậy hàm số cần tìm là: \(y = {t^2} + 19\)

b) Năm 2024 tương ứng với t = 14.

Số lượng điện thoại di động bán được trong năm 2024 là:

\(y = {14^2} + 19 = 215\) (nghìn chiếc).

c) Xét bất phương trình \({t^2} + 19 > 300\)

\( \Leftrightarrow {t^2} - 281 > 0 \Rightarrow t > 16,8\)

Vậy từ năm 2027 trở đi (đến năm 2030) thì số điện thoại di động bán được được vượt mức 300 nghìn chiếc.

Bài 7 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Tìm các giá trị của tham số m để hàm số \(\sqrt {{x^2} + 2mx - 2m + 3} \)  có tập xác định là toàn bộ tập số thực R.

 Lời giải:

 Hàm số đã cho có tập xác định là R khi và chỉ khi \({x^2} + 2mx - 2m + 3 \ge 0\)  với mọi \(x \in \mathbb{R}\)

Xét \(f(x) = {x^2} + 2mx - 2m + 3\) có \(\Delta ' = {m^2} + 2m - 3\) và \(a = 1 > 0\)

Ta có \(f(x) \ge 0\forall x \in R \Leftrightarrow \Delta ' \le 0\)

\( \Leftrightarrow {m^2} + 2m - 3 \le 0 \Leftrightarrow (m + 3)(m - 1) \le 0 \Leftrightarrow  - 3 \le m \le 1\)

Vậy \(m \in [-3;1]\) thì hàm số có tập xác định là \(\mathbb R\)

Bài 8 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Giải các phương trình chứa căn thức sau: 

a) \(\sqrt {3{x^2} - 4x + 1}  = \sqrt {{x^2} - x} \)

b) \(\sqrt {6{x^2} - 11x - 3}  = 2x - 1\)

Phương pháp:

Bước 1: Bình phương hai vế của PT

Bước 2: Giải PT thu được

Bước 3: Thử lại và KL nghiệm

Lời giải:

a) \(\sqrt {3{x^2} - 4x + 1}  = \sqrt {{x^2} - x} \)

\(\begin{array}{l} \Rightarrow 3{x^2} - 4x + 1 = {x^2} - x\\ \Leftrightarrow 2{x^2} - 3x + 1 = 0\\ \Leftrightarrow (x - 1)(2x - 1) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{1}{2}\end{array} \right.\end{array}\)

Thử lại ta thấy PT đã cho có nghiệm duy nhất \(x = 1\)

b) \(\sqrt {6{x^2} - 11x - 3}  = 2x - 1\)

\(\begin{array}{l} \Rightarrow 6{x^2} - 11x - 3 = {\left( {2x - 1} \right)^2}\\ \Leftrightarrow 6{x^2} - 11x - 3 = 4{x^2} - 4x + 1\\ \Leftrightarrow 2{x^2} - 7x - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - \frac{1}{2}\end{array} \right.\end{array}\)

Thử lại ta thấy PT đã cho có nghiệm duy nhất \(x = 4\)

Bài 9 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Đội văn nghệ của một trường trung học phổ thông gồm có 5 học sinh khối lớp 10, 5 học sinh khối lớp 11 và 5 học sinh khối lớp 12. Nhà trường cần chọn một đội gồm 10 học sinh để tham gia thi văn nghệ cấp huyện. Tính số cách lập đội văn nghệ sao cho có học sinh ở cả ba khối lớp và có nhiều nhất 2 học sinh khối lớp 10. 

Lời giải:

 Đội văn nghệ có học sinh ở cả ba khối lớp và có nhiều nhất 2 học sinh khối lớp 10 nên ta có 2 phương án:

- Phương án 1: Có 1 học sinh khối lớp 10

 Chọn ra 1 học sinh lớp 10 từ 5 học sinh có 5 cách

 Chọn ra 9 học sinh từ 2 khối 11 và 12 có \(C_{10}^9 = 10\)cách

- Phương án 1: Có 2 học sinh khối lớp 10

 Chọn ra 2 học sinh lớp 10 từ 5 học sinh có \(C_5^2 = 10\) cách

 Chọn ra 9 học sinh từ 2 khối 11 và 12 có \(C_{10}^8 = 45\)cách

Vậy có tổng số cách chọn theo yêu cầu là 5. 10+ 10. 45= 500 cách.

Bài 10 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Viết khai triển nhị thức Newton của \({(3x - 2)^n}\), biết n là số tự nhiên thoả mãn \(A_n^2 + 2C_n^1 = 30\)

Phương pháp:

 Áp dụng công thức \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)

Lời giải:

Ta có \(A_n^2 + 2C_n^1 = 30 \Leftrightarrow \frac{{n!}}{{(n - 2)!}} + 2\frac{{n!}}{{1!(n - 1)!}} = 30\)

\(\begin{array}{l} \Leftrightarrow n(n - 1) + 2n - 30 = 0\\ \Leftrightarrow {n^2} + n - 30 = 0\end{array}\)

\( \Leftrightarrow n = 5\) (thỏa mãn) hoặc \(n =  - 6\) (loại)

Khi đó \(\begin{array}{l}{(3x - 2)^n} = {(3x - 2)^5}\\ = {(3x)^5} + 5{(3x)^4}.( - 2) + 10{(3x)^3}{( - 2)^2} + 10{(3x)^2}{( - 2)^3} + 5.3x{( - 2)^4} + {( - 2)^5}\\ = 243{x^5} - 810{x^4} + 1080{x^3} - 720{x^2} + 240x - 32\end{array}\)

Bài 11 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Cho tam giác ABC có AB =2, AC = 3, BC = 4.

a) Tính diện tích S của tam giác.

b) Tính bán kính đường tròn ngoại tiếp của tam giác. 

Lời giải:

a) Ta có: \(p = \frac{{a + b + c}}{2} = \frac{{4 + 3 + 2}}{2} = \frac{9}{2}\)

\( \Rightarrow S = \sqrt {p(p - a)(p - b)(p - c)}  = \sqrt {\frac{9}{2}\left( {\frac{9}{2} - 4} \right)\left( {\frac{9}{2} - 3} \right)\left( {\frac{9}{2} - 2} \right)}  = \frac{{3\sqrt {15} }}{4}\)

b) Gọi R là bán kính đường tròn ngoại tiếp của tam giác ABC. Ta có:

\(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.3.2}}{{4.\frac{{3\sqrt {15} }}{4}}} = \frac{{8\sqrt {15} }}{{15}}\)

Bài 12 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD của tam giác OAB (D thuộc đoạn AB). 

a) Tính OA, OB,

b) Chứng minh rằng  \(\overrightarrow {OD}  = \frac{2}{3}\overrightarrow {OA}  + \frac{1}{3}\overrightarrow {OB} \)

c) Tìm toạ độ điểm D.  

Lời giải:

a) Ta có \(OA = \sqrt {{3^2} + {4^2}}  = 5;OB = \sqrt {{8^2} + {6^2}}  = 10\)

b) Theo tính chất đường phân giác ta có:

\(\frac{{AD}}{{BD}} = \frac{{OA}}{{OB}} = \frac{5}{{10}} = \frac{1}{2} \Rightarrow BD = 2AD\)

Do D thuộc AB nên \(\overrightarrow {AD} \)  và \(\overrightarrow {BD} \) ngược hướng.

\(\begin{array}{l} \Rightarrow \overrightarrow {BD}  =  - 2\overrightarrow {AD} \\ \Leftrightarrow \overrightarrow {OD}  - \overrightarrow {OB}  =  - 2\left( {\overrightarrow {OD}  - \overrightarrow {OA} } \right)\\ \Leftrightarrow 3\overrightarrow {OD}  = \overrightarrow {OB}  + 2\overrightarrow {OA} \\ \Leftrightarrow \overrightarrow {OD}  = \frac{1}{3}\overrightarrow {OB}  + \frac{2}{3}\overrightarrow {OA} \end{array}\)

c) Gọi \(D({x_o};{y_o})\) từ b suy ra \(\;\left\{ \begin{array}{l}{x_o} = \frac{2}{3}{x_A} + \frac{1}{3}{x_B} = \frac{{14}}{3}\\{y_o} = \frac{2}{3}{y_A} + \frac{1}{3}{y_B} = \frac{{14}}{3}\end{array} \right.\)

Vậy \(D\left( {\frac{{14}}{3};\frac{{14}}{3}} \right)\)

Bài 13 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm của các đoạn thẳng BC, AC, AB. Biết rằng M( 1; 2), N(O; -1) và P(-2; 3). 

a) Lập phương trình tham số của đường thẳng BC.

b) Lập phương trình tổng quát của đường trung trực của đoạn thẳng BC

Lời giải:

a)  Xét tam giác ABC có:

  P, N là trung điểm của AB, Ac

=> PN // BC

\( \Rightarrow \overrightarrow {{u_{BC}}}  = \frac{1}{2}\overrightarrow {PN}  = (1; - 2)\) là vectơ chỉ phương của BC

 Có BC đi qua M(1;2) nên BC có phương trình tham số là:

\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 - 2t\end{array} \right.\)

 b) Gọi \(\Delta \) là đường trung trực của BC.

 - \(\Delta \) đi qua điểm M(1,2) là trung điểm BC

 - \(\Delta \) vuông góc với BC nên \(\overrightarrow {{n_\Delta }}  = \overrightarrow {{u_{BC}}}  = (1; - 2)\) là vectơ pháp tuyến của \(\Delta \)

Vậy phương trình tổng quát của \(\Delta \) là: 1(x-1)- 2(y-2)=0 <=> x-2y+3=0

Bài 14 trang 72 SBT Toán 10 tập 2 Kết nối tri thức

Cho đường thẳng: \(\Delta :3x + 4y - 25 = 0\). Gọi (C) là đường tròn tâm O và tiếp xúc với \(\Delta \).

a) Viết phương trình đường tròn (C) 

b) Tìm toạ độ tiếp điểm H của \(\Delta \) và (C).

Lời giải:

a) Bán kính của (C) bằng: \(R = d(O,\Delta ) = \frac{{\left| {3.0 + 4.0 - 25} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 5\)

Vậy phương trình đường tròn (C) tâm O(0;0) bán kính R=5 là \({x^2} + {y^2} = 25\)

b) Ta có: \(\Delta \) tiếp xúc (C) tại điểm H

\(\begin{array}{l} \Rightarrow OH \bot \Delta \\ \Rightarrow \overrightarrow {{u_{OH}}}  = \overrightarrow {{n_\Delta }}  = (3;4)\\ \Rightarrow \overrightarrow {{n_{OH}}}  = ( - 4;3)\end{array}\)

=> Phương trình đường thẳng OH là 4x- 3y= 0

Ta có \(H = OH \cap \Delta \), do đó tọa độ H là nghiệm của hệ

\(\left\{ \begin{array}{l}3x + 4y - 25 = 0\\4x - 3y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 4\end{array} \right.\)

Vậy H(3,4).

Bài 15 trang 73 SBT Toán 10 tập 2 Kết nối tri thức

Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng toạ độ. Theo đó, tại thời điểm \(t(0 \le t \le 180)\), vật thể có vị trí toạ độ \(\left( {4\cos t^\circ ;{\rm{ }}3\sin t^\circ } \right)\). 

a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.

b) Tìm quỹ đạo chuyển động của vật thể.

Lời giải:

a) Vị trí ban đầu của vật thể ứng với t = 0 => Vật thể ở vị trí có toạ độ là \({A_1} = \left( {4\cos 0^\circ ;{\rm{ }}3\sin 0^\circ } \right) = \left( {4;0} \right).\)

Vị trí kết thúc của vật thể ứng với t = 180 => Vật thể ở vị trí có toạ độ là \({A_2} = \left( {4\cos {{180}^ \circ };{\rm{ }}3\sin {{180}^ \circ }} \right) = \left( { - 4;0} \right).\)

b) Từ đẳng thức \(\left( {4\cos t^\circ ;{\rm{ }}3\sin t^\circ } \right)\) là toạ độ của vật thể M, ta có \({\left( {\frac{{{y_M}}}{3}} \right)^2} + {\left( {\frac{{{x_M}}}{4}} \right)^2} = 1 \Leftrightarrow \frac{{x_M^2}}{{16}} + \frac{{y_M^2}}{9} = 1\)

Do đó vật thể chuyển động trên đường elip (E) có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)

Khi thay đổi trên đoạn [0; 180] thì sin t° thay đổi trên đoạn [0; 1] và cos t° thay đổi trên đoạn [-1; 1].

 \( \Rightarrow 4\cos t^\circ  \in \;\left[ { - 4;4} \right]\) và \(3\sin t^\circ  \in \;\left[ {0;{\rm{ }}3} \right].\)

Vậy quỹ đạo của vật thể (hay là tập hợp điểm M) là nửa đường elip (E) nằm trên trục hoành.

Bài 16 trang 73 SBT Toán 10 tập 2 Kết nối tri thức

Bảng sau đây cho biết lượng mưa trung bình hằng tháng tại Đà Nẵng và Hà Nội (mm).

 (Theo WWW.Weatherspark.com) 

a) Đà Nẵng hay Hà Nội có lượng mưa trung bình cả năm cao hơn? 

b) Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của hai mẫu số liệu về lượng mưa trung bình các tháng tại Đà Nẵng và Hà Nội. Nhận xét gì về sự phân tán của hai mẫu số liệu này? 

Lời giải:

a) Lượng mưa trung bình cả năm của Đà Nẵng là  \(\overline x  = \frac{{39,5 + 13,2 + ... + 145,1}}{{12}} \approx 115,79\)

Lượng mưa trung bình cả năm của Hà Nội là \(\overline y  = \frac{{13,0 + 11,9 + ... + 14,1}}{{12}} \approx 95,08\)

Vậy Đà Nẵng có lượng mưa trung bình cả năm cao hơn Hà Nội.

 b) Khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của hai mẫu số liệu là:

+ Đà Nẵng:

Sắp xếp lượng mưa trung bình hàng tháng theo thứ tự tăng dần, ta được:

Khoảng biến thiên\(\;{R_1} = 304,0 - 13,2 = 290,8\)

Trung vị \({Q_2} = \frac{1}{2}\left( {60,2 + 62,5} \right) = 61,35\)

Tứ phân vị thứ nhất \({Q_1} = \frac{1}{2}\left( {28 + 39,5} \right) = 33,75\)

Tứ phân vị thứ ba \({Q_3} = \frac{1}{2}\left( {145,1 + 253,5} \right) = 199,25\)

Khoảng tứ phân vị \({\Delta _Q} = 199,25 - 33,75 = 165,5\)

Phương sai: \({s_1}^2 = \frac{{{{\left( {13,2 - 115,79} \right)}^2} + ... + {{\left( {304,0 - 115,79} \right)}^2}}}{{12}} \approx 10801,9074\)

Độ lệch chuẩn \({s_1} = \sqrt {{s_1}^2}  = \sqrt {10801,9074}  \approx 103,93\)

 + Hà Nội:

Sắp xếp lượng mưa trung bình hàng tháng theo thứ tự tăng dần, ta được:

Khoảng biến thiên\(\;{R_2} = 226,2 - 11,9 = 214,3\)

Trung vị \({Q_2}' = \frac{1}{2}(52,5 + 84,8) = 68,65\)

Tứ phân vị thứ nhất \({Q_1}' = \frac{1}{2}\left( {14,1 + 29,2} \right) = 21,65\)

Tứ phân vị thứ ba \({Q_3}' = \frac{1}{2}\left( {160,1 + 173,8} \right) = 166,95\)

Khoảng tứ phân vị \({\Delta _Q}' = 166,95 - 21,65 = 145,3\)

Phương sai: \({s_2}^2 = \frac{{{{\left( {11,9 - 95,08} \right)}^2} + ... + {{\left( {226,2 - 95,08} \right)}^2}}}{{12}} \approx 5786,322\)

Độ lệch chuẩn \({s_2} = \sqrt {{s_2}^2}  = \sqrt {5786,322}  \approx 76,07\)

So sánh: \({R_1} > {R_2};{\Delta _Q} > \Delta {'_Q};{s_1} > {s_2}\)

Kết luận: Dãy số liệu về lượng mưa trung bình của các tháng tại Đà Nẵng phân tán hơn so với tại Hà Nội.

Bài 17 trang 73 SBT Toán 10 tập 2 Kết nối tri thức

Khi tham gia một trò chơi quay số trúng thưởng, mỗi người chơi chọn một số 4 chữ số (có tính cả số 0 ở đầu). Bạn An chọn số 0347. Người quản trò quay 4 tấm bìa cứng hình tròn I, II, III, IV, mỗi tấm bìa được chia thành 10 phần có diện tích bằng nhau và đánh số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 được gắn vào trục quay có mũi tên ở tâm. Giả sử mũi tên của bìa cứng số I, II, III và IV tương ứng dừng ở các số a, b, c, d. Khi đó số abcd gọi là số trúng thưởng. Nếu số của người chơi trung hoàn toàn với số trúng thưởng thì người chơi trúng giải nhất trùng với 3 chữ số của số trúng thưởng (tính cả thứ tự) thì người chơi trúng giải nhì.

Tính xác suất bạn An trúng giải nhất, giải nhì. 

Lời giải:

Không gian mẫu \(\Omega  = \{ \overline {abcd} ;a,b,c,d \in \{ 0;1;2;3;4;5;6;7;8;9\} \} \)

Mỗi chữ số có 10 cách chọn.

Theo quy tắc nhân ta có: \(n(\Omega ) = {10^4}\)

Gọi E là biến cố “An trúng giải nhất”.

\(E = \left\{ {0347} \right\} \Rightarrow n\left( E \right) = 1\)

\( \Rightarrow P(E) = \frac{1}{{{{10}^4}}} = 0,0001\)

Gọi F là biến cố “An trúng giải nhì” \(F = \{ a347;0b47;03c7;034d\} \)

Trong đó \(a,b,c,d \in \{ 0;1;2;3;4;5;6;7;8;9\} \)

\( \Rightarrow n\left( F \right){\rm{ =  }}9.{\rm{ }}4 = {\rm{ }}36\)

\( \Rightarrow P(F) = \frac{{36}}{{{{10}^4}}} = 0,0036\)

Vậy xác suất An trúng giải nhất là 0,0001 và xác suất An trúng giải nhì là 0,0036.

Bài 18 trang 73 SBT Toán 10 tập 2 Kết nối tri thức

Khi tham gia một trò chơi bốc thăm trúng thưởng, mỗi người chơi chọn một bộ 6 số đôi một khác nhau từ 45 số: 1, 2, ..., 45, chẳng hạn bạn Bình chọn bộ số {4, 12, 20, 31, 32, 33}. Sau đó, người quản trò bốc thăm ngẫu nhiên 6 quả bóng (không hoàn lại) từ một thùng kín đựng 45 quả bóng như nhau ghi các số 1, 2, ..., 45. Bộ 6 số ghi trên 6 quả bóng đó, gọi là bộ số trúng thưởng. Nếu bộ số của người chơi trùng với 4 số của bộ số trúng thưởng thì người chơi trúng giải nhì. Tính xác suất bạn Bình trúng giải nhì khi chơi.

Lời giải:

Không gian mẫu Ω là tập hợp tất cả các tập con có 6 phần tử của tập {1,2,..., 44, 45}

\(n(\Omega ) = C_{45}^6 = 8145000\)

Gọi E là biến cố: “Bạn Bình trúng giải nhi”.

 E là tập hợp tất cả các tập con gồm sáu phần tử của tập {1; 2; 3; ...; 45} có tính chất:

- Bốn phần tử của nó thuộc tập {4; 12, 20, 31, 32, 33}

- Hai phần tử còn lại không thuộc tập {4; 12; 20, 31, 32, 33}.

Chọn 4 phần tử trong tập {4; 12, 20, 31, 32, 33}. Có \(C_6^4 = 15\) cách

Chọn 2 phần tử còn lại trong 39 phần tử của tập {1; 2; ..., 44, 45} \{4; 12, 20, 31, 32, 33} có  \(C_{39}^2 = 741\) cách.

 Tập E có 15 . 741=11 115 phần tử.

Vậy xác suất bạn Bình trúng giải nhì khi chơi là: \(P(E) = \frac{{11115}}{{8145000}} = 0,00136\)

Sachbaitap.com