Giải SGK Toán 11 Cánh Diều tập 2 trang 115

Bài 1 trang 115 SGK Toán 11 - Cánh Diều tập 2

Quan sát và cho biết chiếc đèn treo ở Hình 96a, trạm khảo sát trắc địa ở Hình 96b có dạng hình gì.

Phương pháp:

uan sát hình ảnh và trả lời câu hỏi.

Lời giải:

Quan sát Hình 96a và 96b ta thấy:

⦁ Chiếc đèn treo ở Hình 96a là hình lăng trụ lục giác đều vì có các mặt bên là hình chữ nhật và vuông góc với mặt đáy, mặt đáy là lục giác đều.

⦁ Trạm khảo sát trắc địa là hình chóp cụt tứ giác đều vì có hai đáy là hình vuông và nằm trên hai mặt phẳng song song với nhau; mỗi mặt bên đều là hình thang cân; các đường thẳng chứa cạnh bên đều cùng đi qua một điểm.

Bài 2 trang 115 SGK Toán 11 - Cánh Diều tập 2

Cho hình chóp đều \(S.ABCD\) có các cạnh bên và các cạnh đáy đều bằng \(a\).

a) Chứng minh rằng các tam giác \(ASC\) và \(BSD\) là tam giác vuông cân.

b) Gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\), chứng minh rằng đường thẳng \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\).

c) Chứng minh rằng góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^ \circ }\).

Phương pháp:

a) Chứng minh tam giác có 2 cạnh bằng nhau và có một góc vuông.

b) Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

c) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải:

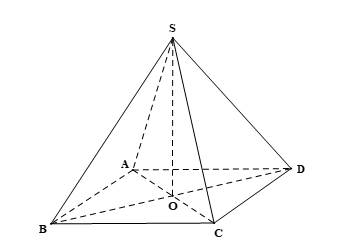
a) Do S.ABCD là hình chóp đều nên SA = SB = SC = SD = a.

Vì ABCD là hình vuông nên AC = BC và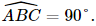 

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

Mà AC = BD nên BD² = AC² = 2a².

⦁ Xét ∆ASC có: SA² + SC² = a² + a² = 2a² = AC².

Nên theo định lí Pythagore đảo ta có tam giác ASC vuông tại S.

Mà SA = SC nên tam giác ASC vuông cân tại S.

⦁ Xét tam giác BSD có: SB² + SD² = a² + a² = 2a² = BD².

Nên theo định lí Pythagore đảo ta có tam giác BSD vuông tại S.

Mà SB = SD nên tam giác BSD vuông cân tại S.

b) Do ABCD là hình vuông và O = AC ∩ BD nên O là trung điểm của AC và BD.

Xét ∆ASC vuông cân tại S có: SO là đường trung tuyến (do O là trung điểm của AC) nên cũng đồng thời là đường cao của tam giác. Do đó SO ⊥ AC.

Xét ∆BSD vuông cân tại S có: SO là đường trung tuyến (do O là trung điểm của BD) nên cũng đồng thời là đường cao của tam giác. Do đó SO ⊥ BD.

Ta có: SO ⊥ AC, SO ⊥ BD và AC ∩ BD = O trong (ABCD).

Do đó SO ⊥ (ABCD).

c) Vì SO ⊥ (ABCD) nên OA là hình chiếu của SA trên (ABCD).

Suy ra góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng góc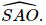 

Lại có tam giác ASC là tam giác vuông cân tại S nên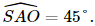 

Vậy góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.

Bài 3 trang 115 SGK Toán 11 - Cánh Diều tập 2

Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^ \circ }\).

a) Chứng minh rằng hai mặt phẳng \(\left( {ACC'A'} \right)\) và \(\left( {BDD'B'} \right)\) vuông góc với nhau.

b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD'\).

Phương pháp:

‒ Cách chứng minh hai mặt phẳng vuông góc: Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng còn lại.

‒ Cách tính khoảng cách giữa hai đường thẳng song song: Tính khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia.

Lời giải:

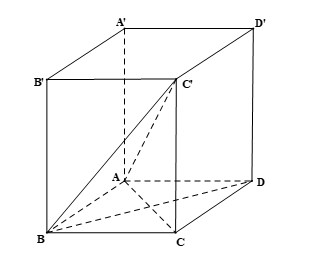
a) Ta có ABCD.A’B’C’D’ là hình lăng trụ đứng nên BB’ ⊥ (ABCD).

Mà AC ⊂ (ABCD) nên BB’ ⊥ AC.

Do ABCD là hình vuông nên AC ⊥ BD.

Ta có: AC ⊥ BB’, AC ⊥ BD và BB’ ∩ BD = B trong (BDD’B’).

Suy ra AC ⊥ (BDD’B’).

Hơn nữa AC ⊂ (ACC’A’).

Từ đó, ta có (ACC’A’) ⊥ (BDD’B’).

b) Vì ABCD.A’B’C’D’ là hình lăng trụ đứng nên C’D’DC là hình chữ nhật.

Do đó CD // C’D’.

Mà CD // AB (do ABCD là hình vuông) nên AB // C’D’.

Khi đó, d(AB, C’D’) = d(B, C’D’). (1)

Vì ABCD.A’B’C’D’ là hình lăng trụ đứng và đáy ABCD là hình vuông nên A’B’C’D’ cũng là hình vuông.

Do đó C’D’ ⊥ B’C’.

Ta có: C’D’ ⊥ B’C’;

           C’D’ ⊥ C’C (do C’D’DC là hình chữ nhật);

           B’C’ ∩ C’C = C’ trong (BCC’B’).

Suy ra C’D’ ⊥ (B’C’CB).

Mà BC’ ⊂ (B’C’CB) nên C’D’ ⊥ BC’.

Khi đó d(B, C’D’) = BC’. (2)

Từ (1) và (2) ta có: d(AB, C’D’) = BC’.

Do ABCD.A’B’C’D’ là hình lăng trụ đứng nên C’C ⊥ (ABCD).

Khi đó AC là hình chiếu của AC’ trên (ABCD).

Suy ra góc giữa đường thẳng AC’ và mặt phẳng (ABCD) bằng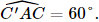 

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

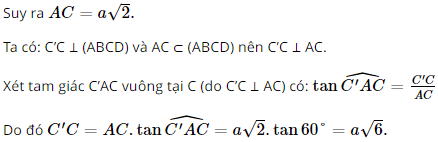
Do ABCD.A’B’C’D’ là hình lăng trụ đứng nên B’C’CB là hình chữ nhật.

Suy ra C’C ⊥ BC.

Áp dụng định lí Pythagore vào tam giác C’CB vuông tại C (vì C’C ⊥ BC) có:

BC’² = CC’² + BC²

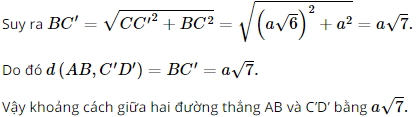
Bài 4 trang 115 SGK Toán 11 - Cánh Diều tập 2

Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó. 

Phương pháp:

Sử dụng công thức tính thể tích khối hộp chữ nhật với ba kích thước \(a,b,c\): \(V = abc\).

Lời giải:

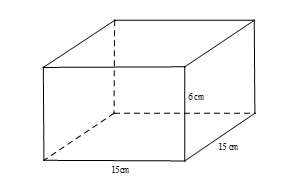
Thể thể tích của chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm là:

V = abc = 15.15.6 = 1 350 (cm³).

Bài 5 trang 115 SGK Toán 11 - Cánh Diều tập 2

Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3 g/cm.

Phương pháp:

‒ Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).

‒ Sử dụng công thức tính khối lượng: \(m = D.V\).

Lời giải:

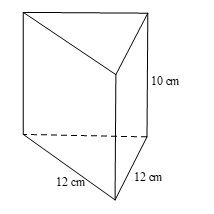
Vì đáy của miếng pho mát là tam giác vuông cân có cạnh góc vuông bằng 12 cm nên ta có diện tích đáy là: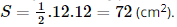 

Thể tích của miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và diện tích đáy 73 cm² là:

V = Sh = 72.10 = 720 (cm³).

Khối lượng của miếng pho mát với khối lượng riêng 3 g/cm³ và thể tích 720 cm³ là:

m = 3.720 = 2 160 (g).

Bài 6 trang 115 SGK Toán 11 - Cánh Diều tập 2

Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97). Tính theo \(a\) thể tích của đèn đá muối đó, giả sử các cạnh đáy và các cạnh bên đều bằng \(a\).

Phương pháp:

Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải:

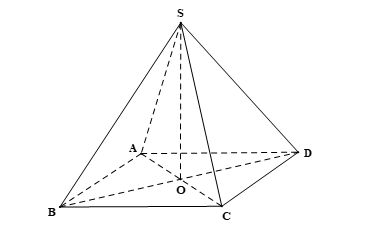
Mô hình hóa đèn đá muối bằng hình chóp tứ giác đều S.ABCD cạnh a.

Vì S.ABCD là hình chóp tứ giác đều nên đáy ABCD là hình vuông nên gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC, BD và AC = BD.

Suy ra OA = OB = OC = OD.

Như vậy, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

Do đó, O là chân đường cao của hình chóp S.ABCD hay SO ⊥ (ABCD).

Mà AC ⊂ (ABCD) nên SO ⊥ AC.

Do ABCD là hình vuông nên 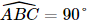 do đó tam giác ABC vuông tại B.

Áp dụng định lí Pythagore trong tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

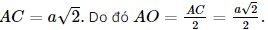
Áp dụng định lí Pythagore trong tam giác SAO vuông tại O (do SO ⊥ AC) có:

SA² = AO² + SO²

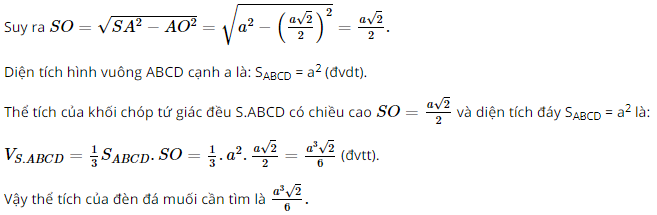
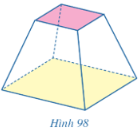
Bài 7 trang 115 SGK Toán 11 - Cánh Diều tập 2

Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều (Hình 98). Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m . Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị đồng.

Phương pháp:

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'}  + S'} \right)\).

Lời giải:

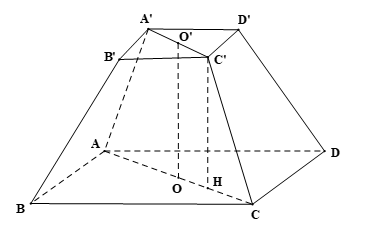
Mô hình hóa chân tháp của bài toán bằng khối chóp cụt tứ giác đều ABCD.A’B’C’D’, với O, O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.

Như vậy ta có:

⦁ ABCD là hình vuông cạnh 5 có diện tích S_ABCD = 5² = 25;

⦁ A’B’C’D’ là hình vuông cạnh 2 có diện tích S_{A’B’C’D’} = 2² = 4;

⦁ Các cạnh bên A’A, B’B, C’C, D’D có độ dài bằng 3;

⦁ OO’ vuông góc với (ABCD) và (A’B’C’D’).

Do ABCD là hình vuông nên 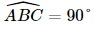 do đó tam giác A’B’C’ vuông tại B’.

Áp dụng định lí Pythagore trong tam giác A’B’C’ vuông tại B’ có:

A’C’² = A’B’² + B’C’² = 2² + 2² = 8.

Dễ thấy: (ABCD) ∩ (A’C’CA) = AC;

              (A’B’C’D’) ∩ (A’C’CA) = A’C’.

Mà (ABCD) // (A’B’C’D’).

Suy ra AC // A’C’ hay A’C’CA là hình thang.

Xét hình thang A’C’CA, kẻ C’H ⊥ AC (H ∈ AC).

Vì OO’ ⊥ (ABCD) và AC ⊂ (ABCD) nên OO’ ⊥ AC.

Do đó C’H // OO’ (cùng vuông góc với AC).

Mà O’C’ // OH (do A’C’ // AC)

Suy ra O’C’HO là hình bình hành.

Vậy số tiền để mua bê tông tươi làm chân tháp khoảng 40 538 432 đồng.

Sachbaitap.com