Giải SGK Toán 11 Cánh Diều tập 2 trang 56, 57, 58
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 trang 56, 57, 58 SGK Toán lớp 11 Cánh Diều tập 2. Trong một trận động đất, năng lượng giải tỏa E (đơn vị: Jun, kí hiệu J) tại tâm địa chấn ở M độ Richter được xác định xấp xỉ bởi công thức:
Xem thêm: Bài tập cuối chương 6
Bài 1 trang 56 SGK Toán 11 - Cánh Diều tập 2
Điều kiện xác định của \({x^{ - 3}}\) là
A. \(x \in \mathbb{R}\)
B. \(x \ge 0\)
C. \(x \ne 0\)
D. \(x > 0\)
Phương pháp:
Dựa vào tập xác định của các hàm đã học để xác định .
Lời giải:
Đáp án đúng là: C
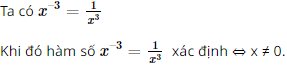
Bài 2 trang 56 SGK Toán 11 - Cánh Diều tập 2
Điều kiện xác định của \({x^{\frac{3}{5}}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ge 0\)
C. \(x \ne 0\)
D. \(x > 0\)
Phương pháp:
Dựa vào tập xác định của các hàm đã học để xác định.
Lời giải:
Đáp án đúng là: A
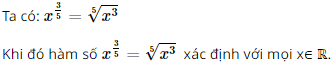
Bài 3 trang 56 SGK Toán 11 - Cánh Diều tập 2
Tập xác định của hàm số \(y = {\log _{0,5}}\left( 2x -x^2 \right)\) là:
A. \(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
B. \(\mathbb{R}\backslash \{0; 2\} \)
C. \([0; 2]\)
D. \((0;2)\)
Phương pháp:
Dựa vào tập xác định của các hàm đã học để xác định .
Lời giải:
Đáp án đúng là: D
Hàm số y = log0,5(2x – x2) xác định ⇔ 2x – x2 > 0
⇔ x2 – 2x < 0 ⇔ x(x – 2) < 0
⇔ 0 < x < 2.
Vậy tập xác định của y = log0,5(2x – x2) là (0; 2).
Bài 4 trang 56 SGK Toán 11 - Cánh Diều tập 2
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. \(y = {(0,5)^x}\)
B. \(y = {\left( {\frac{2}{3}} \right)^x}\)
C. \(y = {(\sqrt 2 )^x}\)
D. \(y = {\left( {\frac{e}{\pi }} \right)^x}\)
Phương pháp:
Dựa vào tính đồng biến, nghịch biến của hàm số mũ để xét.
Lời giải:
Đáp án đúng là: C
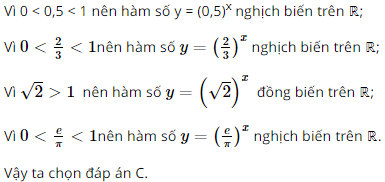
Bài 5 trang 56 SGK Toán 11 - Cánh Diều tập 2
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
A. \(y = {\log _3}x\)
B. \(y = {\log _{\sqrt 3 }}x\)
C. \({\log _{\frac{1}{e}}}x\)
D. \(y = {\log _\pi }x\)
Phương pháp:
Dựa vào tính đồng biến, nghịch biến của hàm số lôgarit để xét.
Lời giải:
Đáp án đúng là: C

Bài 6 trang 56 SGK Toán 11 - Cánh Diều tập 2
Nếu \({3^x} = 5\) thì \({3^{2x}}\) bằng:
A. 15
B. 125
C. 10
D. 25
Phương pháp:
Dựa vào các công thức biến đổi lũy thừa để tính
Lời giải:
Đáp án đúng là: D
Ta có: 32x = (3x)2 = 52 = 25.
Bài 7 trang 56 SGK Toán 11 - Cánh Diều tập 2
Cho \(A = {4^{{{\log }_2}3}}\). Khi đó giá trị của A bằng
A. 9
B. 6
C. \(\sqrt 3 \)
D. 81
Phương pháp:
Dựa vào công thức biến đổi của lôgarit để tính.
Lời giải:
Đáp án đúng là: A
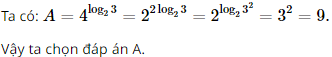
Bài 8 trang 56 SGK Toán 11 - Cánh Diều tập 2
Cho \({\log _a}b = 3\) thì \({\log _a}{b^2}\) bằng:
A. 9
B. 5
C. 6
D. 8
Phương pháp:
Dựa vào công thức biến đổi của lôgarit để tính.
Lời giải:
Đáp án đúng là: C
Ta có: logab2 = 2logab = 2 . 3 = 6.
Bài 9 trang 56 SGK Toán 11 - Cánh Diều tập 2
Nghiệm của phương trình \({3^{2x - 5}} = 27\) là
A. 1
B. 4
C. 6
D. 7
Phương pháp:
Dựa vào cách giải phương trình mũ đã học để tính
Lời giải:
Đáp án đúng là: B
Ta có: 32x – 5 = 27 ⇔32x – 5 = 33 ⇔ 2x – 5 = 3 ⇔ x = 4.
Bài 10 trang 56 SGK Toán 11 - Cánh Diều tập 2
Nghiệm của phương trình \({\log _{0,5}}(2 - x) = - 1\)
A. 0
B. 2,5
C. 1,5
D. 2
Phương pháp:
Dựa vào cách giải phương trình lôgarit đã học để tính.
Lời giải:
Đáp án đúng là: A
Ta có log0,5(2 – x) = –1 ⇔ 2 – x = 0,5–1 ⇔ 2 – x = 2 ⇔ x = 0.
Bài 11 trang 56 SGK Toán 11 - Cánh Diều tập 2
Tập nghiệm của bất phương trình \({(0,2)^x} > 1\) là:
A. \(\left( { - \infty ;0,2} \right)\)
B. \(\left( {0,2; + \infty } \right)\)
C. \(\left( {0; + \infty } \right)\)
D. \(\left( { - \infty ;0} \right)\)
Phương pháp:
Dựa vào cách giải bất phương trình mũ để tính.
Lời giải:
Đáp án đúng là: D
Ta có (0,2)x > 1 ⇔ x < log0,21 ⇔ x < 0.
Vậy bất phương trình đã cho có tập nghiệm là (–∞; 0).
Bài 12 trang 57 SGK Toán 11 - Cánh Diều tập 2
Tập nghiệm của bất phương trình \({\log _{\frac{1}{4}}}x > - 2\) là:
A. \(\left( { - \infty ;16} \right)\)
B. \(\left( {16; + \infty } \right)\)
C. \((0;16)\)
D. \(\left( { - \infty ;0} \right)\)
Phương pháp:
Dựa vào cách giải bất phương trình mũ để tìm tập nghiệm.
Lời giải:
Đáp án đúng là: C
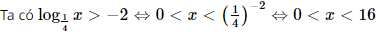
Vậy bất phương trình đã cho có tập nghiệm là (0; 16).
Bài 13 trang 57 SGK Toán 11 - Cánh Diều tập 2
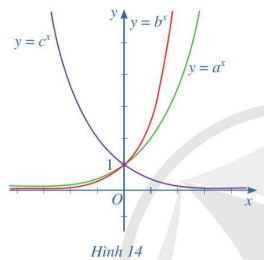
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Phương pháp:
Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số mũ để suy ra.
Lời giải:
Đáp án đúng là: A
Từ các đồ thị hàm số trên Hình 14 ta thấy:
⦁ Hàm số y = cx nghịch biến trên ℝ nên 0 < c < 1;
⦁ Hai hàm số y = ax và y = bx đồng biến trên ℝ nên a > 1 và b > 1.
![]()
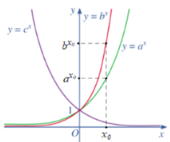
Thay cùng giá trị của x = x0 (với x0 > 0) vào hai hàm số y = ax và y = bx ta thấy nên a < b
Suy ra c < a < b.
Bài 14 trang 57 SGK Toán 11 - Cánh Diều tập 2
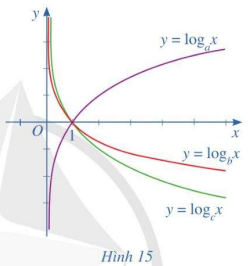
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?

A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Phương pháp:
Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số lôgarit để suy ra.
Lời giải:
Đáp án đúng là: D
Từ các đồ thị hàm số trên Hình 15 ta thấy:
⦁ Hàm số y = logax đồng biến trên (0; +∞) nên a > 1;
⦁ Hai hàm số y = logbx và y = logcx nghịch biến trên (0; +∞) nên 0 < b < 1; 0 < c < 1.
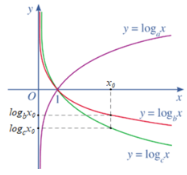
Thay cùng giá trị của x = x0 (với x0 ∈ (0; +∞)) vào hai hàm số ta thấy logbx0 > logcx0
Mà 0 < b < 1; 0 < c < 1 nên b < c.
Suy ra b < c < a.
Bài 15 trang 57 SGK Toán 11 - Cánh Diều tập 2
a) \(A = \sqrt[3]{{5\sqrt {\frac{1}{5}} }};\,\,a = 5\)
b) \(B = \frac{{4\sqrt[5]{2}}}{{\sqrt[3]{4}}};\,\,a = \sqrt 2 \)
Phương pháp:
Dựa vào tính chất lũy thừa để tính.
Lời giải:
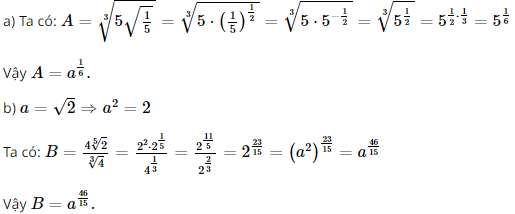
Bài 16 trang 57 SGK Toán 11 - Cánh Diều tập 2
Cho x; y là các số thực dương. Rút gọn mỗi biểu thức sau:
\(A = \frac{{{x^{\frac{5}{4}}}y + x.{y^{\frac{5}{4}}}}}{{\sqrt[4]{x} + \sqrt[4]{y}}}\)
\(B = {\left( {\sqrt[7]{{\frac{x}{y}\sqrt[5]{{\frac{y}{x}}}}}} \right)^{\frac{{35}}{4}}}\)
Phương pháp:
Dựa vào tính chất lũy thừa để tính.
Lời giải:
Ta có:
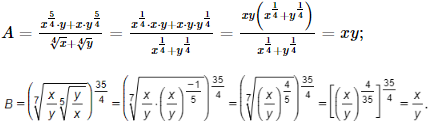
Bài 17 trang 57 SGK Toán 11 - Cánh Diều tập 2
Tìm tập xác định của mỗi hàm số sau:
a) \(y = \frac{5}{{{2^x} - 3}}\)
b) \(y = \sqrt {25 - {5^x}} \)
c) \(y = \frac{x}{{1 - \ln x}}\)
d) \(y = \sqrt {1 - {{\log }_3}x} \)
Phương pháp:
Dựa vào tập xác định của hàm số đã học để xác định tập hàm định của từng hàm.
Lời giải:

Bài 18 trang 58 SGK Toán 11 - Cánh Diều tập 2
Cho \(a > 0;a \ne 1;{a^{\frac{3}{5}}} = b\)
a) Viết \({a^6};{a^3}b;\frac{{{a^9}}}{{{b^9}}}\) theo lũy thừa cơ số b
b) Tính \({\log _a}b;\,{\log _a}\left( {{a^2}{b^5}} \right);\,{\log _{\sqrt[5]{a}}}\left( {\frac{a}{b}} \right)\)
Phương pháp:
Dựa vào tính chất lũy thừa để biến đổi.
Lời giải:
Ta có:
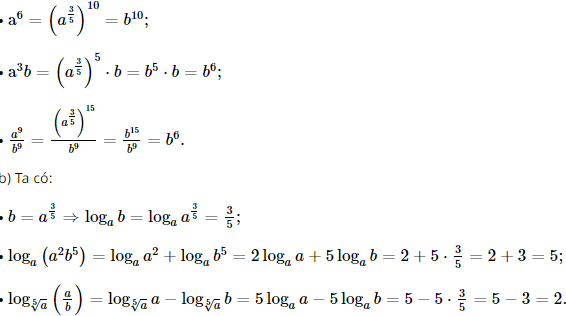
Bài 19 trang 58 SGK Toán 11 - Cánh Diều tập 2
Giải mỗi phương trình sau:
a) \({3^{{x^2} - 4x + 5}} = 9\)
b) \(0,{5^{2x - 4}} = 4\)
c) \({\log _3}(2x - 1) = 3\)
d) \(\log x + \log (x - 3) = 1\)
Phương pháp:
Dựa vào kiến thức giải phương trình logarit và phương trình mũ để làm bài
Lời giải
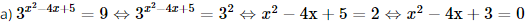
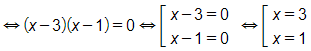
Vậy phương trình có nghiệm là x ∈ {1; 3}.
b) 0,52x–4 = 4 ⇔ 2x – 4 = log0,54
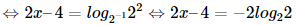
⇔ 2x – 4 = –2 ⇔ 2x = 2 ⇔ x = 1.
Vậy phương trình có nghiệm là x = 1.
c) log3(2x – 1) = 3
⇔ 2x – 1 = 33 ⇔ 2x – 1 = 27
⇔ 2x = 28 ⇔ x = 14.
Vậy phương trình có nghiệm là x = 14.
d) logx + log(x – 3) = 1
Điều kiện xác định là 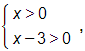 tức là x > 3. Ta có:
tức là x > 3. Ta có:
logx + log(x – 3) = 1
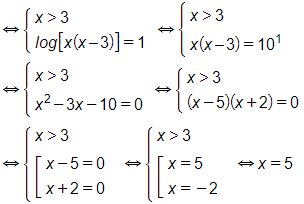
Vậy phương trình có nghiệm là x = 5.
Bài 20 trang 58 SGK Toán 11 - Cánh Diều tập 2
Giải mỗi bất phương trình sau:
a) \({5^x} < 0,125\)
b) \({\left( {\frac{1}{3}} \right)^{2x + 1}} \ge 3\)
c) \({\log _{0,3}}x > 0\)
d) \(\ln (x + 4) > \ln (2x - 3)\)
Phương pháp:
Dựa vào kiến thức giải bất phương trình logarit và phương trình mũ để làm bài
Lời giải:
a) 5x < 0,125⇔ x < log50,125
Vậy bất phương trình có tập nghiệm là (−∞; log50,125).
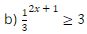
⇔ 2x + 1 ≤ –1
⇔ 2x ≤ –2
⇔ x ≤ –1
Vậy bất phương trình có tập nghiệm là (–∞; –1].
c) log0,3x > 0⇔0 < x < 0,30 ⇔0 < x < 1
Vậy bất phương trình có tập nghiệm là (0; 1).
d) ln(x + 4) > ln(2x – 3)
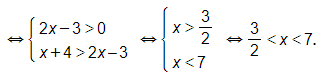
Vậy bất phương trình có tập nghiệm là 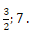
Bài 21 trang 58 SGK Toán 11 - Cánh Diều tập 2
Trong một trận động đất, năng lượng giải tỏa E (đơn vị: Jun, kí hiệu J) tại tâm địa chấn ở M độ Richter được xác định xấp xỉ bởi công thức: \(\log E \approx 11,4 + 1,5M\)
a) Tính xấp xỉ năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter.
b) Năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng bao nhiêu lần năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter?
Phương pháp:
Dựa vào công thức đề bài cho áp dụng thêm cách giải phương trình
Lời giải:
a) Thay M = 5 vào công thứclogE ≈ 11,4 + 1,5M, ta cónăng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter là:
logE ≈ 11,4 + 1,5 . 5 =18,9
Suy ra E ≈ 1018,9 (J)
Vậy năng lượng giải toả tại tâm địa chấn ở 5 độ Richter là E ≈ 1018,9 J.
b) Thay M = 8 vào công thứclogE ≈ 11,4 + 1,5M, ta có năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter là:
logE ≈ 11,4 + 1,5 . 8 =23,4
Suy ra E ≈ 1023,4 (J)
Do đó năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng 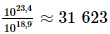 lần năng lượng giải tỏa tại tâmđịa chấn ở 5 độ Richter.
lần năng lượng giải tỏa tại tâmđịa chấn ở 5 độ Richter.
Bài 22 trang 58 SGK Toán 11 - Cánh Diều tập 2
Trong cây cối có chất phóng xạ \({}_6^{14}C\). Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ của nó bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại. Xác định độ tuổi của mẫu gỗ cổ đó. Biết chu kì bán rã của \({}_6^{14}C\)là \(T = 5730\) năm, độ phóng xạ của chất phóng xạ tại thời điểm t được cho bởi công thức \(H = {H_0}{e^{ - \lambda t}}\) với \({H_0}\) là độ phóng xạ ban đầu (tại thời điểm t = 0); \(\lambda = \frac{{\ln 2}}{T}\) là hằng số phóng xạ.
Phương pháp:
Dựa vào công thức đã cho để tính.
Lời giải:
Do độ phóng xạ của 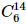 bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại nên ta có:
bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại nên ta có:
H = 86%H0
⇔ H0e–λt = 0,86H0
⇔ e–λt = 0,86
⇔ –λt = ln0,86
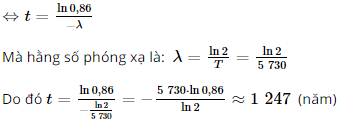
Vậy độ tuổi của mẫu gỗ cổ đó là khoảng 1 247 năm.
Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 8
- Bài 6. Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
- Bài 5. Khoảng cách
- Bài 4. Hai mặt phẳng vuông góc
- Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- CHƯƠNG VIII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN, PHÉP CHIẾU VUÔNG GÓC
- Bài tập cuối chương 7
- Bài 3. Đạo hàm cấp hai
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!