Giải SGK Toán 11 Cánh Diều tập 2 trang 76

Bài 1 trang 76 SGK Toán 11 - Cánh Diều tập 2

Cho \(u = u(x),v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

A. \((uv)' = u'v'\)

B. \((uv)' = uv'\)

C. \((uv)' = u'v\)

D. \((uv)' = u'v + uv'\)

Phương pháp:

Dựa vào công thức tính đạo hàm của phép nhân để rút ra đáp án.

Lời giải:

Đáp án đúng là: D

Ta có: (uv)' = u'v + uv'.

Bài 2 trang 76 SGK Toán 11 - Cánh Diều tập 2

Cho \(u = u(x),v = v(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

A. \(\left( {\frac{u}{v}} \right)' = \frac{{u'}}{{v'}}\) với \(v = v(x) \ne 0,v = v'(x) \ne 0\)

B. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{v}\) với \(v = v(x) \ne 0\)

C. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) với \(v = v(x) \ne 0\)

D. \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{v'}}\) với \(v = v(x) \ne 0;\,\,v' = v'(x) \ne 0\)

Phương pháp:

Dựa vào công thức tính đạo hàm của phép chia để rút ra đáp án.

Lời giải:

Đáp án đúng là: C

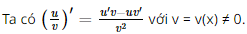
Bài 3 trang 76 SGK Toán 11 - Cánh Diều tập 2

Tính đạo hàm của mỗi hàm số sau:

a)     \(y = \left( {{x^2} + 2x} \right)\left( {{x^3} - 3x} \right)\)

b)    \(y = \frac{1}{{ - 2x + 5}}\)

c)     \(y = \sqrt {4x + 5} \)

d)    \(y = \sin x\cos x\)

e)     \(y = x{e^x}\)

f)      \(y = {\ln ^2}x\)

Phương pháp:

Dựa vào công thức đạo hàm của các hàm để tính.

Lời giải:

 a) Xét hàm số y = (x² + 2x)(x³ – 3x), ta có:

y' = (x² + 2x)'(x³ – 3x) + (x² + 2x)(x³ – 3x)'

= (2x + 2)(x³ – 3x) + (x² + 2x)(3x² – 3)

= 2x⁴ – 6x² + 2x³ – 6x + 3x⁴ – 3x² + 6x³ – 6x

= 5x⁴ + 8x³ – 9x² – 12x.

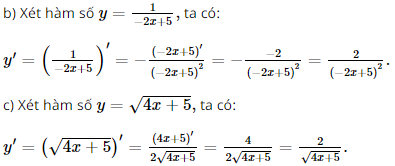
d) Xét hàm số y = sinxcosx

Cách 1.

y' = (sinxcosx)' = (sinx)'.cosx + sinx.(cosx)'

= cosx.cosx + sinx.(–sinx)

= cos²x – sin²x = cos2x.

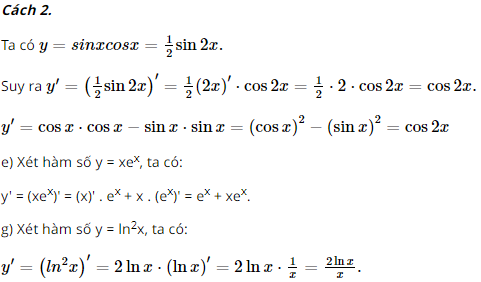
Bài 4 trang 76 SGK Toán 11 - Cánh Diều tập 2

Tính đạo hàm cấp hai của mỗi hàm số sau:

a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\)

b)\(y = \frac{2}{{3 - x}}\)

c) \(y = \sin 2x\cos x\)

d) \(y = {e^{ - 2x + 3}}\)

e) \(y = \ln (x + 1)\)

f) \(y = \ln ({e^x} + 1)\)

Phương pháp:

Dựa vào định nghĩa đạo hàm cấp hai để tính.

Lời giải:

a) Xét hàm số y = 2x⁴ – 3x³ + 5x², ta có:

y' = 8x³ – 9x² + 10x;

y'' = 24x² – 18x + 10.

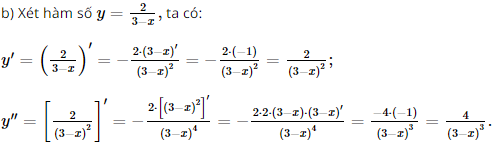
c) Xét hàm số y = sin2xcosx, ta có:

y' = (sin2xcosx)' = (sin2x)'.cosx + sin2x.(cosx)'

    = 2cos2x.cosx – sin2x.sinx

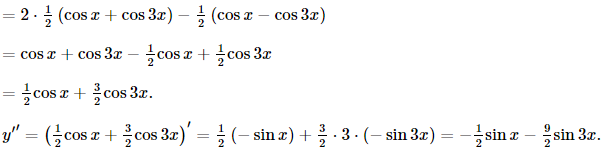
d) Xét hàm số y = e^{–2x + 3}, ta có:

y' = (e^{–2x + 3})' = (–2x + 3)' . e^{–2x + 3} = –2e^–2x+3;

y'' = (–2e^–2x+3)' = –2.(–2x + 3)'.e^–2x+3 = 4e^–2x+3.

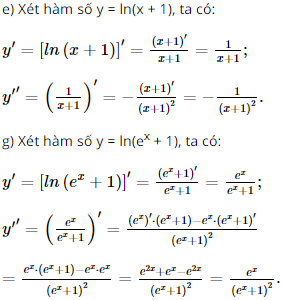
Bài 5 trang 76 SGK Toán 11 - Cánh Diều tập 2

Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức \(v(t) = 2t + {t^2}\), trong đó t > 0, t tính bằng giây và v(t) tính bằng m/s. Tìm gia tức thời của chất điểm:

a) Tại thời điểm t = 3(s)

b) Tại thời điểm mà vận tốc của chất điểm bằng 8 m/s

Phương pháp:

Dựa vào hàm số đạo hàm để tìm từng đại lượng sau đó thay số.

Lời giải:

Vận tốc của chất điểm chuyển động được biểu thị bởi công thức v(t) = t² + 2t.

a) Gia tốc tức thời của chất điểm: a(t) = v'(t) = 2t + 2.

Gia tốc tức thời của chất điểm tại t = 3 (s) là:

a(3) = 2 . 3 + 2 = 8 (m/s²).

b) Để vận tốc của chất điểm bằng 8 m/s thì: t² + 2t = 8

Suy ra t² + 2t – 8 = 0

Do đó t = 2 (thỏa mãn) hoặc t = –4 (không thỏa mãn)

Tại t = 2 thì a(2) = 2 . 2 + 2 = 6 (m/s²).

Vậy tại thời điểm vận tốc của chất điểm bằng 8 m/s thì gia tốc tức thời là 6 m/s².

Bài 6 trang 76 SGK Toán 11 - Cánh Diều tập 2

Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động \(x = 4\cos \left( {\pi t - \frac{{2\pi }}{3}} \right) + 3\), trong đó t tính bằng giây và x tính bằng centimet

a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s)

b) Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0.

Phương pháp:

Dựa vào hàm số đạo hàm để tìm từng đại lượng sau đó thay số.

Lời giải:

Sachbaitap.com