Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 trang 105, 106 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp CMND bằng
Xem thêm: BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
Bài 1 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Khẳng định nào sau đây là sai?
A. \(\cos (\alpha + \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \).
B. \(\sin \left( {\frac{\pi }{2} + \alpha } \right) = \cos \alpha \)
C. \(\sin (\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \).
D. \(\cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \).
Phương pháp:
Nhớ lại công thức lượng giác
Lời giải:
Đáp án đúng là: A
Ta có: 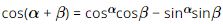 nên đáp án A sai.
nên đáp án A sai.
Bài 2 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Khẳng định nào sau đây là đúng?
A. Hàm số \(y = \sin x\) tuần hoàn với chu kì \(\pi \).
B. Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi \).
C. Hàm số \(y = \tan x\) tuần hoàn với chu kì \(2\pi \).
D. Hàm số \(y = \cot x\) tuần hoàn với chu kì \(2\pi \).
Phương pháp:
Hàm số \(y = \sin x\), \(y = \cos x\) tuần hoàn với chu kì \(2\pi \). Hàm số \(y = \tan x\), \(y = \cot x\) tuần hoàn với chu kì \(\pi \).
Lời giải:
Đáp án đúng là: B
Hàm số y = sinx; y = cosx tuần hoàn với chu kì 2π.
Hàm số y = tanx; y = cotx tuần hoàn với chu kì π.
Bài 3 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {5^n}\). Số hạng \({u_{2n}}\) bằng
A. \({2.5^n}\).
B. \({25^n}\).
C. \({10^n}\)
D. \({5^{{n^2}}}\).
Phương pháp:
Tính số hạng của một dãy số
Lời giải:
Đáp án đúng là: B
Ta có u2n = 52n = (52)n = 25n.
Bài 4 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Dãy số \(\left( {{u_n}} \right)\) cho bởi công thức số hạng tổng quát nào dưới đây là dãy số tăng?
A. \(\frac{1}{{{n^2} + 1}}\).
B. \({2^{ - n}}\).
C. \({\log _{\frac{1}{2}}}n\).
D. \(\frac{n}{{n + 1}}\).
Phương pháp:
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có \({u_{n + 1}} > {u_n}\) với mọi \(n \in {\mathbb{N}^*}\)
Lời giải:
Đáp án đúng là: D
+)![]()
Xét un + 1 – un =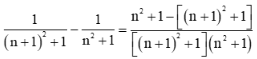
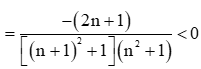 , với mọi n ∈">∈ ℕ*
, với mọi n ∈">∈ ℕ*
Do đó 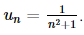 là dãy số giảm.
là dãy số giảm.
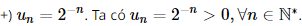
Xét 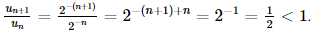
Do đó 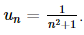 là dãy số giảm.
là dãy số giảm.
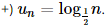
Có a = 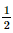 nên
nên 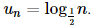 luôn nghịch biến với n ∈">∈ ℕ*.
luôn nghịch biến với n ∈">∈ ℕ*.
Do đó 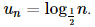 là dãy số giảm.
là dãy số giảm.
+)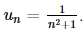
Xét un + 1 – un =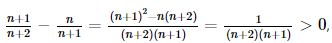 với mọi n ∈">∈ ℕ*.
với mọi n ∈">∈ ℕ*.
Do đó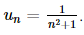 là dãy số tăng.
là dãy số tăng.
Bài 5 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Khẳng định nào sau đây là sai?
A. Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \ge 0\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
B. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{x} = - \infty \).
C. Nếu \(|q| \le 1\) thì \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\).
D. \(\mathop {\lim }\limits_{n \to + \infty } \frac{{\sin n}}{{n + 1}} = 0\).
Phương pháp:
Quy tắc tìm giới hạn
Lời giải:
Đáp án đúng là: C
+) Theo quy tắc tìm giới hạn thì: Nếu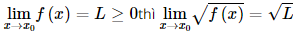 nên A đúng.
nên A đúng.
+)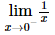 limx→0−1x=−∞">=−∞nên B đúng.
limx→0−1x=−∞">=−∞nên B đúng.
+) Nếu |q| < 1 thì  , nếu |q| = 1 thì q = 1 hoặc q = – 1, do đó qn = 1 hoặc qn = – 1.
, nếu |q| = 1 thì q = 1 hoặc q = – 1, do đó qn = 1 hoặc qn = – 1.
Vậy C sai.
+) Ta có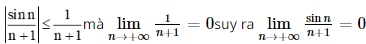 nên D đúng.
nên D đúng.
Bài 6 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Hàm số nào dưới đây không liên tục trên \(\mathbb{R}\)?
A. \(y = \tan x\).
B. \(y = \frac{{2{x^2} + 3x - 1}}{{{x^2} + 1}}\).
C. \(y = \sin x\).
D. \(y = |x|\).
Phương pháp:
Hàm số sơ cấp liên tục trên tập xác định của chúng.
Lời giải:
Đáp án đúng là: A
Các hàm số y= 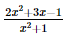 ,; y = sinx; y = |x| đều liên tục trên ℝ.
,; y = sinx; y = |x| đều liên tục trên ℝ.
Hàm số y = tanx có tập xác định là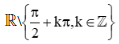 nên hàm số y = tanx không liên tục trên ℝ.
nên hàm số y = tanx không liên tục trên ℝ.
Bài 7 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho \(0 < a \ne 1\). Giá trị của biểu thức \({\log _a}\left( {{a^3} \cdot \sqrt[4]{a}} \right) + {(\sqrt[3]{a})^{{{\log }_a}8}}\) bằng
A. \(\frac{{19}}{4}\).
B. 9 .
C. \(\frac{{21}}{4}\).
D. \(\frac{{47}}{{12}}\).
Phương pháp:
Sử dụng các công thức lôgarit
Lời giải:
Đáp án đúng là: C
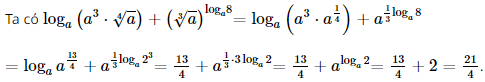
Bài 8 trang 105 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho đồ thị ba hàm số mũ \(y = {a^x},y = {b^x}\) và \(y = {c^x}\) như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
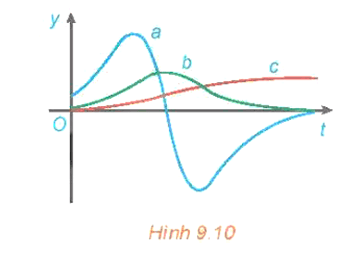
A. \(a > c > b\).
B. \(b > a > c\).
C. \(c > a > b\).
D. \(c > b > a\).
Phương pháp:
Đồ thị hàm số \(y = {a^x}\) đồng biến nếu \(a > 1\)
Đồ thị hàm số \(y = {a^x}\) nghịch biến nếu \(0 < a < 1\)
Lời giải:
Đáp án đúng là: C
Hàm số y = bx có đồ thị đi xuống từ trái sang phải nên hàm số này nghịch biến, từ đó suy ra 0 < b < 1.
Hàm số y = ax và y = cx đồng biến (do đồ thị của các hàm số này đều đi lên từ trái sang phải) nên a, c > 1.
Với x > 0 thì cx > ax nên c > a. Vậy c > a > b.
Bài 9 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Nếu \(f(x) = {\sin ^2}x + x{e^{2x}}\) thì \(f''(0)\) bằng
A. 4.
B. 5 .
C. 6 .
D. 0 .
Phương pháp:
Sử dụng quy tắc kết hợp công thức để tính đạo hàm
Lời giải:
Đáp án đúng là: C
Ta có f'(x) = 2sinxcosx + e2x + 2xe2x = sin2x + e2x + 2xe2x;
f"(x) = 2cos2x + 2e2x + 2e2x + 4xe2x = 2cos2x + 4e2x + 4xe2x .
Ta có f"(0) = 2cos0 + 4 = 2 + 4 = 6.
Bài 10 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Phương trình tiếp tuyến của đồ thị hàm số \(y = - 2{x^3} + 6{x^2} - 5\) tại điểm \(M(3; - 5)\) thuộc đồ thị là
A. \(y = 18x + 49\).
B. \(y = 18x - 49\)
C. \(y = - 18x - 49\).
D. \(y = - 18x + 49\).
Phương pháp:
Nếu hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \({x_0}\) thì phương trình tiếp tuyến của đồ thị hàm số tại điểm \(P\left( {{x_0};{y_0}} \right)\) là \(y - {y_0} = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right),\) trong đó \({y_0} = f\left( {{x_0}} \right)\)
Lời giải:
Đáp án đúng là: D
Ta có y' = −6x2 + 12x, y'(3) = −18.
Phương trình tiếp tuyến của đồ thị hàm số y = −2x3 + 6x2 – 5 tại điểm M(3; −5) là
y = −18(x – 3) – 5 hay y = −18x + 49.
Bài 11 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và \(SA \bot (ABC),SA = a\sqrt 2 \). Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
A. \(\frac{{6a}}{{11}}\).
B. \(\frac{{a\sqrt {66} }}{{11}}\).
C. \(\frac{{a\sqrt 6 }}{{11}}\).
D. \(\frac{{a\sqrt {11} }}{{11}}\).
Phương pháp:
Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P)
Lời giải:
Đáp án đúng là: B
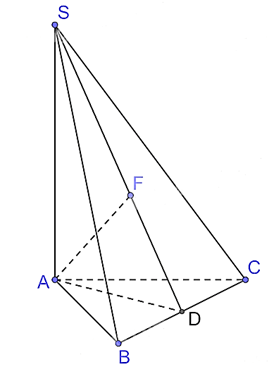
Kẻ AD ⊥ BC tại D.
Vì SA ⊥ (ABC) nên SA ⊥ BC mà AD ^ BC nên BC ⊥ (SAD), suy ra (SBC) ⊥ (SAD).
Kẻ AF ⊥ SD tại F.
Vì (SBC) ⊥ (SAD), (SBC) ∩ (SAD) = SD, AF ⊥ SD nên AF ⊥ (SBC).
Suy ra d(A, (SBC)) = AF.
Vì tam giác ABC đều cạnh a, AD là đường cao nên AD =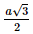
Vì SA ⊥ (ABC) nên SA ⊥ AD hay tam giác SAD vuông tại A.
Xét tam giác SAD vuông tại A, AF là đường cao nên ta có:
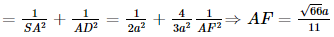
Vậy d(A, (SBC)) =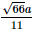
Bài 12 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy ABCD là hình chữ nhật. Biết \(AC = AA' = 2a\). Giá trị lớn nhất của thể tích hình hộp \(ABCD.A'B'C'D'\) bằng
A. \(8{a^3}\).
B. \(6{a^3}\).
C. \(4{a^3}\).
D. \({a^3}\).
Phương pháp:
Thể tích khối lăng trụ \(V = h.S\)
Lời giải:
Đáp án đúng là: C
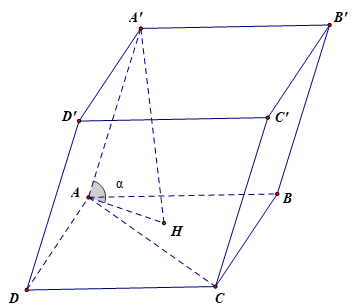
Xét tam giác ABC vuông tại B, có AC2 = AB2 + BC2.
Ta có SABCD = AB . BC ≤ 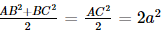 . Dấu “=” xảy ra khi AB = BC.
. Dấu “=” xảy ra khi AB = BC.
Gọi H là hình chiếu của A' trên mặt phẳng (ABCD). Khi đó A'H ⊥ (ABCD). Khi đó AH là hình chiếu của AA' trên mặt phẳng (ABCD).
Gọi α là góc tạo bởi đường thẳng AA' và mặt phẳng (ABCD). Khi đó α=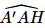
Xét tam giác A'AH vuông tại H có A'H = AA'. sinα">α ≤ AA' = 2a.
Dấu bằng xảy ra khi α">α= 90° hay AA' ⊥⊥ (ABCD).
Do đó VABCD.A'B'C'D' = SABCD . A'H ≤ 2a2 . 2a = 4a3.
Vậy giá trị lớn nhất của thể tích hình hộp ABCD.A'B'C'D' bằng 4a3.
Bài 13 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho tứ diện đều ABCD có cạnh bằng \(a\). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp \(B\).CMND bằng
A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 2 }}{{16}}\).
C. \(\frac{{{a^3}\sqrt 2 }}{{24}}\).
D. \(\frac{{{a^3}\sqrt 2 }}{8}\).
Phương pháp:
- Thể tích khối chóp đều cạnh a: \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\)
- Tỉ lệ thể tích: \(\frac{{{V_{S.ABC}}}}{{{V_{S.A'B'C'}}}} = \frac{{SA}}{{SA'}}.\frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}}\)
Lời giải:
Đáp án đúng là: B
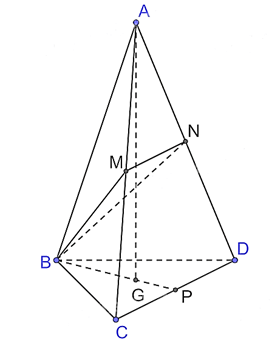
Gọi G là tâm của tam giác BCD. Vì tứ diện ABCD đều nên G là trọng tâm đồng thời là trực tâm của tam giác BCD và AG ⊥ (BCD).
Kẻ BG cắt CD tại P, suy ra P là trung điểm của CD và BG = 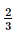 BP .
BP .
Xét tam giác BCD đều cạnh a có BP là đường cao nên BP =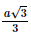 , suy ra BG =
, suy ra BG =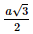
Xét tam giác ABG vuông tại G, có AG =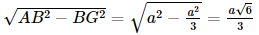
Vì tam giác BCD đều cạnh a nên 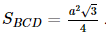
Ta có 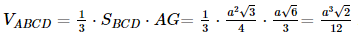
Vì M, N lần lượt là trung điểm của cạnh AC và cạnh AD nên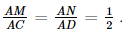
Có 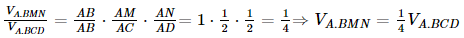
Mà VA.BMN + VB.CMND = VABCD nên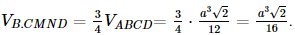
Bài 14 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = 1,AA' = 2\). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
A. \(\frac{{\sqrt 3 }}{2}\).
B. \(\frac{{\sqrt 3 }}{6}\).
C. \(\frac{{\sqrt 3 }}{4}\).
D. \(\frac{{\sqrt 3 }}{8}\).
Phương pháp:
Thể tích khối lăng trụ \(V = S.h\)
Lời giải:
Đáp án đúng là: A
Vì ABC.A'B'C' là lăng trụ tam giác đều nên AA' ⊥ (ABC) và tam giác ABC đều có cạnh bằng 1 nên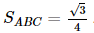
Do đó 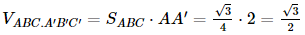 .
.
Bài 15 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AC' = \sqrt 3 \). Khoảng cách giữa hai đường thẳng \(AB'\) và \(BC'\) bằng
A. \(\frac{1}{3}\).
B. \(\frac{{\sqrt 3 }}{3}\).
C. \(\frac{{\sqrt 3 }}{2}\).
D. \(\frac{1}{2}\)
Phương pháp:
Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này đến mặt phẳng song song chứa đường thẳng kia
Lời giải:
Đáp án đúng là: B
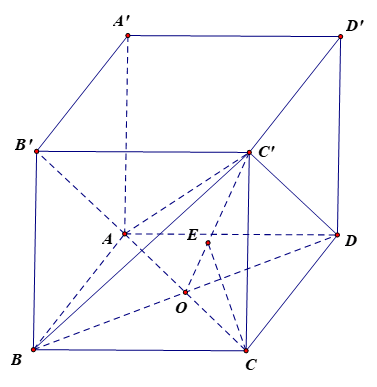
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD và AC ⊥ BD.
Có AD // B'C' và AD = B'C' (vì cùng song song và bằng BC) nên ADC'B' là hình bình hành, suy ra AB' // DC'. Do đó AB' // (BDC').
Khi đó d(AB', BC') = d(AB', (BDC')) = d(A, (BDC')) = d(C, (BDC')) .
Giả sử hình lập phương ABCD.A'B'C'D' có cạnh là a.
Xét tam giác ABC vuông tại B có AC=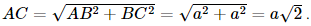
Vì CC' ⊥ (ABCD) nên CC' ⊥ AC hay tam giác ACC' vuông tại C.
Xét tam giác ACC' vuông tại C, có 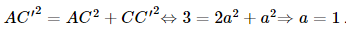
Do đó hình lập phương ABCD.A'B'C'D' có cạnh là 1 nên AC =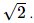
Vì O là trung điểm của AC nên CO =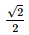
Có AC ⊥ BD, BD ⊥ AA' (do AA' ⊥ (ABCD)), suy ra BD ⊥ (ACC'A') mà BD ⊂ (BDC') nên (BDC') ⊥ (ACC'A') .
Kẻ CE ⊥ C'O tại E.
Vì (BDC') ⊥ (ACC'A'), (BDC') ∩ (ACC'A') = C'O mà CE ⊥ C'O nên CE ⊥ (BDC').
Khi đó d(C, (BDC')) = CE.
Xét tam giác C'CO vuông tại C, CE là đường cao có:

Vậy d(AB', BC') =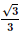
Bài 16 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho mẫu số liệu ghép nhóm về thu thập của các công nhân tại một doanh nghiệp lớn:
Nhóm chứa trung vị là
A. \([5;10)\).
B. \([10;15)\).
C. \([15;20)\).
D. \([20;25)\).
Phương pháp:
Trung vị là phần tử ở giữa sau khi sắp xếp tập dữ liệu theo thứ tự tăng dần.
Lời giải:
Đáp án đúng là: C
Cỡ mẫu là n = 7 + 18 + 35 + 57 + 28 = 145.
Giả sử x1; x2; …; x145 là mức thu nhập của 145 công nhân được sắp xếp theo thứ tự tăng dần. Khi đó trung vị là x73 mà x73 thuộc nhóm [15; 20). Vậy nhóm chứa trung vị là [15; 20).
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 99, 100, 101 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 97 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96 (11/01)
- BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
- Hoạt động thực hành trải nghiệm Hình học
- HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
- Bài tập cuối chương 9
- Bài 33. Đạo hàm cấp hai
- Bài 32. Các quy tắc tính đạo hàm
- Bài 31. Định nghĩa và ý nghĩa của đạo hàm
- CHƯƠNG IX. ĐẠO HÀM
- Bài tập cuối chương 8
- Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!