Giải SGK Toán 11 trang 56 Cánh Diều tập 1

Bài 1 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a)    \(5;\,\, - 0,5;\,\,0,05;\,\, - 0,005;\,\,0,0005\)

b)    \( - 9;\,\,3;\,\, - 1;\,\,\frac{1}{3};\,\, - \frac{1}{9}\)

c)    \(2;\,\,8;\,\,32;\,\,64;\,\,256\)

Phương pháp:

Dựa vào công thức cấp số nhân để xác định

Lời giải:

a)    Ta có:

\(\begin{array}{l} - 0,5:5 =  - 0,1\\0,05:\left( { - 0,5} \right) =  - 0,1\\ - 0,005:0,05 =  - 0,1\\0,0005:\left( { - 0,005} \right) =  - 0,1\end{array}\)

 Dãy số là cấp số nhân

b)    Ta có:

\(\begin{array}{l}3:\left( { - 9} \right) =  - \frac{1}{3}\\\left( { - 1} \right):3 =  - \frac{1}{3}\\\frac{1}{3}:\left( { - 1} \right) =  - \frac{1}{3}\\ - \frac{1}{9}:\left( {\frac{1}{3}} \right) =  - \frac{1}{3}\end{array}\)

 Dãy số là cấp số nhân

c)    Ta có:

\(\begin{array}{l}8:2 = 4\\32:8 = 4\\64:32 = 2\end{array}\)

 Dãy số không là cấp số nhân

Bài 2 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Chứng minh mỗi dãy số \(\left( {{u_n}} \right)\) với số hạng tổng quát như sau là cấp số nhân:

a)    \({u_n} =  - \frac{3}{4}{.2^n}\)

b)    \({u_n} = \frac{5}{{{3^n}}}\)

c)    \({u_n} = {\left( { - 0,75} \right)^n}\)

Phương pháp:

Dựa vào định nghĩa để chứng minh

Lời giải:

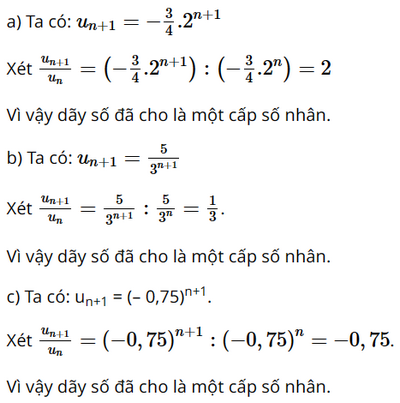
Bài 3 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Cho cấp số nhân \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} =  - 5\), công bội q = 2

a)    Tìm \({u_9}\)

b)    Số \( - 320\) là số hạng thứ bao nhiêu của cấp số nhân?

c)    Số 160 có phải là một số hạng của cấp số nhân trên không?

Phương pháp:

Dựa vào công thức tổng quát của cấp số nhân để xác định

Lời giải:

a)    \({u_9} = {u_1}.{q^{9 - 1}} = \left( { - 5} \right){.2^8} =  - 1280\)

b)    Ta có: \( - 320 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 64 \Leftrightarrow n = 7\)

 \( - 320\) là số hạng thứ 7 của cấp số nhân

c)    Ta có: \(160 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} =  - {2^5}\)

 160 không là số hạng của cấp số nhân

Bài 4 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3;{u_3} = \frac{{27}}{4}\)

a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên

b) Tính tổng 10 số hạng đầu của cấp số nhân trên

Phương pháp:

Dựa vào công thức tổng quát và tính tổng của cấp số nhân để xác định

Lời giải:

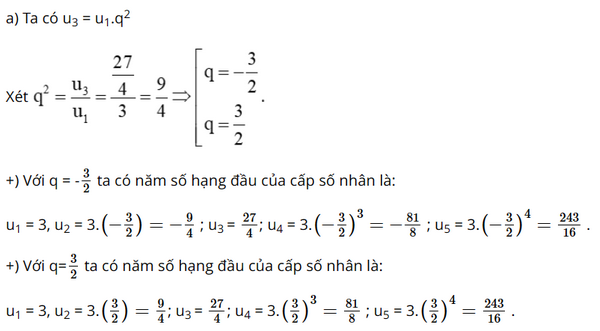
Bài 5 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi \({u_n}\) là số dân của tỉnh đó sau n năm. Giả sử tỉ lệ tăng dân số là không đổi.

a)    Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020

b)    Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020

Phương pháp:

Dựa vào công thức cấp số nhân để viết công thức tính dân số

Lời giải:

a)    Công thức tính dân số của tỉnh đó: \({S_n} = {u_1}{.1,01^n}\)

b)    Dân số của tính đó sau 10 năm:

\({S_{10}} = {2.1,01^{10}} \approx 2,21\) (triệu dân)

Bài 6 trang 56 SGK Toán 11 tập 1 - Cánh Diều

Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị của ô tô giảm đi 4% (so với năm trước đó).

a)    Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng

b)    Viết công thức tính giá trị của ô tô sau n năm sử dụng

c)    Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Phương pháp:

Dựa vào cấp số nhân để tính

Lời giải:

a) Sau 1 năm giá trị của ô tô còn lại là:

u₁ = 800 – 800.4% = 800.(1 – 4%) = 768 (triệu đồng).

Sau 2 năm giá trị của ô tô còn lại là:

u₁ = 800.(1 – 4%) – 800.(1 – 4%).4% = 800.(1 – 4%)² = 737,28 (triệu đồng).

b) Gọi u_n là giá trị của ô tô sau n năm sử dụng.

Dãy số (u_n) tạo thành một cấp số nhân với số hạng đầu là giá trị đầu của ô tô là u₀ = 800 triệu đồng và công bội q = 1 – 4%.

Khi đó công thức tổng quát để tính u_n = 800.(1 – 4%)ⁿ.

c) Sau 10 năm sử dụng giá trị của ô tô còn lại là:

u₁₀ = 800.(1 – 4%)¹⁰ ≈ 531,87 (triệu đồng).

Bài 7 trang 56 SGK Toán 11 tập 1 - Cánh Diều

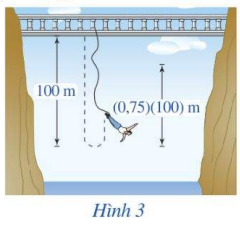
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thể cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống.

Phương pháp:

Dựa vào công thức cấp số nhân để xác định

Lời giải:

Quãng đường người đó đi được sau n lần kéo là: \(100.{\left( {1 - 0,25} \right)^n}\)

Quãng đường người đó đi được sau 10 lần kéo là: \(100.{\left( {1 - 0,25} \right)^{10}} \approx 5,63\,\,\left( m \right)\)

 Sachbaitap.com