Giải SGK Toán 11 trang 64, 65 Cánh Diều tập 1

Bài 1 trang 64 SGK Toán 11 tập 1 - Cánh Diều

Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\) với \({u_n} = 3 + \frac{1}{n};{v_n} = 5 - \frac{2}{{{n^2}}}.\) Tính các giới hạn sau:

a) \(\lim {u_n},\lim {v_n}.\)

b) \(\lim \left( {{u_n} + {v_n}} \right),\lim \left( {{u_n} - {v_n}} \right),\lim \left( {{u_n}.{v_n}} \right),\lim \frac{{{u_n}}}{{{v_n}}}.\)

Phương pháp:

Sử dụng định lí về giới hạn hữu hạn kết hợp với một số giới hạn cơ bản.

Định nghĩa dãy số có giới hạn hữu hạn.

Dãy số \(\left( {{u_n}} \right)\)có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a\) hay \({u_n} \to a\) khi  \(n \to  + \infty \) hay \(\lim {u_n} = a\).

Lời giải:

a) \(\begin{array}{l}\lim {u_n} = \lim \left( {3 + \frac{1}{n}} \right) = \lim 3 + \lim \frac{1}{n} = 3 + 0 = 3\\\lim {v_n} = \lim \left( {5 - \frac{2}{{{n^2}}}} \right) = \lim 5 - \lim \frac{2}{{{n^2}}} = 5 - 0 = 5\end{array}\)

b)

\(\begin{array}{l}\lim \left( {{u_n} + {v_n}} \right) = \lim {u_n} + \lim {v_n} = 3 + 5 = 8\\\lim \left( {{u_n} - {v_n}} \right) = \lim {u_n} - \lim {v_n} = 3 - 5 =  - 2\\\lim \left( {{u_n}.{v_n}} \right) = \lim {u_n}.\lim {v_n} = 3.5 = 15\\\lim \frac{{{u_n}}}{{{v_n}}} = \frac{{\lim {u_n}}}{{\lim {v_n}}} = \frac{3}{5}\end{array}\)

Bài 2 trang 65 SGK Toán 11 tập 1 - Cánh Diều

Tính các giới hạn sau:

a) \(\lim \frac{{5n + 1}}{{2n}};\)                  

b) \(\lim \frac{{6{n^2} + 8n + 1}}{{5{n^2} + 3}};\)                           

c) \(\lim \frac{{\sqrt {{n^2} + 5n + 3} }}{{6n + 2}};\)

d) \(\lim \left( {2 - \frac{1}{{{3^n}}}} \right);\)           

e) \(\lim \frac{{{3^n} + {2^n}}}{{{{4.3}^n}}};\)                               

g) \(\lim \frac{{2 + \frac{1}{n}}}{{{3^n}}}.\)

Phương pháp:

Sử dụng định lí về giới hạn hữu hạn kết hợp với một số giới hạn cơ bản.

Định nghĩa dãy số có giới hạn hữu hạn.

Dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to  + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to  + \infty } {u_n} = a\) hay \({u_n} \to a\) khi  \(n \to  + \infty \) hay \(\lim {u_n} = a\).

Lời giải:

Bài 3 trang 65 SGK Toán 11 tập 1 - Cánh Diều

a) Tính tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right),\) với \({u_1} = \frac{2}{3},q =  - \frac{1}{4}.\)

b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.

Phương pháp:

Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).

Lời giải:

a) \(S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{2}{3}}}{{1 - \frac{{ - 1}}{4}}} = \frac{8}{{15}}\)

b) \(1,\left( 6 \right) = \frac{5}{3}\)

Bài 4 trang 65 SGK Toán 11 tập 1 - Cánh Diều

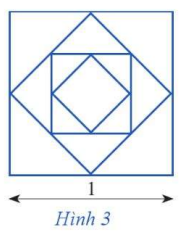
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. 

a) Tính diện tích \({S_n}\)  của hình vuông được tạo thành ở bước thứ n;

b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. 

Phương pháp:

Sử dụng công thức tính tổng n số hạng đầu của cấp số nhân \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\)

Tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).

Lời giải:

Bài 5 trang 65 SGK Toán 11 tập 1 - Cánh Diều

Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).

(Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)

Gọi \({u_n}\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n. 

a) Tìm số hạng tổng quát \({u_n}\) của dãy số \(\left( {{u_n}} \right)\). 

b) Chứng minh rằng \(\left( {{u_n}} \right)\) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g. 

Phương pháp:

 Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\)

Lời giải:

a) Sau một chu kì bán rã \({u_1} = 1.\frac{1}{2} = \frac{1}{2}\left( {kg} \right)\)

Sau hai chu kì bán rã \({u_2} = \frac{1}{2}.{u_1} = \frac{1}{{{2^2}}}\left( {kg} \right)\)

…

Vậy sau n chu kì bán rã \({u_n} = \frac{1}{{{2^n}}}\)

b) \(\lim {u_n} = \lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\)

c) Đổi \({10^{ - 6}}g = {10^{ - 9}}kg\)

Vì chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g nên ta có

\({u_n} < {10^{ - 9}} \Leftrightarrow \frac{1}{{{2^n}}} < {10^{ - 9}} \Leftrightarrow {2^n} > {10^9} \Leftrightarrow n > {\log _2}{10^9} \approx 29,9\)

Vậy sau 30 chu kì là 30.24 000 = 720 000 năm thì khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.

Bài 6 trang 65 SGK Toán 11 tập 1 - Cánh Diều

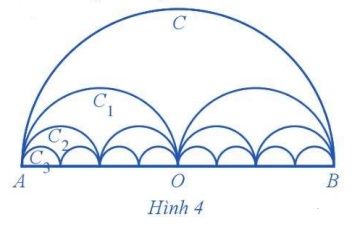
Gọi C là nửa đường tròn đường kính AB = 2R, C₁  là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2},\), C₂  là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4},...\) 

Gọi p_n  là độ dài của C_n, S_n  là diện tích hình phẳng giới hạn bởi C_n  và đoạn thẳng AB. 

a) Tính p_n, S_n. 

b) Tìm giới hạn của các dãy số (p_n) và (S_n). 

Phương pháp:

Chu vi hình tròn \(C = \pi d\)

Diện tích hình tròn \(S = \pi {R^2}\)

Lời giải:

a) Vì C_n là nửa đường tròn đường kính \(\frac{{AB}}{{{2^n}}}\) nên ta có \({p_n} = \frac{1}{2}{.2^n}.\frac{{AB}}{{{2^n}}}.\pi  = {2^n}.\frac{R}{{{2^n}}}.\pi  = \pi R\)

Đường kính \(\frac{{AB}}{{{2^n}}} = \frac{{2R}}{{{2^n}}}\) nên bánh kính \(\frac{R}{{{2^n}}}\)

\({S_n} = {2^n}.{\left( {\frac{R}{{{2^n}}}} \right)^2}.\frac{\pi }{2} = \frac{{\pi {R^2}}}{2}.\frac{1}{{{2^n}}} = \frac{{\pi {R^2}}}{{{2^{n + 1}}}}\)

b)  \(\begin{array}{l}\lim {p_n} = \lim \left( {\pi R} \right) = \pi R\\\lim {S_n} = \lim \frac{{\pi {R^2}}}{{{2^{n + 1}}}} = \lim \left[ {\frac{{\pi {R^2}}}{2}.{{\left( {\frac{1}{2}} \right)}^n}} \right] = \lim \frac{{\pi {R^2}}}{2}.\lim {\left( {\frac{1}{2}} \right)^n} = 0\end{array}\)

Sachbaitap.com