Giải SGK Toán 11 trang 77 Cánh Diều tập 1

Bài 1 trang 77 SGK Toán 11 tập 1 - Cánh Diều

Dùng định nghĩa xét tính liên tục của hàm số \(f\left( x \right) = 2{x^3} + x + 1\) tại điểm \(x = 2.\)

Phương pháp:

Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải:

Hàm số \(f\left( x \right) = 2{x^3} + x + 1\) xác định trên \(\mathbb{R}\).

Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left( {2{x^3} + x + 1} \right) = {2.2^3} + 2 + 1 = 17\\f\left( 2 \right) = {2.2^3} + 2 + 1 = 17\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\end{array}\)

Do đó hàm số liên tục tại x = 2.

Bài 2 trang 77 SGK Toán 11 tập 1 - Cánh Diều

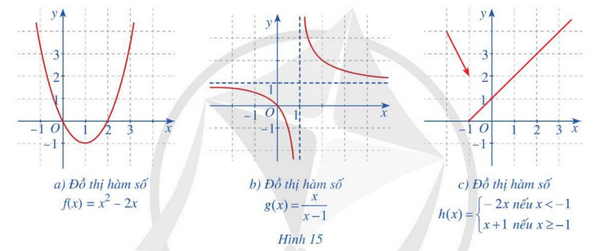
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Phương pháp:

- Các hàm đa thức liên tục trên \(\mathbb{R}\)

- Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng

- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải:

Bài 3 trang 77 SGK Toán 11 tập 1 - Cánh Diều

Bạn Nam cho rằng: “Nếu hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0},\) còn hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0},\) thì hàm số \(y = f\left( x \right) + g\left( x \right)\) không liên tục tại \({x_0}\)”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Phương pháp:

Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải:

Theo em ý kiến của bạn Nam là đúng.

Ta có: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne g\left( {{x_0}} \right)\)

Do đó \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) + \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne f\left( {{x_0}} \right) + g\left( {{x_0}} \right)\)

Vì vậy hàm số không liên tục tại x₀.

Bài 4 trang 77 SGK Toán 11 tập 1 - Cánh Diều

Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) \(f\left( x \right) = {x^2} + \sin x;\) 

b) \(g\left( x \right) = {x^4} - {x^2} + \frac{6}{{x - 1}};\)         

c) \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}.\)

Phương pháp:

- Các hàm đa thức, hàm số lượng giác \(y = \sin x,y = \cos x\) liên tục trên \(\mathbb{R}\)

- Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng

- Định lí tính liên tục của tổng của hai hàm số liên tục: Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó các hàm số \(y = f(x) \pm g(x)\)và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).

Lời giải:

Bài 5 trang 77 SGK Toán 11 tập 1 - Cánh Diều

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1,\,\,x \ne 4\\2a + 1,\,\,x = 4\end{array} \right.\)

a) Với a = 0, xét tính liên tục của hàm số tại x = 4.

b) Với giá trị nào của a thì hàm số liên tục tại x = 4?

c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?

Phương pháp:

- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

- Các hàm đa thức liên tục trên \(\mathbb{R}\)

Lời giải:

a) Với a = 0, tại x = 4, ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2.0 + 1 = 1\\ \Rightarrow \mathop {\lim }\limits_{x \to 4} f\left( x \right) \ne f\left( 4 \right)\end{array}\)

Do đó hàm số không liên tục tại x = 4.

b) Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2a + 1\end{array}\)

Để hàm số liên tục tại x = 4 thì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = f\left( 4 \right)\)

\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;21{\rm{ }} = {\rm{ }}2a{\rm{ }} + {\rm{ }}1}\\{ \Leftrightarrow \;2a{\rm{ }} = {\rm{ }}20}\\{ \Leftrightarrow \;a{\rm{ }} = {\rm{ }}10}\end{array}\)

Vậy với a = 10 thì hàm số liên tục tại x = 4.

c) TXĐ: \(\mathbb{R}\)

Với \(x\; \in \;\left( {-{\rm{ }}\infty ;{\rm{ }}4} \right)\) có \(f\left( x \right) = {x^2} + x + 1\) liên tục với mọi x thuộc khoảng này.

Với \(x\; \in \;\left( {4;{\rm{ }} + \infty } \right)\) có \(f\left( x \right) = 2a + 1\) liên tục với mọi x thuộc khoảng này.

Do đó hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) khi hàm số \(f\left( x \right)\) liên tục tại điểm x = 4 khi a = 10.

Vậy với a = 10 hàm số liên tục trên tập xác định của nó.

Bài 6 trang 77 SGK Toán 11 tập 1 - Cánh Diều

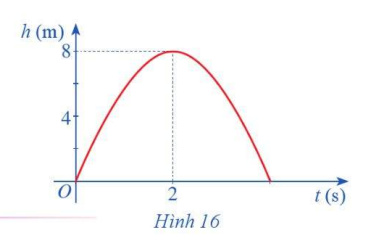
Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) =  - 2{t^2} + 8t.\)

a) Chứng tỏ hàm số \(h\left( t \right)\) liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right).\)

Phương pháp:

Các hàm đa thức liên tục trên \(\mathbb{R}\)

Lời giải:

Sachbaitap.com