Giải SGK Toán 8 Cánh Diều tập 2 trang 81, 82

Bài 1 trang 81 SGK Toán 8 - Cánh Diều tập 2

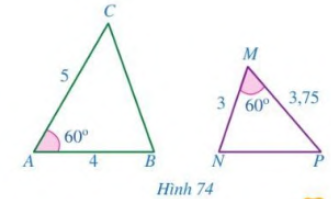
Cho Hình 74.

a) Chứng minh \(\Delta ABC \backsim \Delta MNP\)

b) Góc nào của tam giác MNP bằng góc B?

c) Góc nào của tam giác ABC bằng góc P?

Phương pháp:

a) Sử dụng trường hợp đồng dạng thứ hai để chứng minh hai tam giác đồng dạng.

b) Sử dụng định nghĩa hai tam giác đồng dạng để tìm ta các góc bằng nhau.

c) Sử dụng định nghĩa hai tam giác đồng dạng để tìm ta các góc bằng nhau.

Lời giải:

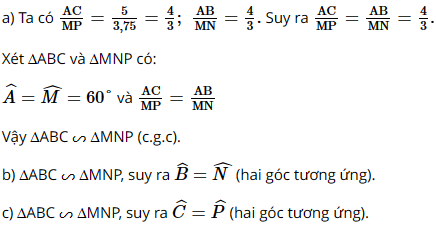
Bài 2 trang 82 SGK Toán 8 - Cánh Diều tập 2

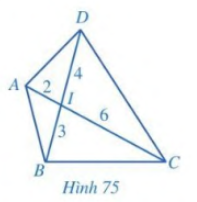
Cho Hình 75, chứng minh:

a) \(\Delta IAB \backsim \Delta IDC\)

b) \(\Delta IAD \backsim \Delta IBC\)

Phương pháp:

Tìm ra các tỉ số bằng nhau của các cạnh và chứng minh các cặp tam giác đồng dạng theo trường hợp đồng dạng thứ hai.

Lời giải:

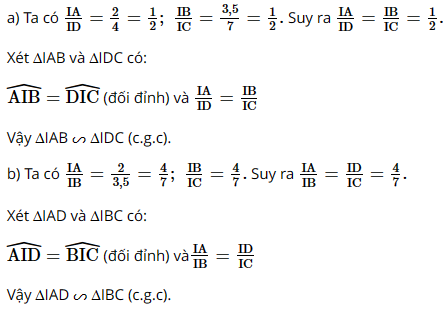
Bài 3 trang 82 SGK Toán 8 - Cánh Diều tập 2

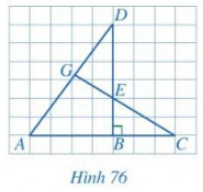
Cho Hình 76, biết \(AB = 4,\,\,BC = 3,\,\,BE = 2,\,\,BD = 6\). Chứng minh:

a) \(\Delta ABD \backsim \Delta EBC\)

b) \(\widehat {DAB} = \widehat {DEG}\)

c) Tam giác DGE vuông

Phương pháp:

a) Chứng minh hai tam giác đồng dạng bằng trường hợp đồng dạng thứ hai.

b) Từ hai tam giác đồng dạng đã chứng minh ở câu a suy ra các cặp góc bằng nhau.

c) Chứng minh \(\widehat {DGE} = 90^\circ \)

Lời giải:

Bài 4 trang 82 SGK Toán 8 - Cánh Diều tập 2

Cho Hình 77, chứng minh

a) \(\widehat {ABC} = \widehat {BED}\)

b) \(BC \bot BE\)

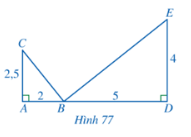
Hình 77

Phương pháp:

a) Chứng minh \(\Delta ABC \backsim \Delta DEB\) từ đó suy ra cặp góc bằng nhau.

b) Chứng minh \(\widehat {CBE} = 90^\circ \)

Lời giải:

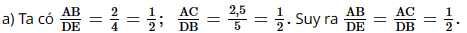
Xét ∆ABC và ∆DEB có:

Bài 5 trang 82 SGK Toán 8 - Cánh Diều tập 2

Cho \(\Delta ABC \backsim \Delta MNP\).

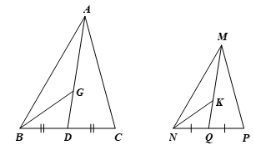
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).

b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).

Phương pháp:

Sử dụng định nghĩa tam giác đồng dạng để tìm điểm P.

Lời giải:

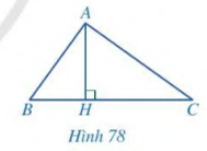
Bài 6 trang 82 SGK Toán 8 - Cánh Diều tập 2

Cho Hình78, biết \(A{H^2} = BH.CH\). Chứng minh:

a)      \(\Delta HAB \backsim \Delta HCA\)

b)     Tam giác ABC vuông tại A.

Phương pháp:

a) Từ đẳng thức đã cho, suy ra tỉ lệ các đoạn thẳng rồi chứng minh hai tam giác bằng nhau theo trường hợp thứ hai.

b) Chứng minh \(\widehat {BAC} = 90^\circ \)

Lời giải:

Bài 7 trang 82 SGK Toán 8 - Cánh Diều tập 2

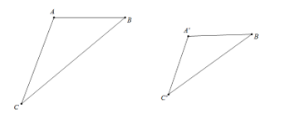
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thỏa mãn \(AB = 20m,{\rm{ }}AC = 0m,\;\,\,\widehat {BAC} = 135^\circ \)

Bạn Vy làm như sau: Vẽ tam giác A'B'C' có \(A'B' = 2cm,{\rm{ }}A'C' = 5cm,\;\widehat {B'A'C'} = 135^\circ \). Bạn Vy lấy thước đo khoảng cách giữa hai điểm B', C' và nhận được kết quả \(B'C'\; \approx \;6,6cm\). Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.

Phương pháp:

Sử dụng định nghĩa hai tam giác đồng dạng để giải thích.

Lời giải:

Đổi A’B’ = 2 cm = 0,02 m;

      A’C’ = 5 cm = 0,05 m;

B’C’ = 6,6 cm = 0,066 m.

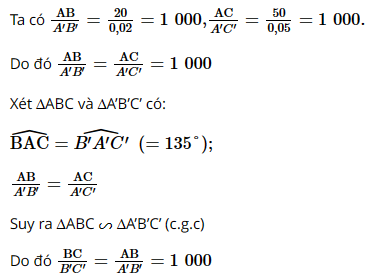
Nên BC = 1 000 . B’C’ = 1 000 . 0,066 = 66 (m).

Vậy khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66m. 

Sachbaitap.com