Giải Toán 7 trang 10, 11 Cánh Diều tập 1
Giải bài 1, 2, 3 trang 10, bài 4, 5, 6, 7, 8, 9, 10 trang 11 SGK Toán lớp 7 cánh diều tập 1 - Bài 1. Tập hợp Q các số hữu tỉ. Bài 3.Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
Bài 1 trang 10 SGK Toán 7 tập 1 - Cánh Diều
Các số 13, -29; -2,1; 2,28; \(\frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ không? Vì sao?
Phương pháp:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Lời giải:
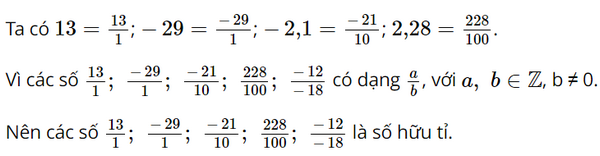
Bài 2 trang 10 SGK Toán 7 tập 1 - Cánh Diều
Chọn kí hiệu thích hợp cho dấu “?”
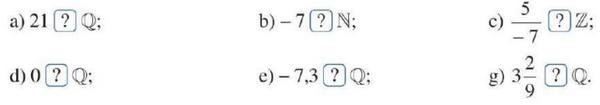
Phương pháp:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Dùng kí hiệu “\( \in \)” nếu số thuộc tập hợp
Dùng kí hiệu “\( \notin \)” nếu số không thuộc tập hợp
Lời giải:

Bài 3 trang 10 SGK Toán 7 tập 1 - Cánh Diều
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu \(a \in \mathbb{N}\) thì \(a \in \mathbb{Q}\)
b) Nếu \(a \in \mathbb{Z}\) thì \(a \in \mathbb{Q}\)
c) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{N}\)
d) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{Z}\)
e) Nếu \(a \in \mathbb{N}\) thì \(a \notin \mathbb{Q}\)
g) Nếu \(a \in \mathbb{Z}\) thì \(a \notin \mathbb{Q}\)
Phương pháp:
Tập hợp các số hữu tỉ \(\mathbb{Q} = \left\{ {\frac{a}{b};\,a,b \in \mathbb{Z};\,b \ne 0} \right\}\)
\(\mathbb{N} = \left\{ {0;\,1;\,2;...} \right\}\)
\(\mathbb{Z} = \left\{ {..., - 2; - 1;0;\,1;\,2;...} \right\}\)
Lời giải:
a) Mọi số tự nhiên a bất kỳ đều biểu diễn được dưới dạng phân số ![]()
Khi đó, nếu a là số tự nhiên thì a cũng là số hữu tỉ.
Do đó phát biểu “Nếu a∈ℕ">a∈ℕ thì a∈ℚ">a∈ℚ” là đúng.
b) Mọi số nguyên a bất kỳ đều biểu diễn được dưới dạng phân số ![]() .
.
Khi đó, nếu a là số nguyên thì a cũng là số hữu tỉ.
Do đó phát biểu “Nếu
Ví dụ: 2 vừa là số hữu tỉ vừa là số tự nhiên.
Nếu a là số hữu tỉ thì a có thể không phải là số tự nhiên.
Ví dụ: ![]() là số hữu tỉ nhưng không phải là số tự nhiên.
là số hữu tỉ nhưng không phải là số tự nhiên.
Khi đó, nếu a là số hữu tỉ thì a chưa chắc là số tự nhiên.
Do đó phát biểu “Nếu a∈ℚ thì a∈ℕ” là sai.
d) Nếu a là số hữu tỉ thì a có thể là số nguyên.
Ví dụ: −5 vừa là số hữu tỉ vừa là số nguyên.
Nếu a là số hữu tỉ thì a có thể không phải là số nguyên.
Ví dụ: ![]() là số hữu tỉ nhưng không phải là số nguyên.
là số hữu tỉ nhưng không phải là số nguyên.
Khi đó, nếu a là số hữu tỉ thì a chưa chắc là số nguyên.
Do đó phát biểu “Nếu a∈ℚ thì a∈ℤ” là sai.
e) Mọi số tự nhiên a bất kỳ đều biểu diễn được dưới dạng phân số ![]()
Khi đó, nếu a là số tự nhiên thì a cũng là số hữu tỉ.
Do đó phát biểu “Nếu a∈ℕ thì a∉ℚ” là sai.
g) Mọi số nguyên a bất kỳ đều biểu diễn được dưới dạng phân số ![]()
Khi đó, nếu a là số nguyên thì a cũng là số hữu tỉ.
Do đó phát biểu “Nếu a∈ℤ thì a∉ℚ” là sai.
Vậy các phát biểu đúng là: a, b và các phát biểu sai là: c, d, e, g.
Bài 4 trang 11 SGK Toán 7 tập 1 - Cánh Diều
Quan sát trục số sau và cho biết các điểm A, B, C, D biểu diễn những số nào?

Phương pháp:
- Điểm biểu diễn số hữu tỉ a là điểm a.
- Quan vị trí các điểm A, B, C, D trên trục số và trả lời câu hỏi.
Lời giải:
Mỗi đoạn thẳng đơn vị được chia thành 7 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng ![]() đơn vị cũ).
đơn vị cũ).
* Đi theo ngược chiều dương với trục số, bắt đầu từ điểm 0:
- Điểm A chiếm 9 phần nên điểm A biểu diễn số ![]()
- Điểm B chiếm 3 phần nên điểm B biểu diễn số ![]()
* Đi theo chiều dương của trục số, bắt đầu từ điểm 0:
- Điểm C chiếm 2 phần nên điểm C biểu diễn số ![]()
- Điểm D chiếm 6 phần nên điểm D biểu diễn số ![]()
Vậy các điểm A, B, C, D lần lượt biểu diễn các số ![]()
Bài 5 trang 11 SGK Toán 7 tập 1 - Kết nối tri thức
Tìm số đối của mỗi số sau: \(\frac{9}{{25}};\,\frac{{ - 8}}{{27}};\, - \frac{{15}}{{31}};\frac{5}{{ - 6}};\,3,9;\, - 12,5\).
Phương pháp:
Số đối của số x kí hiệu là: -x
Lời giải:
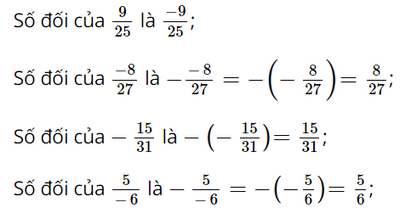
Số đối của 3,9 là −3,9.
Số đối của −12,5 là − (−12,5) = 12,5.
Bài 6 trang 11 SGK Toán 7 tập 1 - Cánh Diều
Biểu diễn số đối của mỗi số đã cho trên trục số sau:

Phương pháp:
Số đối của một số a nằm bên kia số 0 và cách 0 một khoảng bằng với khoảng cách từ điểm a đến điểm 0.
Lời giải:
Số đối của ![]()
Số đối của ![]()
Số đối của 0 là 0;
Số đối của 1 là − 1;
Số đối của ![]()
Biểu diễn các số ![]()

Bài 7 trang 11 SGK Toán 7 tập 1 - Cánh Diều
So sánh:
a)\(2,4\) và \(2\frac{3}{5}\);
b) \( - 0,12\) và \( - \frac{2}{5}\)
c)\(\frac{{ - 2}}{7}\) và \( - 0,3\).
Phương pháp:
Đưa các số về dạng hai phân số cùng mẫu rồi so sánh.
Lời giải:
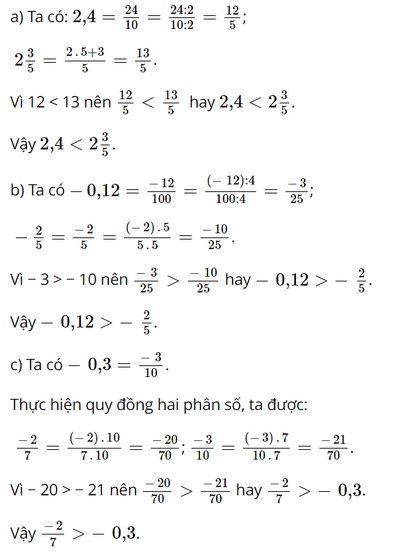
Bài 8 trang 11 SGK Toán 7 tập 1 - Cánh Diều
a) Sắp xếp các số sau theo thứ tự tăng dần: \(\frac{{ - 3}}{7};\,0,4;\, - 0,5;\,\frac{2}{7}\).
b) Sắp xếp các số sau theo thứ tự giảm dần: \(\frac{{ - 5}}{6};\, - 0,75;\, - 4,5;\, - 1\).
Phương pháp:
- Đưa các số về các phân số có cùng mẫu số để so sánh
- Sắp xếp các phân số theo thứ tự.
Lời giải:
![]()
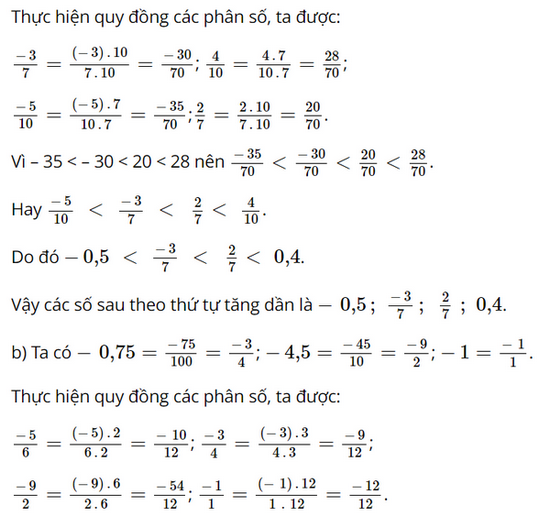
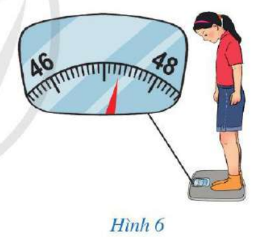
Bài 9 trang 11 SGK Toán 7 tập 1 - Cánh Diều
Hình 4 mô tả một chiếc cân khối lượng, ở đó các vạch ghi 46 và 48 lần lượt ứng với các số đo 46 kg và 48 kg. Khi nhìn vị trí mà chiếc kim chỉ vào, bạn Minh đọc số đo là 47,15 kg, bạn Dương đọc số đo là 47,3 kg, bạn Quân đọc số đo là 47,65 kg. Bạn nào đã đọc đúng số đo? Vì sao?
Phương pháp:
Quan sát độ chia nhỏ nhất của chiếc cân và quan sát xem chiếc kim chỉ vào số bao nhiêu
Lời giải:
Từ vạch ghi 46 đến vạch ghi 48 lần lượt ứng với các số đo 46 kg và 48 kg thì vạch đậm chính giữa hai vạch này chỉ số đo 47 kg.
Từ vạch chỉ số đo 47 kg đến vạch chỉ số đo 48 kg được chia thành 10 đoạn nhỏ nên mỗi đoạn tương ứng với 0,1 kg.
Do đó, chiếc cân chỉ 47,3 kg.
Vậy bạn Dương đã đọc đúng số đo.
Bài 10 trang 11 SGK Toán 7 tập 1 - Cánh Diều
Cô Hạnh dự định xây tầng hầm cho ngôi nhà của gia đình. Một công ty tư vấn xây dựng đã cung cấp cho cô Hạnh lựa chọn một trong sáu số đo chiều cao của tầng hầm như sau: 2,3 m; 2,35 m; 2,4 m; 2,55 m; 2,5 m; 2,75 m. Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn \(\frac{{13}}{5}\)m để đảm bảo ánh sáng, thoáng đãng, cân đối về kiến trúc và thuận tiện trong sử dụng. Em hãy giúp cô Hạnh chọn đúng số đo chiều cao của tầng hầm.
Phương pháp:
Đổi chiều cao của tầng hầm ra số thập phân rồi so sánh với sáu số đo chiều cao được tư vấn.
=>Chọn chiều cao lớn hơn chiều cao của tầng hầm.
Lời giải:
Ta có ![]()
Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn ![]() hay chiều cao lớn hơn 2,6 m.
hay chiều cao lớn hơn 2,6 m.
Mà trong sáu lựa chọn mà công ty tư vấn xây dựng đã đưa ra cho cô Hạnh thì chỉ có chiều cao 2,75 m lớn hơn 2,6 m.
Vậy số đo chiều cao của tầng hầm cô Hạnh cần chọn là 2,75 m.
Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 7 - Toán 7 Cánh Diều
- Bài 13. Tính chất ba đường cao của tam giác - Toán 7 Cánh Diều
- Bài 12. Tính chất ba đường trung trực của tam giác - Toán 7 Cánh Diều
- Bài 11. Tính chất ba đường phân giác của tam giác - Toán 7 Cánh Diều
- Bài 10. Tính chất ba đường trung tuyến của tam giác - Toán 7 Cánh Diều
- Bài 9. Đường trung trực của một đoạn thẳng - Toán 7 Cánh Diều
- Bài 8. Đường vuông góc và đường xiên - Toán 7 Cánh Diều
- Bài 7. Tam giác cân - Toán 7 Cánh Diều
- Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc - Toán 7 Cánh Diều
- Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh - Toán 7 Cánh Diều
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
