Giải bài 1, 2, 3, 4, 5, 6 trang 98, 99 Sách bài tập Toán 6 tập 2 - Chân trời sáng tạo

Bài 1 trang 98 SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Bổ sung vào chỗ chấm để được các phát biểu đúng.

a) Góc là hình được tạo bởi ………………

b) Góc xOy có đỉnh là ……………… và hai cạnh là …………

c) Góc ……………… có đỉnh là M và hai cạnh là MN và MP.

phương pháp:

+ Góc là hình tạo bởi hai tia chung gốc

+ đỉnh của góc là gốc chung, còn hai cạnh của góc chính là hai tia.

Trả lời:

a) Góc là hình được tạo bởi hai tia chung gốc.

b) Góc xOy có đỉnh là O và hai cạnh là Ox và Oy.

c) Góc NMP có đỉnh là M và hai cạnh là MN và MP.

Bài 2 trang 98- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

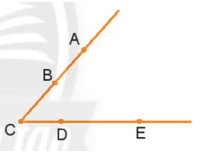
 Các góc nào có trong hình sau đây:

Hãy khoanh tròn các phương án phù hợp.

a) Góc ABC;

b) Góc ACD;

c) Góc ADC;

d) Góc BCD;

e) Góc EBD;

g) Góc AEB.

Phương pháp:

+ Góc là hình được tạo bởi hai tia chung gốc. Ví dụ góc AOB có đỉnh là O và hai tia là OA, OB.

Trả lời:

Dễ thấy:

a) Góc ABC là góc bẹt (đỉnh A, hai tia là BA, BC). Góc ABC có trong hình.

b) Góc ACD có đỉnh C, hai tia là CA và CD. Góc ACD có trong hình.

c) Góc ADC không có trong hình do không nối tia DA.

d) Góc BCD có đỉnh C, hai tia là CB và CD. Góc BCD có trong hình.

e) Góc EBD không có trong hình do không nối tia BE, BD.

g) Góc AEB không có trong hình do không nối tia EA, EB.

Do đó các góc có trong hình là: góc ABC, góc ACD, góc BCD.

Vậy các phương án phù hợp là: a), b), d).

Bài 3 trang 98- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

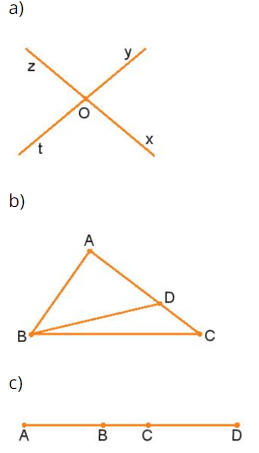
Hãy kể tên các góc có trong mỗi hình vẽ dưới đây:

Trả lời:

a)

Đỉnh chung: O

Các tia: Ox, Oy, Oz, Ot

Các góc tạo thành: xOy, xOz, xOt, yOz, yOt, zOt

b) Đỉnh A

Các tia: AB, AD, AC (trong đó tia AD và AC trùng nhau)

Góc tạo thành: BAD = BAC

Đỉnh B

Các tia: BA, BD, BC

Các góc tạo thành: ABD, ABC, DBC

Đỉnh C: BCD = BCA

Đỉnh D

Các tia: DA, DB, DC

Các góc tạo thành: ADB, BDC, ADC.

c) Đỉnh B:

Tia BA, BC (trùng với tia BD)

Các góc tạo thành: ABC

Đỉnh C:

Tia CD, CB (trùng với tia CA)

Các góc tạo thành: BCD

Bài 4 trang 98- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

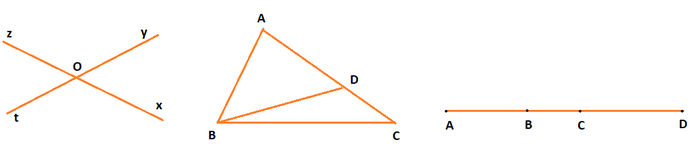
Mỗi hình dưới đây có bao nhiêu góc?

Phương pháp:

Bước 1: Tính số đỉnh chung được tạo thành. Với mỗi điểm chung có bao nhiêu tia.

Bước 2: Nếu đỉnh chung có n tia thì sẽ có: n(n-1) :2. Tỉnh tổng các góc được tạo thành.

Trả lời:

a) Số đỉnh chung: 1

Số tia: 4

Số góc tạo thành:4.3:2 = 6 góc

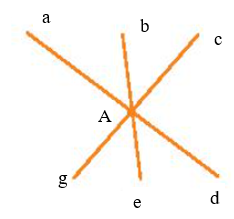
b) Số đỉnh chung: 1

Số tia: 6

Số góc tạo thành:6.5:2 = 15 góc

Bài 5 trang 99 - SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

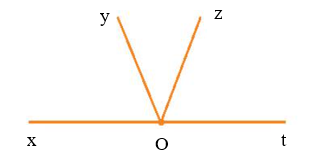
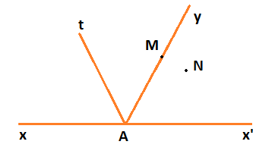
 Điểm M và điểm N là điểm trong của những góc nào trong hình vẽ dưới đây?

Phương pháp:

Nếu góc xAy không bẹt, điểm N là điểm trong của góc xAy nếu tia AN cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó.

Trả lời:

Trên tia Ax’, Ay, At, Ax lần lượt lấy các điểm B, C, D, E.

Nối BC, CD, DE, BD, EC và AB với nhau (như hình vẽ).

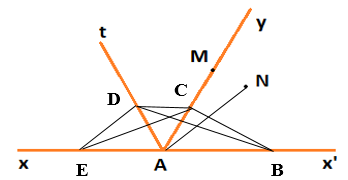
Nhận thấy:

+) AM cắt đoạn BD mà B ∈ Ax’, D ∈ At nên điểm M là điểm trong của ∠x'At.

+) AN cắt đoạn BC mà B ∈ Ax’, C ∈ Ay nên điểm N là điểm trong của ∠x'Ay.

+) AN cắt đoạn BD mà B ∈ Ax’, D ∈ At nên điểm N là điểm trong của ∠x'At.

Vậy M là điểm trong của ∠x'At , N là điểm trong của ∠x'Ay và ∠x'At.

Bài 6 trang 99- SBT Toán 6 tập 2 - Chân trời sáng tạo

Câu hỏi:

Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó.

Phương pháp:

Bước 1: Liệt kê các trường hợp có thể xảy ra của 3 đường thẳng

Bước 2: Mỗi trường hợp, để đếm số góc ta làm như sau: Đếm số đỉnh chung, mỗi đỉnh chung đó có bao nhiêu tia (giải sử là n) thì đỉnh chung đó tạo thành n(n-1):2 góc.

Trả lời:

Vẽ hai đường thẳng trước, có hai khả năng xảy ra:

* Khả năng 1: Hai đường thẳng đó song song với nhau.

Ta tiếp tục vẽ thêm một đường thẳng thứ ba song song hoặc cắt cả hai đường thẳng kia.

- Trường hợp 1: Đường thẳng thứ ba song song cả hai đường thẳng kia thì ba đường thẳng này không có giao điểm nào.

Vì ba đường thẳng này không có giao điểm nào nên không có góc nào tạo ra trong trường hợp này.

- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia thì ta có hai giao điểm A và B.

Từ hai điểm gốc A, B, đặt các tia Aa, Ab, Ac, Bd, Be, Bg (như hình vẽ).

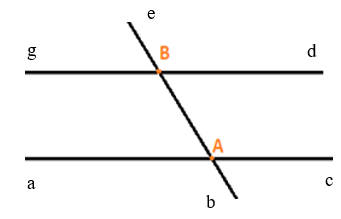
Các góc tạo thành: ∠aAb, ∠bAc, ∠aAe, ∠eAc, ∠aAc, ∠dBe, ∠eBg, ∠dBb, ∠bBg, ∠dBg, ∠bAe, ∠bBe.

Vậy hình trên có 12 góc.

* Khả năng 2: Hai đường thẳng đó cắt nhau cắt nhau tại điểm A.

Ta tiếp tục vẽ thêm một đường thẳng thứ ba cắt cả hai đường thẳng kia.

- Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A.

Từ điểm gốc A, đặt các tia Aa, Ab, Ac, Ad, Ae, Ag (như hình vẽ).

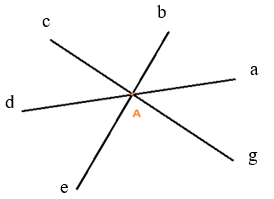
Các góc tạo thành: ∠aAb, ∠bAc, ∠cAd, ∠dAe, ∠eAg, ∠gAa, ∠aAc, ∠cAe, ∠eAa, ∠aAd, ∠bAd, ∠dAg, ∠gAb, ∠bAe, ∠cAg      .

Vậy hình trên có 15 góc.

- Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).

Từ ba điểm gốc A, B, C đặt các tia Ah, Ak, Bp, Bq, Cm, Cn (như hình vẽ).

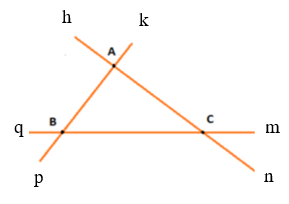
Các góc tạo thành: ∠hAk, ∠kAn, ∠hAp, ∠pAn, ∠hAn, ∠pAk, ∠pBq, ∠pBm, ∠qBk, ∠kBm, ∠mBq, ∠pBk, ∠mCn, ∠mCh, ∠nCq, ∠qCh, ∠nCh, ∠mCq      .

Vậy hình trên có 18 góc.

*Nhận xét: 

- Hình thứ nhất: Ba đường thẳng không có điểm chung nên không có góc nào tạo ra. 

- Hình thứ hai: 2 đỉnh chung, mỗi đỉnh có 4 tia.

Vậy số góc tạo thành là 2 . 4 . 3 : 2 = 12 góc.

- Hình thứ ba: 1 đỉnh chung, có 6 tia.

Vậy số góc tạo thành là 6 . 5 : 2 = 15 (góc).

- Hình thứ tư: 3 đỉnh chung, mỗi đỉnh có 4 tia.

Vậy số góc tạo thành là 3 . 4 . 3 : 2 = 18 (góc).

Vậy nếu đỉnh chung có n tia thì:

Tổng số các góc được tạo thành là:  n . (n − 1) : 2 (góc). 

Sachbaitap.com