Bài 27, 28, 29, 30, 31, 32, 33, 34, 35 trang 113, 114, 115, 116 SGK Toán 8 tập 2 -Thể tích của hình lăng trụ đứng- luyện tập
Bài 27 trang 113, bài 28, 29, 30 trang 114, bài 31, 32, 33 trang 115, bài 34, 35 trang 116 SGK Toán 8 tập 2 bài Thể tích của hình lăng trụ đứng - luyện tập. Bài 35 Đáy của một lăng trụ đứng là tứ giác, các kích thước cho theo hình 115.
- Bài 36, 37, 38, 39 trang 118, 119 SGK Toán 8 tập 2 - Hình chóp đều và hình chóp cụt...
- Bài 40, 41, 42, 43 trang 121 SGK Toán 8 tập 2 - Diện tích xung quanh của hình chóp đều
- Bài 44, 45, 46, 47, 48, 49, 50 trang 123, 124, 125 SGK Toán 8 tập 2 - Thể tích của...
- Bài 51, 52, 53, 54, 55, 56, 57, 58 trang 127, 128, 129 SGK Toán 8 tập 2 - Ôn tập...
Bài 27 trang 113 SGK Toán lớp 8 tập 2
Câu hỏi:
Quan sát hình 108 rồi điền số thích hợp vào các ô trống ở bảng sau:
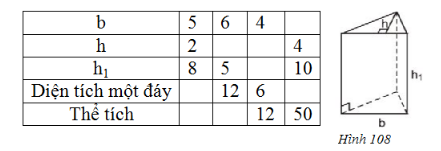
Lời giải:
Ta có : Diện tích đáy: \(S = \dfrac{1}{2}b.h\).
Thể tích \( V= S.h_1\)
+ Ở cột 2 : \(S = \dfrac{1}{2} b.h = \dfrac{1}{2}. 5.2 = 5\)
\( V= S.h_1 = 5. 8 = 40\)
+ Ở cột 3 : \(S = \dfrac{1}{2}. b.h\)\(\, \Rightarrow h =\dfrac{2.S}{b} =\dfrac{2.12}{6}= 4\)
\( V= S.h_1 = 12. 5 = 60\)
+ Ở cột 4: \(h = \dfrac{2.S}{b} = \dfrac{2.6}{4}= 3 \)
\(V = S.h_1 \Rightarrow h_1 =\dfrac{V}{S} =\dfrac{12}{6}= 2\)
+ Ở cột 5: \(V = S.h_1 \Rightarrow S=\dfrac{V}{h_1} =\dfrac{50}{10}= 5\)
\(S =\dfrac{1}{2} b.h \Rightarrow b = \dfrac{2.S}{h} = \dfrac{2.5}{4} = 2,5\)
Vậy có kết quả sau khi điền vào bảng sau là:
|
b(cm) |
5 |
6 |
4 |
2,5 |
|
h(cm) |
2 |
4 |
3 |
4 |
|
h1(cm) |
8 |
5 |
2 |
10 |
|
Diện tích một đáy(\(cm^2\)) |
5 |
12 |
6 |
5 |
|
thể tích |
40 |
60 |
12 |
50 |
Bài 28 trang 114 SGK Toán lớp 8 tập 2
Câu hỏi:
Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác (h.109). Hãy tính dung tích của thùng.
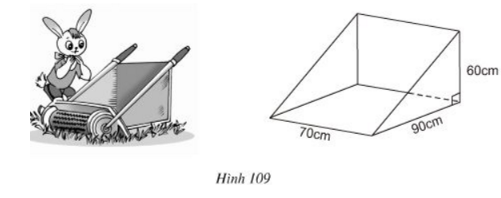
Lời giải:
Lăng trụ đứng tam giác có đáy là tam giác vuông nên diện tích đáy là :
\( S = \dfrac{1}{2}. 60.90 = 2700 (cm^2) \)
Thể tích lăng trụ là:
\(V = S. h = 2700.70 = 189000 (cm^3) \)
Vậy dung tích của thùng là \( 189000 (cm^3) \).
Bài 29 trang 114 SGK Toán lớp 8 tập 2
Câu hỏi:
Các kích thước của một bể bơi được cho trên hình 110 (mặt nước có dạng hình chữ nhật). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?

Lời giải:
Bể bơi được chia thành hai phần: phần hình hộp chữ nhật với các kích thước là \(10m, \;25m,\; 2m\) và phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là \(2m,\; 7m\) và chiều cao \(10m\).
Thể tích hình hộp chữ nhật là:
\(V = 10.25.2 = 500 (m^3) \)
Thể tích lăng trụ đứng tam giác là:
\(V = S.h = \dfrac{1}{2}. 2.7.10 = 70\) \((m^3) \)
Vậy bể bơi có thể chứa số mét khối nước khi đầy ắp nước là:
\( 500 +70 = 570(m^3) \)
Bài 30 trang 114 SGK Toán lớp 8 tập 2
Câu hỏi:
Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.
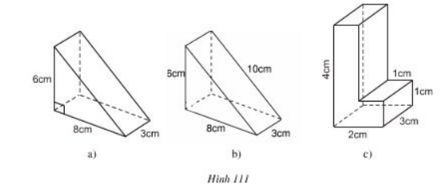
Lời giải:
+) Hình a là lăng trụ đứng có chiều cao là \(3cm\) và đáy là tam giác vuông có hai cạnh góc vuông là \(6cm,\; 8cm\).
Suy ra cạnh huyền là \(\sqrt{6^{2}+8^{2}} = \sqrt{36+64} = \sqrt{100} = 10\) \((cm)\).
Diện tích đáy là : \(S = \dfrac{1}{2}6 . 8 = 24(cm^2) \)
Thể tích lăng trụ là: \(V = S.h = 24.3 = 72(cm^3) \)
Diện tích xung quanh lăng trụ là:
\(S_{xq} =2p.h = (6+8+10).3 = 24.3 \)\(=72 \) \((cm^2)\)
Diện tích toàn phần lăng trụ là:
\(S_{tp} =S_{xq}+2. S_{đ} = 72 +2.24 =120\) \((cm^2)\)
+) Hình b là lăng trụ đứng tam giác có ba kích thước là \(6cm,\, 8cm, \,10cm\); chiều cao lăng trụ là \(3cm\).
Vì \(6^2 + 8^2 = 36 + 64 = 100 = 10^2 \) nên đáy lăng trụ là tam giác vuông có hai cạnh góc vuông là \(6cm,\, 8cm\). Do đó, bài toán này quay về bài toán ở hình a, ta thu được kết quả:
\(V= 72cm^3; \quad S_{xq} = 72 cm^2;\)\( \quad S_{tp} =120(cm^2)\).
+) Hình c là hình gồm hai lăng trụ đứng: Hình lăng trụ một là hình hộp chữ nhật có các kích thước \(4cm, \; 1cm,\; 3cm\) ; hình lăng trụ hai là hình hộp chữ nhật có các kích thước \(1cm,\;1cm, \; 3cm\).
Thể tích lăng trụ một là: \( V_1 = 4.1.3 =12 (cm^3)\)
Thể tích lăng trụ hai là: \( V_2 = 1.1.3 =3 (cm^3)\)
Thể tích lăng trụ đã cho là
\( V = V_1+ V_2 = 12 +3 =15 (cm^3)\)
Diện tích xung quanh của lăng trụ một là:
\( S_{xq1} = 2.(3+1).4 =32 (cm^2)\)
Diện tích một đáy của lăng trụ một là:
\( S_{đ1} = 3.1 =3 (cm^2) \)
Diện tích toàn phần của lăng trụ một là:
\( S_{tp1} =S_{xq1} +2. S_{đ1} = 32 +2.3 =38 \) \((cm^2)\)
Diện tích xung quanh của lăng trụ hai là:
\( S_{xq2} = 2.(1+3).1 =8 (cm^2)\)
Diện tích một đáy của lăng trụ hai là:
\( S_{đ2} = 3.1 =3 (cm^2) \)
Diện tích toàn phần của lăng trụ hai là:
\( S_{tp2} =S_{xq2} +2. S_{đ2} = 8 +2.3=14\) \( (cm^2)\)
Diện tích toàn phần của lăng trụ đã cho bằng tổng diện tích toàn phần của lăng trụ 1 và 2 trừ đi 2 phần diện tích chung là hình chữ nhật với các kích thước \(1cm,\; 3cm\). Do đó:
\( S_{tp} =S_{tp1} +S_{tp2} - 2. S_{hcn} \)
\(=38 + 14 - 2.3.1 =46 (cm^2)\)
Bài 31 trang 115 SGK Toán lớp 8 tập 2
Câu hỏi:
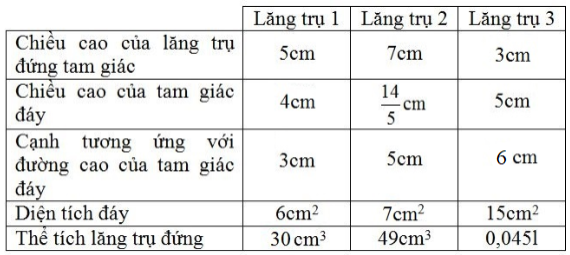
Điền số thích hợp vào các ô trống ở bảng sau:
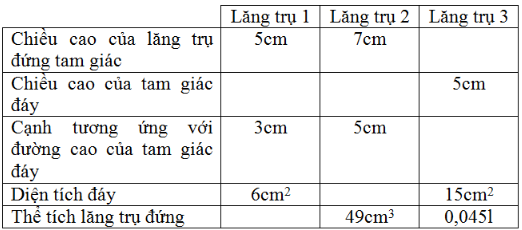
Lời giải:
Với \(V\) là thể tích của lăng trụ, \(S\) là diện tích đáy, \(h_1\) là chiều cao của lăng trụ đứng tam giác, \(h\) là chiều cao của tam giác đáy, \(a\) là cạnh tương ứng với đường cao của tam giác đáy.
+) Lăng trụ 1 : \(h_1=5cm, a=3cm, S=6cm^2\)
\(h = \dfrac{2S}{a} = \dfrac{2.6}{3} = 4(cm) \)
\(V = S.h_1 = 6.5 = 30(cm^3) \)
+) Lăng trụ 2: \(h_1=7cm, a=5cm, V=49cm^3\)
\(S = \dfrac{V}{h_{1}}= \dfrac{49}{7}= 7(cm^2) \)
\(h =\dfrac{2S}{a} = \dfrac{2.7}{5} = \dfrac{14}{5}(cm) \)
+) Lăng trụ 3: \(h=5cm, S=15cm^2, V=0,045l\)
Ta có \(0,045l = 0,045dm^3= 45(cm^3) \)
\(h_1=\dfrac{V}{S} = \dfrac{45}{15} = 3(cm) \)
\(a = \dfrac{2S}{h} = \dfrac{2.15}{5}= 6 (cm) \)
Điền vào bảng, ta được kết quả sau:
Bài 32 trang 115 SGK Toán lớp 8 tập 2
Câu hỏi:
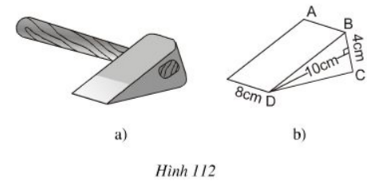
Hình 112b biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng, BDC là một tam giác cân.
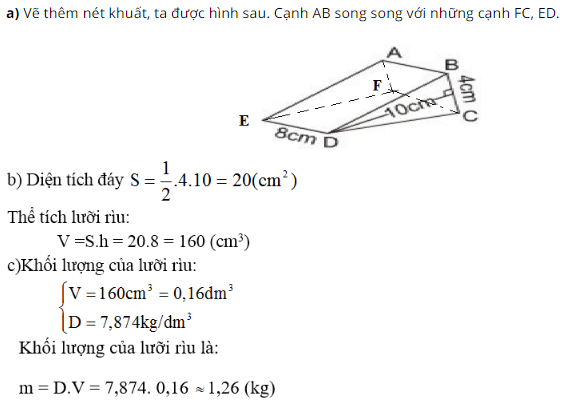
a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AB song song với những cạnh nào?
b) Tính thể tích lưỡi rìu.
c) Tính khối lượng của lưỡi rìu, biết khối lương riêng của sắt là 7,874 kg/dm3 (phần cán gỗ bên trong lưỡi rìu là không đáng kể).
Phương pháp:
a. Sử dụng định nghĩa và tính chất hình lăng trụ đứng.
b.- Thể tích \( V=S.h\), trong đó \( S\) là diện tích đáy, \(h \) là chiều cao.
c.- Khối lượng lưỡi rìu = khối lượng riêng \( \times \) thể tích lưỡi rìu.
Lời giải:
Bài 33 trang 115 SGK Toán lớp 8 tập 2
Câu hỏi:
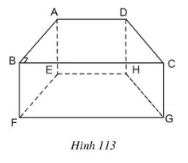
Hình 113 là một lăng trụ đứng, đáy là hình thang vuông.
Hãy kể tên:
a) Các cạnh song song với cạnh AD.
b) Cạnh song song với cạnh AB.
c) Các đường thẳng song song với mặt phẳng (EFGH).
d) Các đường thẳng song song với mặt phẳng (DCGH).
Phương pháp:
Dựa vào tính chất của hình lăng trụ đứng và giả thiết đề bài cho đáy là hình thang vuông.
Lời giải:
a) Các cạnh song song với cạnh AD là EH, BC, FG.
b) Các cạnh song song với cạnh AB là EF.
c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.
d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.
Bài 34 trang 116 SGK Toán lớp 8 tập 2
Câu hỏi:
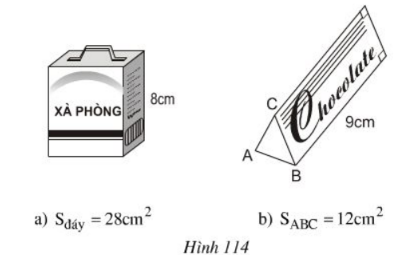
Tính thể tích của hộp xà phòng và hộp sô-cô-la trên hình 114, biết:
a) Diện tích đáy hộp xà phòng là 28cm2 (h.114a).
b) Diện tích tam giác ABC ở hình 114b là 12cm2.
Lời giải:
a.
Thể tích hộp xà phòng là:
\( V = S.h = 28.8 = 224 (cm^3 )\)
b.
Thể tích của hộp sô – cô – la là :
\(V = S. h = 12.9 = 108 (cm^3) \)
Bài 35 trang 116 SGK Toán lớp 8 tập 2
Câu hỏi:
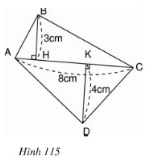
Đáy của một lăng trụ đứng là tứ giác, các kích thước cho theo hình 115. Biết chiều cao của lăng trụ là 10cm. Hãy tính thể tích của nó
Lời giải:
Diện tích đáy của lăng trụ là diện tích của tứ giác \(ABCD\).
Ta có :
\(S_{ABCD}= S_{ABC}+ S_{ADC}\).
\(= \dfrac{1}{2} .AC.BH + \dfrac{1}{2}.AC. DK \)
\(= \dfrac{1}{2} .8.3 + \dfrac{1}{2}. 8.4 = 12 + 16 = 28\,cm^2 \)
Thể tích của lăng trụ là :
\(V = S.h = 28.10 = 280 (cm^3) \)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 41, 42, 43, 44, 45, 46, 47 trang 132, 133 SGK Toán 8 tập 1 - Ôn tập chương 2 (28/06)
- Bài 37, 38, 39, 40 trang 130, 131 SGK Toán 8 tập 1 - Diện tích đa giác (28/06)
- Bài 32, 33, 34, 35, 36 trang 128, 129 SGK Toán 8 tập 1 - Diện tích hình thoi (28/06)
- Bài 26, 27, 28, 29, 30, 31 trang 125, 126 SGK Toán 8 tập 1 - Diện tích hình thang (28/06)
- Bài 19, 20, 21, 22, 23, 24, 25 trang 121 SGK Toán 8 tập 1 - Luyện tập (28/06)
- Ôn tập cuối năm
- Chương IV. Hình lăng trụ đứng. Hình chóp đều
- Chương III. Tam giác đồng dạng
- Chương IV. Bất phương trình bậc nhất một ẩn
- Chương III. Phương trình bậc nhất một ẩn
- GIẢI SGK TOÁN 8 TẬP 2
- Chương II: Đa giác. Diện tích đa giác
- Chương I. Tứ giác
- Chương II. Phân thức đại số
- Chương I. Phép nhân và phép chia các đa thức
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
