Bài 29, 30, 31 trang 83 SGK Toán 8 tập 1 - Dựng hình bằng thước và com-pa. Dựng hình thang
Bài 29, 30, 31 trang 83 SGK Toán 8 tập 1 - Dựng hình bằng thước và com-pa. Dựng hình thang. Bài Dựng (∆ABC) vuông tại (A), biết cạnh huyền (BC = 4,cm), góc nhọn.
Bài 29 trang 83 SGK Toán lớp 8 tập 1
Câu hỏi:
Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = 4\,cm\), góc nhọn \(\widehat{B}={65^0}\)
Phương pháp:
Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = a\,cm\), góc nhọn \(\widehat{B}={x^0}\)
Cách dựng:
- Dựng đoạn thẳng \(BC=a\,cm\)
- Dựng \(\widehat {CBx} = {x^o}\)
- Dựng \(CA\bot Bx\)
Lời giải:
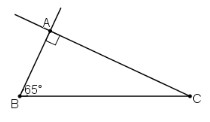
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
Bài 30 trang 83 SGK Toán 8 tập 1
Câu hỏi:
Dựng tam giác \(ABC\) vuông tại \(B\), biết cạnh huyền \(AC = 4\,cm\), cạnh góc vuông \(BC = 2\,cm.\)
Phương pháp:
Dựng tam giác \(ABC\) vuông tại \(B\), biết cạnh huyền \(AC = b\,cm\), cạnh góc vuông \(BC = a\,cm.\)
Cách dựng:
- Dựng \(\widehat {xBy} = {90^0}\). Trên tia \(Bx\) lấy điểm \(C\) sao cho \(BC = a\,cm.\)
- Dựng cung tròn \((C; b\,cm)\) và cung tròn này cắt tia \(By\) tại \(A.\)
- Nối \(A\) với \(C\) ta được \(∆ABC\) là tam giác cần dựng.
Lời giải:
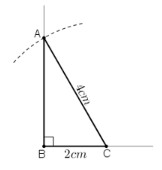
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Bài 31 trang 83 SGK Toán 8 tập 1
Câu hỏi:
Dựng hình thang \(ABCD\; (AB // CD)\), biết \(AB = AD = 2\,cm,\) \( AC = DC = 4\,cm.\)
Phương pháp:
Áp dụng phương pháp dựng tam giác, hình thang.
Lời giải:
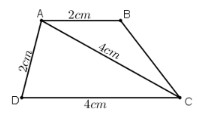
a) Phân tích :
Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.
Tam giác ADC dựng được vì biết ba cạnh của tam giác.
Điểm B phải thỏa mãn hai điều kiện :
+ B nằm trên tia Ax song song với CD
+ B cách A một đoạn 2cm.
b) Cách dựng:
+ Dựng tam giác ADC có AD = 2cm, AC = 4cm, CD = 4cm.
+ Dựng tia Ax song song với CD và nằm trên cùng một nửa mặt phẳng chứa điểm C bờ là đường thẳng AD.
+ Trên tia Ax lấy điểm B sao cho AB = 2cm.
Kẻ BC ta được hình thang ABCD cần dựng.
c) Chứng minh
Tứ giác ABCD là hình thang vì AB // CD.
Hình thang ABCD có AB = AD = 2cm, AC = BC = 4cm thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 41, 42, 43, 44, 45, 46, 47 trang 132, 133 SGK Toán 8 tập 1 - Ôn tập chương 2 (28/06)
- Bài 37, 38, 39, 40 trang 130, 131 SGK Toán 8 tập 1 - Diện tích đa giác (28/06)
- Bài 32, 33, 34, 35, 36 trang 128, 129 SGK Toán 8 tập 1 - Diện tích hình thoi (28/06)
- Bài 26, 27, 28, 29, 30, 31 trang 125, 126 SGK Toán 8 tập 1 - Diện tích hình thang (28/06)
- Bài 19, 20, 21, 22, 23, 24, 25 trang 121 SGK Toán 8 tập 1 - Luyện tập (28/06)
- Ôn tập cuối năm
- Chương IV. Hình lăng trụ đứng. Hình chóp đều
- Chương III. Tam giác đồng dạng
- Chương IV. Bất phương trình bậc nhất một ẩn
- Chương III. Phương trình bậc nhất một ẩn
- GIẢI SGK TOÁN 8 TẬP 2
- Chương II: Đa giác. Diện tích đa giác
- Chương I. Tứ giác
- Chương II. Phân thức đại số
- Chương I. Phép nhân và phép chia các đa thức
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
