Bài tập cuối chương 3 trang 40, 41, 42, 43, 44 SBT Toán 10 tập 1 Kết nối tri thức

A. TRẮC NGHIỆM

Bài 3.17 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(\widehat A = {15^ \circ },\,\,\widehat B = {45^ \circ }.\) Giá trị của \(\tan C\) bằng:

A. \( - \sqrt 3 .\)

B. \(\sqrt 3 .\)

C. \(\frac{1}{{\sqrt 3 }}.\)

D. \( - \frac{1}{{\sqrt 3 }}.\)

Lời giải:

Xét \(\Delta ABC\) có: \(\widehat C = {180^ \circ } - \widehat A - \widehat B = {180^ \circ } - {15^ \circ } - {45^ \circ } = {120^ \circ }\)

Ta có \(\tan C = \tan {120^ \circ } =  - \sqrt 3 .\)

Chọn A.

Bài 3.18 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^ \circ }.\) Tích hoành độ và tung độ của điểm \(M\) bằng

A. \(\frac{1}{{2\sqrt 2 }}.\)

B. \(\frac{1}{2}\)

C. \( - \frac{1}{2}\)

D. \( - \frac{1}{{2\sqrt 2 }}.\)

Lời giải:

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{x = \cos \widehat {xOM}}\\{y = \sin \widehat {xOM}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{x = \cos {{135}^ \circ } = \frac{{ - \sqrt 2 }}{2}}\\{y = \sin {{135}^ \circ } = \frac{{\sqrt 2 }}{2}}\end{array}} \right.} \right.\,\, \Rightarrow \,\,M\left( {\frac{{ - \sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\)

Tích hoành độ và tung độ điểm \(M\) là: \(\frac{{ - \sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{{ - 1}}{2}.\)

Chọn C.

Bài 3.19 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }.\) \(N\) là điểm đối xứng với \(M\) qua trục tung. Giá trị của \(\tan \widehat {xON}\) bằng:

A. \(\frac{1}{{\sqrt 3 }}.\)

B. \( - \frac{1}{{\sqrt 3 }}.\)

C. \(\sqrt 3 .\)

D. \( - \sqrt 3 .\)

Lời giải:

Ta có: \(\widehat {xON} = {180^ \circ } - {150^ \circ } = {30^ \circ }.\)

\( \Rightarrow \,\,\tan \widehat {xON} = \tan {30^ \circ } = \frac{{\sqrt 3 }}{3}.\)

Chọn A.

Bài 3.20 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho góc nhọn \(\alpha \) có \(\tan \alpha  = \frac{3}{4}.\) Giá trị của \(\sin \alpha .\cos \alpha \) bằng

A. \(\frac{4}{3}.\)

B. \(\frac{{12}}{{25}}.\)

C. \(\frac{{25}}{{12}}.\)

D. \(\frac{3}{4}.\)

Lời giải:

Ta có: \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\,\, \Rightarrow \,\,{\cos ^2}\alpha  = \frac{1}{{1 + {{\tan }^2}\alpha }} = \frac{1}{{1 + {{\left( {\frac{3}{4}} \right)}^2}}} = \frac{{16}}{{25}}\)

Ta có: \(\sin \alpha .\cos \alpha  = \tan \alpha .{\cos ^2}\alpha  = \frac{3}{4}.\frac{{16}}{{25}} = \frac{{12}}{{25}}.\)

Chọn B.

Bài 3.21 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho góc nhọn \(\alpha \,\,\left( {{0^ \circ } < \alpha  < {{180}^ \circ }} \right)\) thỏa mãn \(\sin \alpha  + \cos \alpha  = 1.\) Giá trị của \(\cot \alpha \) bằng:

A. \(0.\)

B. \(1.\)

C. \( - 1.\)

D. Không tồn tại

Lời giải:

Điều kiện \(\sin \alpha  \ne 0\)

Ta có: \(\sin \alpha  + \cos \alpha  = 1\)

\(\begin{array}{l} \Leftrightarrow \,\,{\left( {\sin \alpha  + \cos \alpha } \right)^2} = 1\\ \Leftrightarrow \,\,{\sin ^2}\alpha  + 2\sin \alpha .\cos \alpha  + {\cos ^2}\alpha  = 1\\ \Leftrightarrow \,\,2\sin \alpha .\cos \alpha  = 0\\ \Leftrightarrow \,\,\left[ {\begin{array}{*{20}{c}}{\sin \alpha  = 0}\\{\cos \alpha  = 0}\end{array}} \right.\,\, \Leftrightarrow \,\,\cos \alpha  = 0\end{array}\)

Ta có: \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = 0.\)

Chọn A.

Bài 3.22 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho góc \(\alpha \) thỏa mãn \(\sin \alpha  + \cos \alpha  = \sqrt 2 .\) Giá trị của \(\tan \alpha  + \cot \alpha \) là:

A. 1.

B. \( - 2\).

C. 0.

D. 2.

Lời giải:

Ta có: \(\sin \alpha  + \cos \alpha  = \sqrt 2 \)

\(\begin{array}{l} \Leftrightarrow {\left( {\sin \alpha  + \cos \alpha } \right)^2} = {\left( {\sqrt 2 } \right)^2} = 2\\ \Leftrightarrow {\sin ^2}\alpha  + 2\sin \alpha .\cos \alpha  + {\cos ^2}\alpha  = 2\\ \Leftrightarrow 1 + 2\sin \alpha .\cos \alpha  = 2\\ \Leftrightarrow 2\sin \alpha .\cos \alpha  = 1\\ \Leftrightarrow \sin \alpha .\cos \alpha  = \frac{1}{2}\end{array}\)

Ta có: \(\tan \alpha  + \cot \alpha \)

\(\begin{array}{l} = \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }}\\ = \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\frac{1}{2}}} = 2.\end{array}\)

Chọn D

Bài 3.23 trang 40 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diện tích của tam giác \(AOM\) bằng:

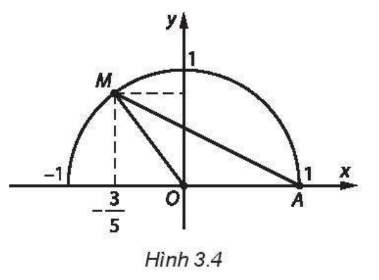
A. \(\frac{4}{5}.\)

B. \(\frac{2}{5}.\)

C. \(\frac{3}{5}.\)

D. \(\frac{3}{{10}}.\)

Lời giải:

Diện tích \(\Delta AOM\) là: \(S = \frac{1}{2}.\frac{3}{5}.OA = \frac{3}{{10}}.\)

Chọn D.

Bài 3.24 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }\)(H.3.5). \(N\) là điểm đối xứng với \(M\) qua trục tung. Diện tích của tam giác \(MAN\) bằng:

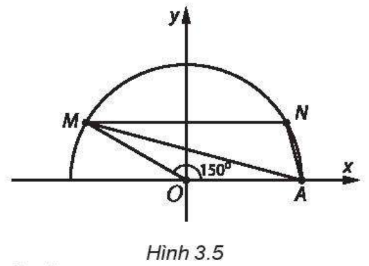
A. \(\frac{{\sqrt 3 }}{4}.\)

B. \(\frac{{\sqrt 3 }}{2}.\)

C. \(\sqrt 3 .\)

D. \(2\sqrt 3 .\)

Lời giải:

Ta có: \(\sin \widehat {xOM} = \sin {150^ \circ } = \frac{1}{2}\) và \(\cos \widehat {xOM} = \cos {150^ \circ } = \frac{{ - \sqrt 3 }}{2}.\)

Diện tích \(\Delta MAN\) là: \(S = \frac{1}{2}.\left| {2\cos \widehat {xOM}} \right|.\left| {\sin \widehat {xOM}} \right| = \frac{1}{2}.\left| {2.\frac{{ - \sqrt 3 }}{2}} \right|.\left| {\frac{1}{2}} \right| = \frac{{\sqrt 3 }}{4}.\)

Chọn A.

Bài 3.25 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho \(\cos \alpha  = \frac{1}{4}.\) Giá trị của \(P = \frac{{\tan \alpha  + 2\cot \alpha }}{{2\tan \alpha  + 3\cot \alpha }}\) là:

A. \( - \frac{{17}}{{33}}.\)

B. \(\frac{{17}}{{33}}.\)

C. \(\frac{1}{2}.\)

D. \(\frac{{16}}{{33}}.\)

Lời giải:

Ta có: \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\,\, \Rightarrow {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }} - 1 = 15.\)

Ta có: \(P = \frac{{\tan \alpha  + 2\cot \alpha }}{{2\tan \alpha  + 3\cot \alpha }} = \frac{{\frac{{\tan \alpha }}{{\cot \alpha }} + 2}}{{\frac{{2\tan \alpha }}{{\cot \alpha }} + 3}} = \frac{{{{\tan }^2}\alpha  + 2}}{{2{{\tan }^2}\alpha  + 3}} = \frac{{15 + 2}}{{2.15 + 3}} = \frac{{17}}{{33}}.\)

Chọn B.

Bài 3.26 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(a = 2,\,\,b = 3,\,\,c = 4.\) Bán kính đường tròn ngoại tiếp của tam giác \(ABC\) là:

A. \(R = \frac{{\sqrt {15} }}{2}.\)

B. \(R = \frac{7}{{\sqrt {15} }}.\)

C. \(R = \frac{{\sqrt {15} }}{6}.\)

D. \(R = \frac{8}{{\sqrt {15} }}.\)

Lời giải:

Nửa chu vi \(\Delta ABC\) là: \(p = \frac{{a + b + c}}{2} = \frac{{2 + 3 + 4}}{2} = \frac{9}{2}.\)

Diện tích \(\Delta ABC\) là:

\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \sqrt {\frac{9}{2}\left( {\frac{9}{2} - 2} \right)\left( {\frac{9}{2} - 3} \right)\left( {\frac{9}{2} - 4} \right)}  = \frac{{3\sqrt {15} }}{4}\)

Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là: \(R = \frac{{abc}}{{4S}} = \frac{{2.3.4}}{{4.\frac{{3\sqrt {15} }}{4}}} = \frac{8}{{\sqrt {15} }}.\)

Chọn D.

Bài 3.27 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(a = 4,\,\,b = 5,\,\,c = 6.\) Độ dài đường cao \({h_b}\) bằng:

A. \(\frac{{3\sqrt 7 }}{2}.\)

B. \(\frac{3}{{2\sqrt 7 }}.\)

C. \(\frac{{3\sqrt 7 }}{4}.\)

D. \(\frac{3}{{4\sqrt 7 }}.\)

Lời giải:

Nửa chu vi \(\Delta ABC\) là: \(p = \frac{{a + b + c}}{2} = \frac{{4 + 5 + 6}}{2} = \frac{{15}}{2}.\)

Diện tích \(\Delta ABC\) là:

\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \sqrt {\frac{{15}}{2}\left( {\frac{{15}}{2} - 4} \right)\left( {\frac{{15}}{2} - 5} \right)\left( {\frac{{15}}{2} - 6} \right)}  = \frac{{15\sqrt 7 }}{4}.\)

Độ dài đường cao hạ từ đỉnh B là: \({h_b} = \frac{{2S}}{b} = \frac{{2.\frac{{15\sqrt 7 }}{4}}}{5} = \frac{{3\sqrt 7 }}{2}.\)

Chọn A.

Bài 3.28 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(a = 20,\,\,b = 16\) và \({m_a} = 10.\) Diện tích của tam giác bằng:

A. \(92.\)

B. \(100.\)

C. \(96.\)

D. \(88.\)

Lời giải:

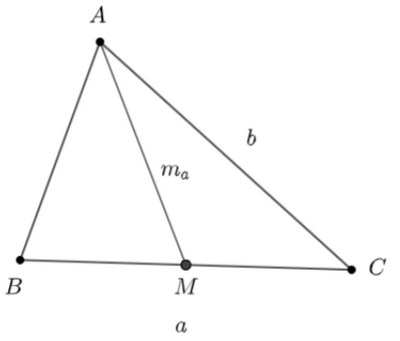
Nửa chu vi \(\Delta AMC\) là: \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2} = \frac{{10 + 10 + 16}}{2} = 18.\)

Diện tích \(\Delta AMC\) là:

\({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)}  = \sqrt {18\left( {18 - 10} \right)\left( {18 - 10} \right)\left( {18 - 16} \right)}  = 48.\)

Diện tích \(\Delta ABC\) là:  \(S = 2{S_{\Delta AMC}} = 2.48 = 96\)

Chọn C.

Bài 3.29 trang 41 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(a = 14,\,\,b = 9\) và \({m_a} = 8.\) Độ dài đường cao \({h_a}\) bằng:

A. \(\frac{{24\sqrt 5 }}{7}.\)

B. \(\frac{{12\sqrt 5 }}{7}.\)

C. \(12\sqrt 5 .\)

D. \(24\sqrt 5 .\)

Lời giải:

Nửa chu vi \(\Delta AMC\) là: \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2} = \frac{{7 + 8 + 9}}{2} = 12.\)

Diện tích \(\Delta AMC\) là:

\({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)}  = \sqrt {12\left( {12 - 7} \right)\left( {12 - 8} \right)\left( {12 - 9} \right)}  = 12\sqrt 5 .\)

Độ dài đường cao hạ từ đỉnh A là:

\({h_a} = \frac{{4{S_{\Delta AMC}}}}{a} = \frac{{4.12\sqrt 5 }}{{14}} = \frac{{24\sqrt 5 }}{7}.\)

Chọn A.

Bài 3.30 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(\widehat A = {45^ \circ },\,\,c = 6,\,\,\widehat B = {75^ \circ }.\)

Độ dài đường cao \({h_b}\) bằng:

A. \(3\sqrt 2 .\)

B. \(\frac{3}{{\sqrt 2 }}.\)

C. \(6\sqrt 2 .\)

D. \(2\sqrt 3 .\)

Lời giải:

Ta có: \(\widehat A + \widehat B + \widehat C = {180^ \circ }\,\, \Rightarrow \,\,\widehat C = {180^ \circ } - \widehat A - \widehat B = {60^ \circ }\)

Áp dụng định lý sin trong \(\Delta ABC\) ta có:

\(\begin{array}{l}\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\\ \Rightarrow \,\,b = \frac{{c.\sin B}}{{\sin C}} = \frac{{6.\sin {{75}^ \circ }}}{{\sin {{45}^ \circ }}} = 3 + 3\sqrt 3 \,\,\left( {dvdd} \right)\end{array}\)

Diện tích \(\Delta ABC\) là:

\({S_{\Delta ABC}} = \frac{1}{2}bc.\sin A = \frac{1}{2}.\left( {3 + 3\sqrt 3 } \right).6.\sin {45^ \circ } = \frac{{9\sqrt 6  + 9\sqrt 2 }}{2}\,\,\left( {dvdt} \right)\)

Ta có: \({S_{\Delta ABC}} = \frac{1}{2}{h_b}.b\,\, \Rightarrow \,\,{h_b} = \frac{{2{S_{\Delta ABC}}}}{b} \approx \frac{{2.\frac{{9\sqrt 6  + 9\sqrt 2 }}{2}}}{{3 + 3\sqrt 3 }} = 3\sqrt 2 \,\,\left( {dvdd} \right)\)

Chọn A.

Bài 3.31 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(\widehat A = {45^ \circ },\,\,c = 6,\,\,\widehat B = {75^ \circ }.\) Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng:

A. \(8\sqrt 3 .\)

B. \(2\sqrt 3 .\)

C. \(6\sqrt 3 .\)

D. \(4\sqrt 3 .\)

Lời giải:

Xét \(\Delta ABC\) có: \(\widehat C = {180^ \circ } - \widehat A - \widehat B = {180^ \circ } - {45^ \circ } - {75^ \circ } = {60^ \circ }\)

Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là:

Áp dụng định lý sin, ta có:

\(\frac{c}{{\sin C}} = 2R\,\, \Leftrightarrow \,\,\frac{6}{{\sin {{60}^ \circ }}} = 2R\,\, \Leftrightarrow \,\,R = 2\sqrt 3 .\)

Chọn B.

Bài 3.32 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có diện tích \(S = 2R{}^2.\sin B.\sin C,\) với \(R\) là độ dài bán kính đường tròn ngoại tiếp tam giác. Số đo góc \(A\) bằng:

A. \({60^ \circ }\)

B. \({90^ \circ }\)

C. \({30^ \circ }\)

D. \({75^ \circ }\)

Lời giải:

Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = 2R.\sin A}\\{b = 2R.\sin B}\\{c = 2R.\sin C}\end{array}} \right.\\\end{array}\)

Diện tích \(\Delta ABC\) là:

\(S = \frac{{abc}}{{4R}} = \frac{{2R\sin A.2R\sin B.2R\sin C}}{{4R}} = 2{R^2}\sin A.\sin B.\sin C\)

mặt khác \(S = 2R{}^2.\sin B.\sin C\)

nên \(\sin A = 1\,\, \Rightarrow \,\,\widehat A = {90^ \circ }\)

Chọn B.

Bài 3.33 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(AB = \sqrt 5 ,\,\,AC = \sqrt 2 ,\,\,\widehat C = {45^ \circ }.\) Độ dài cạnh \(BC\) bằng:

A. \(3.\)

B. \(2.\)

C. \(\sqrt 3 .\)

D. \(\sqrt 2 .\)

Lời giải:

Độ dài cạnh \(BC\) là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2AC.BC}}\,\, \Leftrightarrow \,\,\cos {45^ \circ } = \frac{{2 + B{C^2} - 5}}{{2\sqrt 2 .BC}} = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \,\,B{C^2} - 2BC - 3 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{BC = 3}\\{BC =  - 1}\end{array}} \right.\end{array}\)

Vì \(BC > 0\) nên \(BC = 3.\)

Chọn A.

Bài 3.34 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(\widehat C = {60^ \circ },\,\,AC = 2,\,\,AB = \sqrt 7 .\) Diện tích của tam giác \(ABC\) bằng:

A. \(\frac{{\sqrt 3 }}{2}.\)

B. \(3\sqrt 3 .\)

C. \(\frac{{3\sqrt 3 }}{2}.\)

D. \(\sqrt 3 .\)

Lời giải:

Áp dụng định lý sin, ta có:

\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\,\, \Leftrightarrow \,\,\frac{2}{{\sin B}} = \frac{{\sqrt 7 }}{{\sin {{60}^ \circ }}}\,\, \Leftrightarrow \,\,\sin B = \frac{{\sqrt {21} }}{7}\,\, \Leftrightarrow \,\,\widehat B \approx {41^ \circ }\)

Ta có: \(\widehat A = {180^ \circ } - \widehat B - \widehat C = {180^ \circ } - {41^ \circ } - {60^ \circ } = {79^ \circ }\)

Diện tích \(\Delta ABC\) là:

\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.\sqrt 7 .2.\sin {79^ \circ } \approx \frac{{3\sqrt 3 }}{2}\)

Chọn C.

Bài 3.35 trang 42 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Tam giác \(ABC\) có \(\widehat A = {60^ \circ },\,\,AB = 3,\,\,BC = 3\sqrt 3 .\) Độ dài bán kính đường tròn nội tiếp của tam giác \(ABC\) là:

A. \(\frac{{3\left( {\sqrt 3  - 1} \right)}}{2}.\)

B. \(\frac{{3\left( {\sqrt 3  + 1} \right)}}{2}.\)

C. \(\frac{{\sqrt 3  - 1}}{2}.\)

D. \(\sqrt 3  - 1.\)

Lời giải:

Độ dài đoạn thẳng \(AC\) là:

\(\begin{array}{l}\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \Leftrightarrow \frac{1}{2} = \frac{{9 + A{C^2} - 27}}{{6AC}}\\ \Leftrightarrow 2\left( {A{C^2} - 18} \right) = 6AC\\ \Leftrightarrow 2A{C^2} - 6AC - 36 = 0\\ \Leftrightarrow AC = 6.\end{array}\)

Nửa chu vi \(\Delta ABC\) là: \(p = \frac{{AB + AC + BC}}{2} = \frac{{3 + 6 + 3\sqrt 3 }}{2} = \frac{{9 + 3\sqrt 3 }}{2} = \frac{{3\sqrt 3 \left( {\sqrt 3  + 1} \right)}}{2}\)

Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.3.6\sin {60^ \circ } = \frac{{9\sqrt 3 }}{2}.\)

Bán kính đường tròn nội tiếp \(\Delta ABC\) là:

\(r = \frac{S}{p} = \frac{{9\sqrt 3 }}{2}:\frac{{3\sqrt 3 \left( {\sqrt 3  + 1} \right)}}{2} = \frac{3}{{\sqrt 3  + 1}} = \frac{{3\left( {\sqrt 3  - 1} \right)}}{2}\)

Chọn A.

Bài 3.36 trang 43 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Một ca nô xuất phát từ cảng A, chạy theo hướng đông với tốc độ 60 km/h. Cùng lúc đó, một tàu các xuất phát từ A, chạy theo hướng \(N{30^ \circ }E\) với vận tốc 50 km/h. Sau 2 giờ, hai tàu cách nhau bao nhiêu ki lô mét?

A. 110 km

B. 112 km

C. 111,4 km

D. 110,5 km

Lời giải:

Ta có: \(\widehat {BAC} = {90^ \circ } - {30^ \circ } = {60^ \circ }.\)

Quãng đường \(AB\) là: \(AB = 60.2 = 120\,\,km.\)

Quãng đường \(AC\) là: \(AC = 50.2 = 100\,\,km\)

Độ dài quãng đường \(BC\) là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\\ \Rightarrow \,\,B{C^2} = 14400 + 10000 - 2.120.100.\cos {60^ \circ }\\ \Rightarrow \,\,B{C^2} = 12400\\ \Rightarrow \,\,BC = \sqrt {12400}  \approx 111,4\,\,km\end{array}\)

Chọn C.

Bài 3.37 trang 43 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng là \({60^ \circ }\) và \({30^ \circ },\) so với phương nằm ngang (H.3.6). Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là:

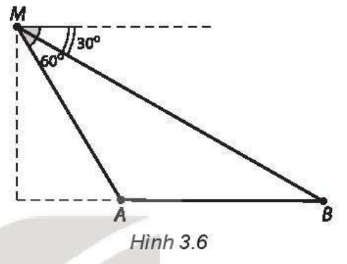
A. \(8m.\)

B. \(7m.\)

C. \(6m.\)

D. \(9m.\)

Lời giải:

Ta có: \(\widehat {AMB} = {60^ \circ } - {30^ \circ } = {30^ \circ }.\)

Ta có: \(\widehat {CMA} = {90^ \circ } - {60^ \circ } = {30^ \circ }.\)

Ta có: \(\widehat {CMB} = {30^ \circ } + {30^ \circ } = {60^ \circ }.\)

Xét \(\Delta CMB\) vuông tại \(C\) có: \(\widehat B = {90^ \circ } - \widehat {CMB} = {90^ \circ } - {60^ \circ } = {30^ \circ }\)

Xét \(\Delta CMA\) vuông tại \(C\) có: \(MA = \frac{{MC}}{{\cos \widehat {CMA}}} = \frac{6}{{\cos {{30}^ \circ }}} = 4\sqrt 3 \,\,m.\)

Xét \(\Delta ABM\) có \(\widehat {AMB} = \widehat B = {30^ \circ }\)

\( \Rightarrow \,\,\Delta ABM\) cân tại \(A\)

\( \Rightarrow \,\,AN = AB = 4\sqrt 3  \approx 7\,\,m\)

Chọn B.

B. TỰ LUẬN

Bài 3.38 trang 43 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho góc tù \(\alpha \) có \(\sin \alpha  = \frac{1}{3}.\)

a) Tính \(cos\alpha ,\,\,\tan \alpha ,\,\,\cot \alpha .\)

b) Tính giá trị của các biểu thức:

\(\) \(\begin{array}{l}A = \sin \alpha .\cot \left( {{{180}^ \circ } - \alpha } \right) + \cos \left( {{{180}^ \circ } - \alpha } \right).\cot \left( {{{90}^ \circ } - \alpha } \right).\\B = \frac{{3\left( {\sin \alpha  + \sqrt 2 .\cos \alpha } \right) - 2}}{{\sin \alpha  - \sqrt 2 .\cos \alpha }}.\end{array}\)

Lời giải:

a)  Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\,\, \Rightarrow \,\,{\cos ^2}\alpha  = 1 - {\sin ^2}\alpha  = \frac{8}{9}\,\, \Rightarrow \,\,\cos \alpha  = \frac{{ - 2\sqrt 2 }}{3}.\)

Ta có: \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \sqrt 2 }}{4}\) và \(\cot \alpha  =  - 2\sqrt 2 \)

b) \(A = \sin \alpha .\cot \left( {{{180}^ \circ } - \alpha } \right) + \cos \left( {{{180}^ \circ } - \alpha } \right).\cot \left( {{{90}^ \circ } - \alpha } \right)\)

\(\begin{array}{l}A = \sin \alpha .\left( { - \cot \alpha } \right) + \left( { - \cos \alpha } \right).\tan \alpha \\A =  - \cos \alpha  + \left( { - \sin \alpha } \right) = \frac{{2\sqrt 2 }}{3} - \frac{1}{3} = \frac{{2\sqrt 2  - 1}}{3}.\end{array}\)

\(\begin{array}{l}B = \frac{{3\left( {\sin \alpha  + \sqrt 2 .\cos \alpha } \right) - 2}}{{\sin \alpha  - \sqrt 2 .\cos \alpha }}\\B = \frac{{3\left( {\frac{1}{3} - \sqrt 2 .\frac{{2\sqrt 2 }}{3}} \right) - 2}}{{\frac{1}{3} + \sqrt 2 .\frac{{2\sqrt 2 }}{3}}} = \frac{{ - 5}}{{\frac{5}{3}}} =  - 3.\end{array}\)

Bài 3.39 trang 43 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho \(\sin {15^ \circ } = \frac{{\sqrt 6  - \sqrt 2 }}{4}.\)

a) Tính \(\sin {75^ \circ },\,\,\cos {105^ \circ },\,\,\tan {165^ \circ }.\)

b) Tính giá trị của biểu thức

\(A = \sin {75^ \circ }.\cos {165^ \circ } + \cos {105^ \circ }.\sin {165^ \circ }.\)

Lời giải:

Ta có: \({\sin ^2}{15^ \circ } + {\cos ^2}{15^ \circ } = 1\)

\(\begin{array}{l} \Rightarrow \,\,{\cos ^2}{15^ \circ } = 1 - {\sin ^2}{15^ \circ } = \frac{{2 + \sqrt 3 }}{4}\\ \Rightarrow \,\,\cos {15^ \circ } = \sqrt {\frac{{2 + \sqrt 3 }}{4}}  = \sqrt {\frac{{8 + 4\sqrt 3 }}{{16}}}  = \sqrt {\frac{{{{\left( {\sqrt 6 } \right)}^2} + 2.\sqrt 6 .\sqrt 2  + {{\left( {\sqrt 2 } \right)}^2}}}{{16}}} \\ \Rightarrow \,\,\cos {15^ \circ } = \sqrt {\frac{{{{\left( {\sqrt 6  + \sqrt 2 } \right)}^2}}}{{16}}}  = \frac{{\sqrt 6  + \sqrt 2 }}{4}.\end{array}\)

Ta có: \(\tan {15^ \circ } = \frac{{\sin {{15}^ \circ }}}{{\cos {{15}^ \circ }}} = \frac{{\sqrt 6  - \sqrt 2 }}{4}:\frac{{\sqrt 6  + \sqrt 2 }}{4} = 2 - \sqrt 3 \)

a) \(\sin {75^ \circ } = \sin \left( {{{90}^ \circ } - {{15}^ \circ }} \right) = \cos {15^ \circ } = \frac{{\sqrt 6  + \sqrt 2 }}{4}.\)

\(\cos {105^ \circ } = \cos \left( {{{180}^ \circ } - {{75}^ \circ }} \right) =  - \cos {75^ \circ } =  - \cos \left( {{{90}^ \circ } - {{15}^ \circ }} \right) =  - \sin {15^ \circ } = \frac{{\sqrt 2  - \sqrt 6 }}{4}.\)

\(\tan {165^ \circ } = \tan \left( {{{180}^ \circ } - {{15}^ \circ }} \right) =  - \tan {15^ \circ } = \sqrt 3  - 2.\)

b) \(A = \sin {75^ \circ }.\cos {165^ \circ } + \cos {105^ \circ }.\sin {165^ \circ }.\)

Ta có: \(\cos {165^ \circ } = \cos \left( {{{180}^ \circ } - {{15}^ \circ }} \right) =  - \cos {15^ \circ } =  - \frac{{\sqrt 2  + \sqrt 6 }}{4}.\)

Ta có: \(\sin {165^ \circ } = \tan {165^ \circ }.\cos {165^ \circ } =  - \left( {\sqrt 3  - 2} \right).\frac{{\sqrt 2  + \sqrt 6 }}{4} = \frac{{\sqrt 6  - \sqrt 2 }}{4}.\)

\(\begin{array}{l}A = \sin {75^ \circ }.\cos {165^ \circ } + \cos {105^ \circ }.\sin {165^ \circ }\\A = \frac{{\sqrt 6  + \sqrt 2 }}{4}.\left( { - \frac{{\sqrt 2  + \sqrt 6 }}{4}} \right) + \frac{{\sqrt 2  - \sqrt 6 }}{4}.\frac{{\sqrt 6  - \sqrt 2 }}{4}\\A = \frac{{ - 4\sqrt 3  - 8}}{{16}} + \frac{{ - 8 + 16\sqrt 3 }}{{16}} = \frac{{ - 16}}{{16}} =  - 1.\end{array}\)

Bài 3.40 trang 43 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(AB = 1,\,\,BC = 2,\,\,\widehat {ABC} = {60^ \circ }.\) Tính độ dài cạnh và số đo các góc còn lại của tam giác

Lời giải:

Độ dài cạnh \(AC\) là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\\ \Rightarrow \,\,A{C^2} = 1 + 4 - 2.1.2.\cos {60^ \circ } = 3\\ \Rightarrow \,\,AC = \sqrt 3 .\end{array}\)

Áp dụng định lý sin, ta có:

\(\left\{ {\begin{array}{*{20}{c}}{\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}}\\{\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\sin A = \frac{{BC.\sin B}}{{AC}} = \frac{{2.\sin {{60}^ \circ }}}{{\sqrt 3 }} = 1}\\{\sin C = \frac{{AB.\sin B}}{{AC}} = \frac{{1.\sin {{60}^ \circ }}}{{\sqrt 3 }} = \frac{1}{2}}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\widehat A = {{90}^ \circ }}\\{\widehat C = {{30}^ \circ }}\end{array}} \right.} \right.} \right.\)

Bài 3.41 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(c = 1,\,\,a = 2,\,\,\widehat B = {120^ \circ }.\)

a) Tính \(b,\,\,\widehat A,\,\,\widehat C.\)

b) Tính diện tích của tam giác

c) Tính độ dài đường cao kẻ từ \(B\) của tam giác

Lời giải:

a) Áp dụng định lý cosin, ta có:

\(\begin{array}{l}{b^2} = {a^2} + {c^2} - 2ac.\cos B\\ \Rightarrow \,\,{b^2} = 4 + 1 - 2.2.1.\cos {120^ \circ } = 7\\ \Rightarrow \,\,b = \sqrt 7 .\end{array}\)

Áp dụng định lý sin, ta có:

\(\left\{ {\begin{array}{*{20}{c}}{\frac{a}{{\sin A}} = \frac{b}{{\sin B}}}\\{\frac{c}{{\sin C}} = \frac{b}{{\sin B}}}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\sin A = \frac{{a.\sin B}}{b} = \frac{{2.\sin {{120}^ \circ }}}{{\sqrt 7 }} = \frac{{\sqrt {21} }}{7}}\\{\sin C = \frac{{c.\sin B}}{b} = \frac{{1.\sin {{120}^ \circ }}}{{\sqrt 7 }} = \frac{{\sqrt {21} }}{{14}}}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\widehat A \approx {{41}^ \circ }}\\{\widehat C \approx {{19}^ \circ }}\end{array}} \right.} \right.} \right.\)

b) Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}ac.\sin B = \frac{1}{2}.2.1.\sin {120^ \circ } = \frac{{\sqrt 3 }}{2}\)

c) Độ dài đường cao kẻ từ \(B\) của \(\Delta ABC\) là: \({h_b} = \frac{{2S}}{b} = \frac{{\sqrt {21} }}{7}.\)

Bài 3.42 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(a = 3,\,\,b = 5,\,\,c = 7.\)

a) Tính các góc của tam giác, làm tròn đến độ.

b) Tính bán kính đường tròn nội tiếp và đường tròn ngoại tiếp của tam giác.

Lời giải:

a) Áp dụng định lý cosin, ta có:

\(\left\{ {\begin{array}{*{20}{c}}{\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}\\{\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}}\\{\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\cos A = \frac{{25 + 49 - 9}}{{2.5.7}} = \frac{{13}}{{14}}}\\{\cos B = \frac{{9 + 49 - 25}}{{2.3.7}} = \frac{{11}}{{14}}}\\{\cos C = \frac{{9 + 25 - 49}}{{2.3.5}} = \frac{{ - 1}}{2}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\widehat A \approx {{22}^ \circ }}\\{\widehat B \approx {{38}^ \circ }}\\{\widehat C = {{120}^ \circ }}\end{array}} \right.} \right.} \right.\)

b) Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là:

\(R = \frac{c}{{2\sin C}} = \frac{7}{{2.\sin {{120}^ \circ }}} = \frac{{7\sqrt 3 }}{3}.\)

Nửa chu vi \(\Delta ABC\) là: \(p = \frac{{a + b + c}}{2} = \frac{{3 + 5 + 7}}{2} = \frac{{15}}{2}.\)

Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}ab\sin C = \frac{1}{2}.3.5.\sin {120^ \circ } = \frac{{15\sqrt 3 }}{4}.\)

Bán kính đường tròn nội tiếp \(\Delta ABC\) là: \(r = \frac{S}{p} = \frac{{15\sqrt 3 }}{4}:\frac{{15}}{2} = \frac{{\sqrt 3 }}{2}.\)

Bài 3.43 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(\widehat B = {45^ \circ },\,\,\widehat C = {15^ \circ },\,\,b = \sqrt 2 .\) Tính \(a,\,\,{h_a}.\)

Lời giải:

Xét \(\Delta ABC\) có: \(\widehat A = {180^ \circ } - \widehat B - \widehat C = {180^ \circ } - {45^ \circ } - {15^ \circ } = {120^ \circ }.\)

Áp dụng định lý sin, ta có:

\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\,\, \Leftrightarrow \,\,\frac{a}{{\sin {{120}^ \circ }}} = \frac{{\sqrt 2 }}{{\sin {{45}^ \circ }}}\,\, \Leftrightarrow a = \frac{{\sqrt 2 .\sin {{120}^ \circ }}}{{\sin {{45}^ \circ }}} = \sqrt 3 .\)

Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}ab\sin C = \frac{1}{2}.\sqrt 3 .\sqrt 2 .\sin {15^ \circ } = \frac{{3 - \sqrt 3 }}{4}.\)

Độ dài đường cao hạ từ đỉnh A là: \({h_a} = \frac{{2S}}{a} = \frac{{2.\frac{{3 - \sqrt 3 }}{4}}}{{\sqrt 3 }} = \frac{{\sqrt 3  - 1}}{2}.\)

Bài 3.44 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(c = 5,\,\,a = 8,\,\,\widehat B = {60^ \circ }.\)

a) Tính \(b\) và các góc của \(A,C\) (số đo các góc làm tròn đến hàng đơn vị, theo đơn vị độ).

b) Tính độ dài đường cao kẻ từ \(B.\)

c) Tính độ dài trung tuyến kể từ \(A.\)

Lời giải:

a) Áp dụng định lý cosin, ta có:

\(\begin{array}{l}{b^2} = {a^2} + {c^2} - 2ac.\cos B\\ \Rightarrow \,\,{b^2} = 64 + 25 - 2.8.5.\cos {60^ \circ } = 49\\ \Rightarrow \,\,b = 7.\end{array}\)

Áp dụng định lý cosin, ta có:

\(\left\{ {\begin{array}{*{20}{c}}{\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}\\{\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}}\end{array}} \right.\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\cos A = \frac{{49 + 25 - 64}}{{2.7.5}} = \frac{1}{7}}\\{\cos C = \frac{{64 + 49 - 25}}{{2.8.7}} = \frac{{11}}{{14}}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\widehat A \approx {{82}^ \circ }}\\{\widehat C \approx {{38}^ \circ }}\end{array}} \right.} \right.\)

b) Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}ac.\sin B = \frac{1}{2}.8.5.\sin {60^ \circ } = 10\sqrt 3 .\)

Độ dài đường cao kẻ từ \(B\) là: \({h_b} = \frac{{2S}}{b} = \frac{{2.10\sqrt 3 }}{7} = \frac{{20\sqrt 3 }}{7}.\)

c) Độ dài đường trung tuyến kẻ từ \(A\) là:

\(\begin{array}{l}m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} = \frac{{49 + 25}}{2} - \frac{{64}}{4} = 21\\ \Rightarrow \,\,{m_a} = \sqrt {21} .\end{array}\)

Bài 3.45 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(\widehat B = {15^ \circ },\,\,\widehat C = {30^ \circ },\,\,c = 2.\)

a) Tính số đo góc \(A\) và độ dài các cạnh \(a,b.\)

b) Tính diện tích và bán kính đường tròn ngoại tiếp của tam giác.

c) Lấy điểm \(D\) thuộc cạnh \(AB\) sao cho \(\widehat {BCD} = \widehat {DCA}\) (tức \(CD\) là tia phân giác của \(\widehat {BCA}\)). Tính độ dài \(CD.\)

Lời giải:

a) Xét \(\widehat A = {180^ \circ } - \widehat B - \widehat C = {180^ \circ } - {15^ \circ } - {30^ \circ } = {135^ \circ }.\)

Áp dụng định lý sin, ta có:

\(\left\{ {\begin{array}{*{20}{c}}{\frac{a}{{\sin A}} = \frac{c}{{\sin C}}}\\{\frac{b}{{\sin B}} = \frac{c}{{\sin C}}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{\frac{a}{{\sin {{135}^ \circ }}} = \frac{2}{{\sin {{30}^ \circ }}}}\\{\frac{b}{{\sin {{15}^ \circ }}} = \frac{2}{{\sin {{30}^ \circ }}}}\end{array}\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{{2\sin {{135}^ \circ }}}{{\sin {{30}^ \circ }}} = 2\sqrt 2 }\\{b = \frac{{2\sin {{15}^ \circ }}}{{\sin {{30}^ \circ }}} = \sqrt 6  - \sqrt 2 }\end{array}} \right.} \right.} \right.\)

b) Diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}ac.\sin B = \frac{1}{2}.2\sqrt 2 .2.\sin {15^ \circ } = \sqrt 3  - 1\)

Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là:

Áp dụng định lý sin, ta có:

\(\frac{c}{{\sin C}} = 2R\,\, \Leftrightarrow \,\,\frac{2}{{\sin {{30}^ \circ }}} = 2R\,\, \Leftrightarrow \,\,R = 2.\)

c) Ta có: \(CD\) là tia phân giác của \(\widehat {ACB}\)

\( \Rightarrow \) \(\widehat {ACD} = \widehat {BCD} = \frac{1}{2}\widehat {ACB} = {15^ \circ }\)

Gọi \(I\) là trung điểm của \(BC\) và \(IB = IC = \sqrt 2 .\)

Xét \(\Delta BCD\) có \(\widehat {DCB} = \widehat B = {15^ \circ }\)

\( \Rightarrow \) \(\Delta BCD\) cân tại \(D.\)

Mặt khác \(I\) là trung điểm của \(BC.\)

\( \Rightarrow \) \(DI \bot BC\)

Xét \(\Delta CDI\) vuông tại \(I\) có: \(CD = \frac{{IC}}{{\sin \widehat {DCB}}} = \frac{{\sqrt 2 }}{{\sin {{15}^ \circ }}} = 2 + 2\sqrt 3 .\)

Bài 3.46 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên biển, một tàu cá xuất phát từ cảng A, chạy về phương đông 15 km tới B, rồi chuyển sang hướng \(E{30^ \circ }S\) chạy tiếp 20 km nữa tới đảo C.

a) Tính khoảng cách từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị ki lô mét).

b) Xác định hướng từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị độ).

Lời giải:

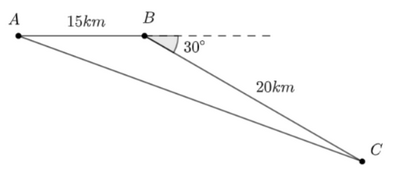
a) Ta có: \(\widehat {ABC} = {180^ \circ } - {30^ \circ } = {150^ \circ }.\)

Khoảng cách từ A đến C là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2AB.BC.\cos \widehat {ABC}\\ \Rightarrow \,\,A{C^2} = 225 + 400 - 2.15.20.\cos {150^ \circ }\\ \Rightarrow \,\,A{C^2} \approx 1144.6\\ \Rightarrow \,\,AC \approx 33.8\end{array}\)

b) Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{BC}}{{\sin \widehat A}}\,\, \Leftrightarrow \,\,\frac{{33.8}}{{\sin {{150}^ \circ }}} = \frac{{20}}{{\sin \widehat A}}\\ \Leftrightarrow \,\,\sin \widehat A = \frac{{20.\sin {{150}^ \circ }}}{{33.8}} \approx 0.296\\\,\, \Leftrightarrow \widehat A = {17^ \circ }.\end{array}\)

Vậy từ A tới C là hướng \(E{17^ \circ }S.\)

Bài 3.47 trang 44 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trên sườn đồi, với độ dốc \(12\% \) (độ dốc của sườn đồi được tính bằng tang của một góc tạo bởi sườn đồi với phương nằm ngang) có một cây cao mọc thẳng đứng. Ở phía chân đồi, cách gốc cây 30m, người ta nhìn ngọn cây dưới một góc \({45^ \circ }\) so với phương nằm ngang. Tính chiều cao của cây đó (làm tròn đến hàng đơn vị, theo đơn vị mét).

Lời giải:

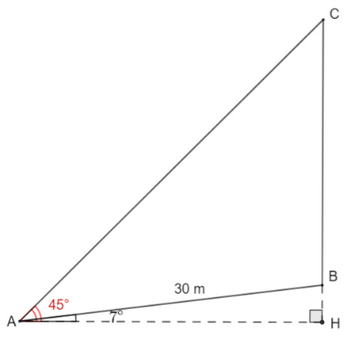
Do sườn đồi có độ dốc \(12\% \) nên sườn đồi tạo với phương nằm ngang một góc \(\tan HAB = 12\% \,\, \Rightarrow \,\,\widehat {HAB} = {\tan ^{ - 1}}\left( {12\% } \right) \approx {7^ \circ }\)

Ta có: \(\widehat {BAC} = \widehat {HAC} - \widehat {HAB} \approx {45^ \circ } - {7^ \circ } \approx {38^ \circ }\) và \(\widehat {BCA} = {45^ \circ }\)

Áp dụng định lý sin trong \(\Delta ABC,\) ta có:

\(\begin{array}{l}\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\\ \Rightarrow \,\,BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}}\\ \Rightarrow \,\,BC = \frac{{30.\sin {{38}^ \circ }}}{{\sin {{45}^ \circ }}} \approx 26\,\,\left( m \right)\end{array}\)

Sachbaitap.com