Bài 4.54, 4.55, 4.56, 4.57, 4.58, 4.59 trang 69 SBT Toán 10 tập 1 Kết nối tri thức

A. TRẮC NGHIỆM

Bài 4.54 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(A(2; - 1),\,\,B( - 1;5)\) và \(C(3m;2m - 1).\) Tất cả các giá trị của tham số m sao cho \(AB \bot OC\) là:

A. \(m =  - 2\)

B. \(m = 2\)

C. \(m =  \pm 2\)

D. \(m = 3\)

Lời giải:

Ta có: \(\overrightarrow {AB}  = ( - 3;6)\) và \(\overrightarrow {OC}  = (3m;2m - 1)\)

Để \(AB \bot OC\) \( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {OC}  = 0\)

\( \Leftrightarrow \) \( - 3.3m + 6\left( {2m - 1} \right) = 0\)

\( \Leftrightarrow \) \( - 9m + 12m - 6 = 0\)

\( \Leftrightarrow \) \(3m = 6\) \( \Leftrightarrow \) \(m = 2\)

Vậy \(m = 2\) là giá trị cần tìm

Chọn B.

Bài 4.55 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 1,\,\,AC = 2.\) Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(2BM = MC,\,\,CN = 2NA,\,\,AP = 2PB.\) Giá trị của tích vô hướng \(\overrightarrow {AM} .\overrightarrow {NP} \) bằng

A. \(\frac{2}{3}\)

B. \( - \frac{1}{2}\)

C. \(0\)

D. \(1\)

Lời giải:

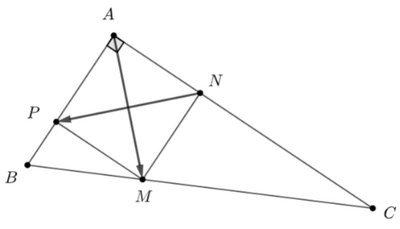
Ta có: \(\frac{{CN}}{{CA}} = \frac{{CM}}{{CM}} = \frac{2}{3}\)

\( \Rightarrow \) \(MN\)//\(AB\) hay \(MN\)//\(AP\)       (1)

Ta có: \(\frac{{BP}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{3}\)

\( \Rightarrow \) \(MP\)//\(AC\) hay \(MP\)//\(AN\)       (2)

Ta có: \(AP = \frac{2}{3}AB = \frac{2}{3}.1 = \frac{2}{3}\) và \(AN = \frac{1}{3}AC = \frac{2}{3}\)

Từ (1) và (2) \( \Rightarrow \) tứ giác \(APMN\) là hình bình hành

Mặt khác \(\widehat {PAN} = {90^ \circ }\) và \(AP = AN = \frac{2}{3}\)

\( \Rightarrow \) tứ giác \(APMN\) là hình vuông

\( \Rightarrow \) \(AM \bot PN\) \( \Rightarrow \overrightarrow {AM} .\overrightarrow {NP}  = 0\)

Chọn C.

Bài 4.56 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) đều các cạnh có độ dài bằng 1. Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(BM = 2MC,\,\,CN = 2NA\) và \(AM \bot NP.\) Tỉ số của \(\frac{{AP}}{{AB}}\) bằng

A. \(\frac{5}{{12}}\)

B. \(\frac{7}{{12}}\)

C. \(\frac{5}{7}\)

D. \(\frac{7}{5}\)

Lời giải:

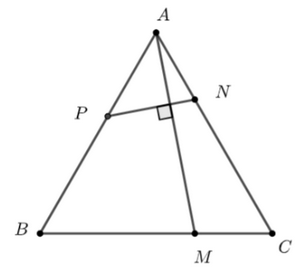
Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)

Ta có: \(\overrightarrow {PN}  = \overrightarrow {PA}  + \overrightarrow {AN}  = \frac{1}{3}\overrightarrow {AC}  - x\overrightarrow {AB} \)

Ta có: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM}  = \overrightarrow {AB}  + \frac{2}{3}\overrightarrow {BC}  = \overrightarrow {AB}  + \frac{2}{3}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB}  + \frac{2}{3}\overrightarrow {AC} \)

Ta có: \(AM \bot PN\) \( \Rightarrow \) \(\overrightarrow {AM} .\overrightarrow {PN}  = 0\)

\( \Leftrightarrow \) \(\left( {\frac{1}{3}\overrightarrow {AB}  + \frac{2}{3}\overrightarrow {AC} } \right).\left( {\frac{1}{3}\overrightarrow {AC}  - x\overrightarrow {AB} } \right) = 0\)

\( \Leftrightarrow \) \(\frac{1}{9}\overrightarrow {AB} .\overrightarrow {AC}  - \frac{x}{3}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{{2x}}{3}\overrightarrow {AC} .\overrightarrow {AB}  = 0\)

\( \Leftrightarrow \) \(\frac{1}{9}.\frac{1}{2} - \frac{x}{3} + \frac{2}{9} - \frac{{2x}}{3}.\frac{1}{2} = 0\)

\( \Leftrightarrow \) \(\frac{1}{{18}} - \frac{x}{3} + \frac{2}{9} - \frac{x}{3} = 0\)

\( \Leftrightarrow \) \(1 - 6x + 4 - 6x = 0\)

\( \Leftrightarrow \) \(12x = 5\) \( \Leftrightarrow \) \(x = \frac{5}{{12}}\)

Vậy \(\frac{{AP}}{{AB}} = \frac{5}{{12}}\)

Chọn A.

Bài 4.57 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) đều có độ dài cạnh bằng \(3a\). Lấy điểm \(M\) thuộc cạnh \(BC\) sao cho \(MB = 2MC.\) Tích vô hướng của hai vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {MC} \) bằng

A. \(\frac{{{a^2}}}{2}\)

B. \( - \frac{{{a^2}}}{2}\)

C. \({a^2}\)

D. \( - {a^2}\)

Lời giải:

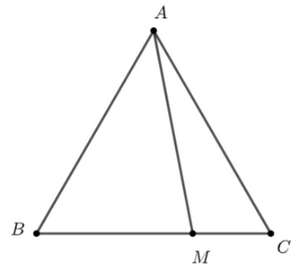
Ta có: \(\overrightarrow {MA}  = \overrightarrow {MB}  + \overrightarrow {BA}  =  - \overrightarrow {AB}  - \frac{2}{3}\overrightarrow {BC}  =  - \frac{1}{3}\overrightarrow {AB}  - \frac{2}{3}\overrightarrow {AC} \)

\(\overrightarrow {MC}  = \frac{1}{3}\overrightarrow {CB}  = \frac{1}{3}\left( {\overrightarrow {AB}  - \overrightarrow {AC} } \right) = \frac{1}{3}\overrightarrow {AB}  - \frac{1}{3}\overrightarrow {AC} \)

Ta có: \(\overrightarrow {MA} .\overrightarrow {MC}  = \left( { - \frac{1}{3}\overrightarrow {AB}  - \frac{2}{3}\overrightarrow {AC} } \right)\left( {\frac{1}{3}\overrightarrow {AB}  - \frac{1}{3}\overrightarrow {AC} } \right)\)

\(\begin{array}{l} =  - \frac{1}{9}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{1}{9}\overrightarrow {AB} .\overrightarrow {AC} \\ =  - \frac{1}{9}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{1}{9}.AB.AC.\cos \widehat {BAC}\\ =  - \frac{1}{9}.9{a^2} + \frac{2}{9}.9{a^2} - \frac{1}{9}.9{a^2}.\cos {60^ \circ }\\ =  - {a^2} + 2{a^2} - {a^2}.\frac{1}{2} = \frac{{{a^2}}}{2}\end{array}\)

Chọn A.

Bài 4.58 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC.\) Tập hợp các điểm \(M\) thỏa mãn \(\left| {\overrightarrow {MC}  - \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC}  - \overrightarrow {AC} } \right|\) là:

A. Đường tròn tâm \(A\) bán kính \(BC\)

B. Đường thẳng đi qua \(A\) và song song với \(BC\)

C. Đường tròn đường kính \(BC\)

D. Đường thẳng đi qua \(A\) và vuông góc với \(BC\)

Lời giải:

Ta có: \(\left| {\overrightarrow {MC}  - \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC}  - \overrightarrow {AC} } \right|\)

\( \Leftrightarrow \) \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {MC}  + \overrightarrow {CA} } \right|\)

\( \Leftrightarrow \) \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {MA} } \right|\)

\( \Rightarrow \) Tập hợp điểm \(M\) là đường tròn tâm \(A\) bán kính \(BC\)

Chọn A.

B. TỰ LUẬN

Bài 4.59 trang 69 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho hình bình hành ABCD tâm O. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi I, J lần lượt là giao điểm của BD với AM, CN. Xét các vectơ khác vecto 0 có đầu mút lấy từ các điểm A, B, C, D, M, N, I, J, O.

a) Hãy chỉ ra những vectơ bằng vectơ \(\overrightarrow {AB} ;\) những vectơ cùng hướng với \(\overrightarrow {AB} .\)

b) Chứng minh rằng \(BI = IJ = JD.\)

Lời giải:

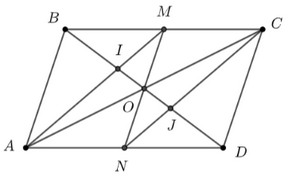
a) Các vectơ bằng vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} ,\,\,\overrightarrow {NM} ,\,\,\overrightarrow {CD} \)

Các vectơ cùng hướng với \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} ,\,\,\overrightarrow {NO} ,\,\,\overrightarrow {OM} ,\,\,\overrightarrow {CD} \)

b) Ta có: \(I\) là trọng tâm của \(\Delta ABC\)

\( \Rightarrow \) \(\overrightarrow {BI}  = \frac{2}{3}\overrightarrow {BO}  = \frac{2}{3}.\frac{1}{2}\overrightarrow {BD}  = \frac{1}{3}\overrightarrow {BD} \)      (1)

Ta có: \(J\) là trọng tâm của \(\Delta ACD\)

\( \Rightarrow \) \(\overrightarrow {JD}  = \frac{2}{3}\overrightarrow {OD}  = \frac{2}{3}.\frac{1}{2}\overrightarrow {BD}  = \frac{1}{3}\overrightarrow {BD} \)      (2)

Ta có: \(\overrightarrow {BD}  = \overrightarrow {BI}  + \overrightarrow {IJ}  + \overrightarrow {JD} \)

\( \Rightarrow \) \(\overrightarrow {IJ}  = \overrightarrow {BD}  - \overrightarrow {BI}  - \overrightarrow {JD}  = \overrightarrow {BD}  - \frac{1}{3}\overrightarrow {BD}  - \frac{1}{3}\overrightarrow {BD}  = \frac{1}{3}\overrightarrow {BD} \)      (3)

Từ (1), (2) và (3) \( \Rightarrow \) \(\overrightarrow {BI}  = \overrightarrow {IJ}  = \overrightarrow {JD} \) \( \Rightarrow \) \(BI = IJ = JD\)

Sachbaitap.com