Bài 47, 48, 49, 50 trang 22, 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
Giải bài 47, 48, 49 trang 22, bài 50 trang 23 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử. Bài 49: Tính nhanh: (37,5 . 6,5 - 7,5 . 3,4 - 6,6 . 7,5 + 3,5 . 37,5) ({45^2} + {40^2} - {15^2} + 80.45).
- Bài 51, 52, 53, 54, 55, 56, 57, 58 trang 24, 25 SGK Toán 8 tập 1 - Phân tích đa thức...
- Bài 59, 60, 61, 62 trang 26, 27 SGK Toán 8 tập 1 - Chia đơn thức cho đơn thức
- Bài 63, 64, 65, 66 trang 28, 29 SGK Toán 8 tập 1 - Chia đa thức cho đơn thức
- Bài 67, 68, 69, 70, 71, 72, 73, 74 trang 31, 32 SGK Toán 8 tập 1 - Chia đa thức một...
Bài 47 trang 22 SGK Toán lớp 8 tập 1
Câu hỏi:
Phân tích cá đa thức sau thành nhân tử:
\({x^2} - xy + x - y\);
\(xz + yz - 5(x + y)\);
\(3{x^2} - 3xy - 5x + 5y\).
Phương pháp:
Áp dụng phương pháp nhóm các hạng tử để xuất hiện nhân tử chung.
Cách 1: Nhóm hai hạng tử đầu tiên với nhau và hai hạng tử cuối với nhau
Cách 2: Nhóm hạng tử thứ 1 và thứ 3, nhóm hạng tử thứ 2 và thứ 4
Lời giải:
a) Cách 1: Nhóm hai hạng tử thứ 1 và thứ 2, hạng tử thứ 3 và thứ 4
x2 – xy + x – y
= (x2 – xy) + (x – y) (Nhóm thứ nhất có nhân tử chung là x)
= x(x – y) + (x – y) (Xuất hiện nhân tử chung x – y)
= (x + 1)(x – y)
Cách 2: Nhóm hạng tử thứ 1 và thứ 3 ; hạng tử thứ 2 và thứ 4
x2 – xy + x – y
= (x2 + x) – (xy + y)
(nhóm thứ nhất có nhân tử chung là x ; nhóm thứ hai có nhân tử chung là y)
= x.(x + 1) – y.(x + 1) (Xuất hiện nhân tử chung x + 1)
= (x – y)(x + 1)
b) xz + yz – 5(x + y)
= (xz + yz) – 5(x + y) (Nhóm thứ nhất có nhân tử chung là z ; nhóm thứ hai có nhân tử chung là 5)
= z(x + y) – 5(x + y) (Xuất hiện nhân tử chung là x + y)
= (z – 5)(x + y)
c) Cách 1: Nhóm hai hạng tử đầu tiên với nhau và hai hạng tử cuối với nhau:
3x2 – 3xy – 5x + 5y
= (3x2 – 3xy) – (5x – 5y)
(Nhóm thứ nhất có nhân tử chung là 3x ; nhóm thứ hai có nhân tử chung là 5)
= 3x(x – y) – 5(x – y) (Xuất hiện nhân tử chung là (x – y))
= (x – y)(3x – 5)
Cách 2: Nhóm hạng tử thứ 1 với hạng tử thứ 3; hạng tử thứ 2 với hạng tử thứ 4:
3x2 – 3xy – 5x + 5y
= (3x2 – 5x) – (3xy – 5y)
(Nhóm thứ nhất có nhân tử chung là x, nhóm thứ hai có nhân tử chung là y)
= x.(3x – 5) – y.(3x – 5)
(Xuất hiện nhân tử chung 3x – 5)
= (x – y).(3x – 5).
Bài 48 trang 22 SGK Toán lớp 8 tập 1
Câu hỏi:
Phân tích các đa thức sau thành nhân tử:
\({x^2} + 4x - {y^2} + 4\);
\(3{x^2} + 6xy + 3{y^2} - 3{z^2}\);
\({x^2} - 2xy + {y^2} - {z^2} + 2zt - {t^2}\)
Phương pháp:
- Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử và phương pháp dùng hằng đẳng thức.
- Áp dụng các hằng đẳng thức:
\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
\({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)
Lời giải:
a) Nhận thấy x2 + 4x + 4 là hằng đẳng thức nên ta nhóm với nhau.
x2 + 4x – y2 + 4
= (x2 + 4x + 4) – y2
= (x + 2)2 – y2 (Xuất hiện hằng đẳng thức (3))
= (x + 2 – y)(x + 2 + y)
b) 3x2 + 6xy + 3y2 – 3z2
= 3.(x2 + 2xy + y2 – z2)
(Nhận thấy xuất hiện x2 + 2xy + y2 là hằng đẳng thức nên ta nhóm với nhau)
= 3[(x2 + 2xy + y2) – z2]
= 3[(x + y)2 – z2]
= 3(x + y – z)(x + y + z)
c) x2 – 2xy + y2 – z2 + 2zt – t2
(Nhận thấy x2 – 2xy + y2 và z2 – 2zt + t2 là các hằng đẳng thức)
= (x2 – 2xy + y2) – (z2 – 2zt + t2)
= (x – y)2 – (z – t)2 (xuất hiện hằng đẳng thức (3))
= [(x – y) – (z – t)][(x – y) + (z – t)]
= (x – y – z + t)(x – y + z –t)
Bài 49 trang 22 SGK Toán lớp 8 tập 1
Câu hỏi:
Tính nhanh:
\(37,5 . 6,5 - 7,5 . 3,4 - 6,6 . 7,5 + 3,5 . 37,5\)
\({45^2} + {40^2} - {15^2} + 80.45\).
Phương pháp:
câu 1: Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử để xuất hiện nhân tử chung.
Nhóm hạng tử thứ 1 và thứ 4, nhóm hạng tử thứ 2 và thứ 3.
câu 2:
Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm nhóm và phương pháp dùng hằng đẳng thức.
\(\eqalign{
& {\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2} \cr
& {A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right) \cr} \)
Lời giải:
a) 37,5.6,5 – 7,5.3,4 – 6,6.7.5 + 3,5.37,5
(Hạng tử đầu tiên và cuối cùng đều có nhân tử 37,5; hai hạng tử giữa đều có nhân tử 7,5)
= (37,5.6,5 + 3,5.37,5) – (7,5.3,4 + 6,6.7,5)
= 37,5(6,5 + 3,5) – 7,5(3,4 + 6,6)
= 37,5.10 – 7,5.10
= 375 – 75 = 300
b) 452 + 402 – 152 + 80.45
= 452 + 80.45 + 402 – 152
= 452 + 2.45.40 + 402 – 152
= (45 + 40)2 – 152
= 852 – 152
= (85 – 15)(85 + 15)
= 70.100 = 7000
Bài 50 trang 23 SGK Toán lớp 8 tập 1
Câu hỏi:
Tìm \(x\), biết:
\(x(x - 2) + x - 2 = 0\);
\(5x(x - 3) - x + 3 = 0\).
Phương pháp:
Áp dụng phương pháp nhóm để phân tích vế trái thành tích \(A.B = 0\), khi đó hoặc \(A= 0\) hoặc \(B = 0\) (\(A, B\) là các đa thức).
Chú ý: có nhân tử chung \(x-3\)
Lời giải:
a) x(x – 2) + x – 2 = 0
(Xuất hiện nhân tử chung x – 2)
⇔ (x – 2)(x + 1) = 0
⇔ x – 2 = 0 hoặc x + 1 = 0
+ x – 2 = 0 ⇔ x = 2
+ x + 1 = 0 ⇔ x = –1
Vậy x = – 1 hoặc x = 2.
b) 5x(x – 3) – x + 3 = 0
⇔">⇔⇔ 5x(x – 3) – (x – 3) = 0
(Xuất hiện nhân tử chung x – 3)
⇔">⇔⇔ (x – 3)(5x – 1) = 0
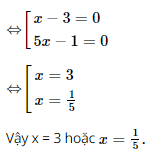
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 41, 42, 43, 44, 45, 46, 47 trang 132, 133 SGK Toán 8 tập 1 - Ôn tập chương 2 (28/06)
- Bài 37, 38, 39, 40 trang 130, 131 SGK Toán 8 tập 1 - Diện tích đa giác (28/06)
- Bài 32, 33, 34, 35, 36 trang 128, 129 SGK Toán 8 tập 1 - Diện tích hình thoi (28/06)
- Bài 26, 27, 28, 29, 30, 31 trang 125, 126 SGK Toán 8 tập 1 - Diện tích hình thang (28/06)
- Bài 19, 20, 21, 22, 23, 24, 25 trang 121 SGK Toán 8 tập 1 - Luyện tập (28/06)
- Ôn tập cuối năm
- Chương IV. Hình lăng trụ đứng. Hình chóp đều
- Chương III. Tam giác đồng dạng
- Chương IV. Bất phương trình bậc nhất một ẩn
- Chương III. Phương trình bậc nhất một ẩn
- GIẢI SGK TOÁN 8 TẬP 2
- Chương II: Đa giác. Diện tích đa giác
- Chương I. Tứ giác
- Chương II. Phân thức đại số
- Chương I. Phép nhân và phép chia các đa thức
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
