Bài 61, 62, 63, 64 trang 91, 92 SGK Toán 9 tập 2 - Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 61 trang 91 SGK Toán lớp 9 tập 2

Câu hỏi:

a) Vẽ đường tròn tâm \(O\), bán kính \(2cm\).

b) Vẽ hình vuông nội tiếp đường tròn \((O)\) ở câu a)

c) Tính bán kính \(r\) của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn \((O;r)\).

Lời giải:

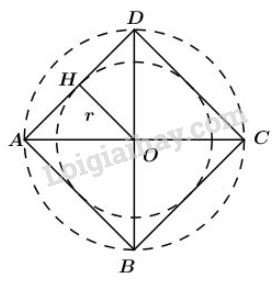
a) Chọn điểm \(O\) làm tâm, mở compa có độ dài \(2cm\) vẽ đường tròn tâm \(O\), bán kính \(2cm\): \((O; 2cm).\)

Vẽ bằng eke và thước thẳng. 

b) Vẽ đường kính \(AC\) và \(BD\) vuông góc với nhau. Nối \(A\) với \(B\), \(B\) với \(C\), \(C\) với \(D\), \(D\) với \(A\) ta được tứ giác \(ABCD\) là hình vuông nội tiếp đường tròn \((O;2cm)\)

c) Kẻ \(OH \bot AD.\)

Khi đó ta có \(OH\) là bán kính \(r\) của đường tròn nội tiếp hình vuông \(ABCD.\) Vì \(AB = BC = CD = DA\) ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau và cùng bằng OH ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây) 

Ta có: \(\Delta OAD\) là tam giác vuông cân tại \(O\) lại có \(OH\) là đường cao \(\Rightarrow \, H\) là trung điểm của \(AD \Rightarrow OH=AH=HD.\)

\( \Rightarrow r = OH = AH.\)

 Áp dụng định lý Pi-ta-go cho tam giác vuông \(OHD\) ta có:

\(OH^2+AH^2=OA^2\) \(\Leftrightarrow {r^2} + {r^2}  = {2^2} \Rightarrow 2{r^2} = 4 \Rightarrow r = \sqrt 2 (cm).\)

Vẽ đường tròn \((O;\sqrt2cm)\). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

Bài 62 trang 91 SGK Toán lớp 9 tập 2

Câu hỏi:

a) Vẽ tam giác \(ABC\) cạnh \(a = 3cm\).

b) Vẽ đường tròn \((O;R)\) ngoại tiếp tam giác đều \(ABC\). Tính \(R\).

c) Vẽ đường tròn \((O;r)\) nội tiếp tam giác đều \(ABC\). Tính \(r\).

d) Vẽ tiếp tam giác đều \(IJK\) ngoại tiếp đường tròn \((O;R)\).

Lời giải:

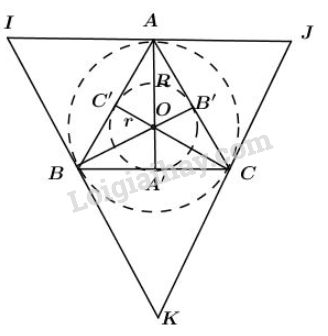
a) Vẽ tam giác đều \(ABC\) có cạnh bằng \(3cm\) (dùng thước có chia khoảng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) Gọi \(A';B';C'\) lần lượt là trung điểm của \(BC;AC;AB.\)

Tâm \(O\) của đường tròn ngoại tiếp tam giác đều \(ABC\) là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác \(AA';BB';CC'\) của tam giác đều \(ABC\)).

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính \(R=OA = OB = OC\) ta được đường tròn ngoại tiếp tam giác ABC.

Tính \(AA'\):

Xét tam giác \(AA'C\) vuông tại \(A'\) có \(AC=3;A'C=\dfrac{3}{2}\), theo định lý Pytago ta có \(AC^2=AA'^2+A'C^2\)\(\Rightarrow AA'^2=3^2-\dfrac {3^2}{4}=\dfrac {9}{4} \Rightarrow AA'=\dfrac {3\sqrt {3}}{2}\)

Theo cách dựng ta có O cũng là trọng tâm tam giác ABC nên \(OA=\dfrac{2}3AA'\) 

Ta có bán kính đường tròn ngoại tiếp tam giác ABC là   \(R= OA =\) \(\dfrac{2}{3}\)\(AA'\) = \(\dfrac{2}{3}\). \(\dfrac{3\sqrt{3}}{2}\) = \(\sqrt3 (cm)\).

c) Do tam giác ABC là tam giác đều các trung điểm A’; B’; C’ của các cạnh BC; CA; AB đồng thời là chân đường phân giác hạ từ A, B, C đến BC, AC, AB.

Đường tròn nội tiếp \((O;r)\) tiếp xúc ba cạnh của tam giác đều \(ABC\) tại các trung điểm \(A', B', C'\) của các cạnh.

Hay đường tròn (O; r) là đường tròn tâm O; bán kính \(r=OA’ = OB’ = OC’.\)

Ta có: \(r = OA' \)\(=\dfrac{1}{3}\)\( AA'\) \(=\dfrac{1}{3}.\dfrac{3\sqrt{3}}{2}\) \(=\dfrac{\sqrt{3}}{2}(cm).\)

d) Vẽ các tiếp tuyến với đường tròn \((O;R)\) tại \(A,B,C\). Ba tiếp tuyến này cắt nhau tại \(I, J, K\). Ta có \(∆IJK\) là tam giác đều ngoại tiếp \((O;R)\).  

Bài 63 trang 92 SGK Toán lớp 9 tập 2

Câu hỏi:

Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn \((O;R)\) rồi tính cạnh của các hình đó theo \(R\).

Phương pháp:

+) Sử dụng compa và thước kẻ có chia độ dài để vẽ hình.

+) Sử dụng định lý Pi-ta-go để tính R.

Lời giải:

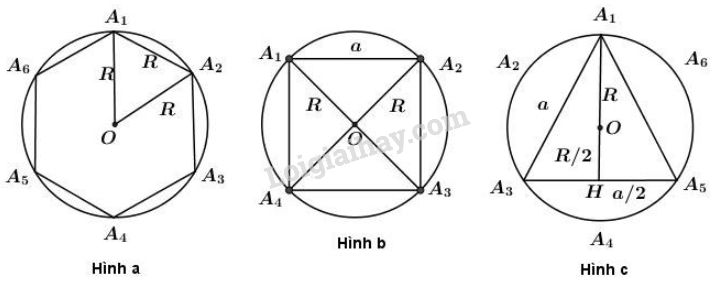
+) Hình a. 

Cách vẽ: vẽ đường tròn \((O;R)\). Trên đường tròn ta đặt liên tiếp các cung \(\overparen{{A_1}{A_2}}\),  \(\overparen{{A_2}{A_3}}\),...,\(\overparen{{A_6}{A_1}}\) mà dây căng cung có độ dài bằng \(R\). Nối \({A_1}\) với \({A_2}\), \({A_2}\) với \({A_3}\),…, \({A_6}\) với \({A_1}\) ta được hình lục giác đều \({A_1}\)\({A_2}\)\({A_3}\)\({A_4}\)\({A_5}\)\({A_6}\) nội tiếp đường tròn

Tính bán kính:

Gọi \({a_i}\)  là cạnh của đa giác đều có \(i\) cạnh.

\({a_6}= R\) (vì \(O{A_1}{A_2}\) là tam giác đều)

+) Hình b.

Cách vẽ:

+ Vẽ đường kính \(A_1A_3\) của đường tròn tâm O.

+ Vẽ đường kính \(A_2A_4 ⊥A_1A_3\)

Tứ giác \(A_1A_2A_3A_4\) có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.

Nối \(A_1\) với \(A_2;A_2\) với \(A_3;A_3\) với \(A_4;A_4\) với \(A_1\) ta được hình vuông \(A_1A_2A_3A_4\) nội tiếp đường tròn (O). 

Tính bán kính:

Gọi độ dài cạnh của hình vuông là \(a.\)

Vì hai đường chéo của hình vuông vuông góc với nhau nên xét tam giác vuông \(O{A_1}{A_2}\) có

\({a^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow a = R\sqrt 2 \)

+) Hình c: 

Cách vẽ như câu a) hình a. 

Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác \({A_1}{A_3}{A_5}\)  như trên hình c.

Tính bán kính: 

Gọi độ dài cạnh của tam giác đều  là \(a.\) 

\({A_1}H\) \(=A_1O+OH= R+\dfrac{R}{2}\) =  \(\dfrac{3R}{2}\)

\({A_3}H\) \(= \dfrac{AA'}{2}=\dfrac{a}{2}\)  

\({A_1}\)\({A_3}=a\)

Trong tam giác vuông \({A_1}H{A_3}\) ta có: \({A_1}{H^2} = {A_1}{A_3}^2 - {A_3}{H^2}\).

Từ đó \(\dfrac{9R^{2}}{4}\) = \(a^2\) - \(\dfrac{a^{2}}{4}\). 

\(\Rightarrow{a^2} = 3{R^2} \Rightarrow a = R\sqrt 3 \)

Bài 64 trang 92 SGK Toán lớp 9 tập 2

Câu hỏi:

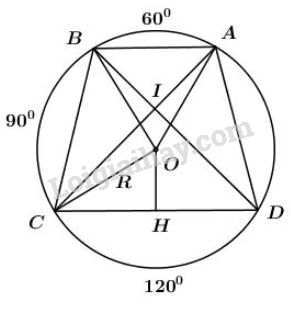
Trên đường tròn bán kính \(R\) lần lượt đặt theo cùng một chiều, kể từ điểm \(A\), ba cung \(\overparen{AB}\), \(\overparen{BC}\), \(\overparen{CD}\) sao cho: \(sđ\overparen{AB}\)=\(60^0\), \(sđ\overparen{BC}\)=\(90^0\), \(sđ\overparen{CD}\)=\(120^0\)

a) Tứ giác \(ABCD\) là hình gì?

b) Chứng minh hai đường chéo của tứ giác \(ABCD\) vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác \(ABCD\) theo \(R\).

Lời giải:

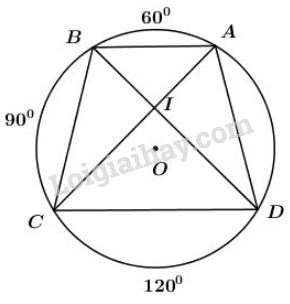
a) Xét đường tròn \((O)\) ta có:

\(\displaystyle \widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}\) (góc nội tiếp chắn \(\overparen{BCD}\))     (1)

\(\displaystyle \widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}\) ( góc nội tiếp chắn \(\overparen{ABC}\) )          (2)

Từ (1) và (2) có:

\(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}\) (3)

Mà hai góc này ở vị trí trong cùng phía 

Nên \(AB // CD\). Do đó tứ giác \(ABCD\) là hình thang, mà hình thang nội tiếp đường tròn là hình thang cân. 

Vậy \(ABCD\) là hình thang cân suy ra (\(BC = AD\) và \(sđ\overparen{BC}\)=\(sđ\overparen{AD}\)=\(90^0\))

b) Giả sử hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(I\).

\(\widehat {CI{\rm{D}}}\) là góc có đỉnh nằm trong đường tròn, nên:

\(\displaystyle \widehat {CI{\rm{D}}}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{CD}}{2}\)\(=\displaystyle {{{{60}^0} + {{120}^0}} \over 2} = {90^0}\)

Vậy \(AC \bot BD.\) 

c) Vì \(sđ\overparen{AB}= 60^0\) nên \(\widehat {AOB} = {60^0}\) (góc ở tâm)

\(=> ∆AOB\) đều, nên \(AB = OA = OB = R.\)

Vì  \( sđ \overparen{BC} = {90^0} \Rightarrow \widehat {BOC} = {90^0}\) (góc ở tâm)

\(\Rightarrow BC = \sqrt{OB^2+OC^2}=R\sqrt2.\)

Kẻ \(OH \bot CD.\)

Tứ giác \(ABCD\) là hình thang cân \(\Rightarrow \widehat{BCD}=\widehat{ADC}=75^0.\)

Lại có \(\Delta BOC\) vuông cân tại \(O \Rightarrow \widehat{BCO}=45^0.\)

\(\Rightarrow \widehat{OCD}=\widehat{BCD}-\widehat{BCO}=75^0-45^0=30^0.\)

Xét \(\Delta OCH\) vuông tại \(H\) ta có:

\(HC=OC.\cos \widehat{OCH}=\dfrac{R\sqrt{3}}{2}.\)

Mà \(H\) là trung điểm của \(CD\) (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).

\(\Rightarrow CD=2.CH=R\sqrt3.\) 

Sachbaitap.com