Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 26, 27 SGK Toán 9 Cánh Diều tập 1
Một nhóm bạn trẻ cùng tham gia khởi nghiệp và dự định góp vốn là 240 triệu đồng, số tiền góp mỗi người là như nhau. Nếu có thêm 2 người tham gia cùng thì số tiền mỗi người góp giảm đi 4 triệu đồng. Hỏi nhóm bạn trẻ đó có bao nhiêu người?
Xem thêm: Bài tập cuối chương 1
Bài 1 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Nghiệm của phương trình \(\frac{1}{x} - \frac{3}{{2x}} = \frac{1}{6}\) là:
A. \(x = 3\)
B. \(x = - 3\)
C. \(x = 6\)
D. \(x = - 6\)
Phương pháp:
+ Tìm điều kiện xác định của phương trình.
+ Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu.
+ Giải phương trình vừa tìm được.
+ Kết luận nghiệm.
Lời giải:
Đáp án đúng là: B
Giải phương trình: 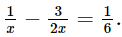
Điều kiện xác định: x ≠ 0.
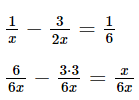
6 – 3.3 = x
6 – 9 = x
–3 = x.
Vậy phương trình đã cho có nghiệm là x = –3.
Bài 2 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 9\\x - y = - 1\end{array} \right.\) là:
A. \(\left( {x;y} \right) = \left( {4,5} \right)\);
B. \(\left( {x;y} \right) = \left( {5;4} \right)\);
C. \(\left( {x;y} \right) = \left( { - 5; - 4} \right)\);
D. \(\left( {x;y} \right) = \left( { - 4; - 5} \right)\)
Phương pháp:
Dùng máy tính cấm tay để tìm nghiệm của hệ phương trình.
Lời giải:
Đáp án đúng là: A
Giải hệ phương trình: 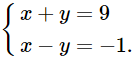
Cộng hai vế của hai phương trình trên, ta được phương trình: 2x = 8. (1)
Giải phương trình (1):
2x = 8
x = 4.
Thay x = 4 vào phương trình thứ nhất của hệ phương trình, ta được: 4 + y = 9. (2)
Giải phương trình (2):
4 + y = 9
y = 5.
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (4; 5).
Bài 3 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Giải các phương trình:
a. \(\left( {3x + 7} \right)\left( {4x + 9} \right) = 0\);
b. \(\left( {5x - 0,2} \right)\left( {0,3x + 6} \right) = 0\);
c. \(x\left( {2x - 1} \right) + 5\left( {2x - 1} \right) = 0\);
d. \({x^2} - 9 - \left( {x + 3} \right)\left( {3x + 1} \right) = 0\);
e. \({x^2} - 10x + 25 = 5\left( {5 - x} \right)\);
g. \(4{x^2} = {\left( {x - 12} \right)^2}\)
Phương pháp:
+ Chuyển phương trình về phương trình tích.
+ Giải các phương trình trong tích.
+ Kết luận nghiệm.
Lời giải:
a) (3x + 7)(4x – 9) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
3x + 7 = 0 3x = –7
|
4x – 9 = 0 4x = 9
|
Vậy phương trình đã cho có nghiệm là 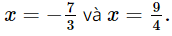
b) (5x – 0,2)(0,3x + 6) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
5x – 0,2 = 0 5x = 0,2 x = 0,04; |
0,3x + 6 = 0 0,3x = –6 x = –20. |
Vậy phương trình đã cho có nghiệm là x = 0,04 và x = –20.
c) x(2x – 1) + 5(2x – 1) = 0
(2x – 1)(x + 5) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
2x – 1 = 0 2x = 1
|
x + 5 = 0 x = –5. |
Vậy phương trình đã cho có nghiệm là 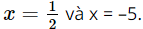
d) x2 – 9 – (x + 3)(3x + 1) = 0
(x + 3)(x – 3) – (x + 3)(3x + 1) = 0
(x + 3)(x – 3 – 3x – 1) = 0
(x + 3)(–2x – 4) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
x + 3 = 0 x = –3; |
–2x – 4 = 0 –2x = 4 x = –2. |
Vậy phương trình đã cho có nghiệm là x = –3 và x = –2.
e) x2 – 10x + 25 = 3(5 – x)
(x – 5)2 – 3(5 – x) = 0
(x – 5)2 + 3(x – 5) = 0
(x – 5)(x – 5 + 3) = 0
(x – 5)(x – 2) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
x – 5 = 0 x = 5; |
x – 2 = 0 x = 2. |
Vậy phương trình đã cho có nghiệm là x = 5 và x = 2.
g)
4x2 = (x – 12)2
(2x)2 – (x – 12)2 = 0
(2x – x + 12)(2x + x – 12) = 0
(x + 12)(3x – 12) = 0.
Để giải được phương trình trên, ta giải hai phương trình sau:
|
x + 12 = 0 x = –12; |
3x – 12 = 0 3x = 12 x = 4. |
Vậy phương trình đã cho có nghiệm là x = –12 và x = 4.
Bài 4 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Giải các phương trình :
a. \(\frac{{ - 6}}{{x + 3}} = \frac{2}{3}\);
b. \(\frac{{x - 2}}{2} + \frac{1}{{2x}} = 0\);
c. \(\frac{8}{{3x - 4}} = \frac{1}{{x + 2}}\);
d. \(\frac{x}{{x - 2}} + \frac{2}{{{{\left( {x - 2} \right)}^2}}} = 1\);
e. \(\frac{{3x - 2}}{{x + 1}} = 4 - \frac{{x + 2}}{{x - 1}}\);
g. \(\frac{{{x^2}}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} = 1 - \frac{1}{{x - 1}}\).
Phương pháp:
+ Tìm điều kiện xác định.
+ Tìm mẫu chung, quy đồng mẫu, khử mẫu.
+ Giải phương trình.
+ Đối chiếu với điều kiện xác định.
+ Kết luận nghiệm.
Lời giải:
a) Điều kiện xác định: x ≠ –3.
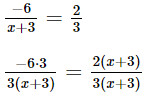
–6.3 = 2(x + 3)
–18 = 2x + 6
–2x = 24
x = –12 (thỏa mãn điều kiện x ≠ –3).
Vậy phương trình đã cho có nghiệm x = –12.
b) Điều kiện xác định: x ≠ 0.

(x – 2)x + 1 = 0
x2 – 2x + 1 = 0
(x – 1)2 = 0
x – 1 = 0
x = 1 (thỏa mãn điều kiện x ≠ 0).
Vậy phương trình đã cho có nghiệm x = 1.
c) Điều kiện xác định: 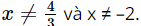
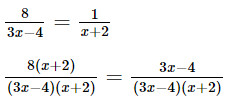
8(x + 2) = 3x – 4
8x + 16 = 3x – 4
5x = –20
x = –4 (thỏa mãn điều kiện 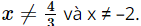 )
)
Vậy phương trình đã cho có nghiệm x = –4.
d) Điều kiện xác định: x ≠ 2.
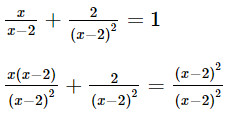
x(x – 2) + 2 = (x – 2)2
x2 – 2x + 2 = x2 – 4x + 4
2x = 2
x = 1 (thỏa mãn điều kiện x ≠ 2).
Vậy phương trình đã cho có nghiệm x = 1.
e) Điều kiện xác định: x ≠ –1 và x ≠ 1.
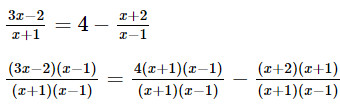
(3x – 2)(x – 1) = 4(x + 1)(x – 1) – (x + 2)(x + 1)
3x2 – 3x – 2x + 2 = 4(x2 – 1) – (x2 + x + 2x + 2)
3x2 – 5x + 2 = 4x2 – 4 – x2 – x – 2x – 2
3x2 – 5x – 4x2 + x2 + x + 2x = –4 – 2 – 2
–2x = –8
x = 4 (thỏa mãn điều kiện x ≠ –1 và x ≠ 1).
Vậy phương trình đã cho có nghiệm x = 4.
g) Điều kiện xác định: x ≠ 1 và x ≠ 2.
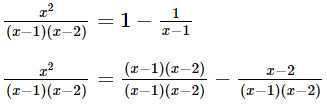
x2 = (x – 1)(x – 2) – (x – 2)
x2 = x2 – 2x – x + 2 – x + 2
x2 – x2 + 2x + x + x = 2 + 2
4x = 4
x = 1 (không thỏa mãn điều kiện x ≠ 1).
Vậy phương trình đã cho vô nghiệm.
Bài 5 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Giải các hệ phương trình:
a. \(\left\{ \begin{array}{l}x + 3y = - 2\\5x + 8y = 11\end{array} \right.\)
b. \(\left\{ \begin{array}{l}2x + 3y = - 2\\3x - 2y = - 3\end{array} \right.\)
c. \(\left\{ \begin{array}{l}2x - 4y = - 1\\ - 3x + 6y = 2\end{array} \right.\)
Phương pháp:
Giải hệ phương trình theo phương pháp thế hoặc phương pháp cộng đại số.
Lời giải:
a) Giải hệ phương trình: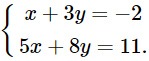
Nhân hai vế của phương trình thứ nhất với 5, ta được hệ phương trình sau: 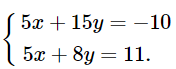
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta nhận được phương trình: 7y = –21 (1)
Giải phương trình (1):
7y = –21
y = –3.
Thay y = –3 vào phương trình x + 3y = –2, ta được: x + 3.(–3) = –2. (2)
Giải phương trình (2):
x + 3.(–3) = –2
x – 9 = –2
x = 7.
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (7; –3).
b) Giải hệ phương trình: 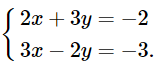
Nhân hai vế của phương trình thứ nhất với 3 và nhân hai vế của phương trình thứ hai với 2, ta được hệ phương trình sau:
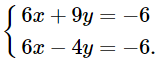
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta nhận được phương trình: 13y = 0 (3)
Giải phương trình (3):
13y = 0
y = 0.
Thay y = 0 vào phương trình 2x + 3y = –2, ta được: 2x + 3.0 = –2. (4)
Giải phương trình (4):
2x + 3.0 = –2
2x + 0 = –2
2x = –2
x = –1.
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (–1; 0).
c) Giải hệ phương trình: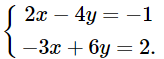
Nhân hai vế của phương trình thứ nhất với 3 và nhân hai vế của phương trình thứ hai với 2, ta được hệ phương trình sau:
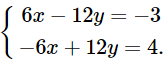
Cộng từng vế hai phương trình của hệ phương trình trên, ta nhận được phương trình:
0x + 0y = 1, hay 0x = 1. Phương trình này vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Bài 6 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Một nhóm bạn trẻ cùng tham gia khởi nghiệp và dự định góp vốn là 240 triệu đồng, số tiền góp mỗi người là như nhau. Nếu có thêm 2 người tham gia cùng thì số tiền mỗi người góp giảm đi 4 triệu đồng. Hỏi nhóm bạn trẻ đó có bao nhiêu người?
Phương pháp:
+ Gọi ẩn \(x\). Tìm điều kiện và đơn vị của ẩn.
+ Biểu diễn các đại lượng thông qua \(x\).
+ Tìm phương trình liên hệ.
+ Giải phương trình.
+ Đối chiếu với điều kiện của \(x\).
+ Kết luận bài toán.
Lời giải:
Gọi số người ban đầu của nhóm bạn trẻ đó là x (người) (x ∈ ℕ).
Lúc này, mỗi người góp số tiền là 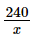 (triệu đồng).
(triệu đồng).
Nếu có thêm 2 người, nhóm bạn trẻ lúc này có số người là x + 2 (người).
Lúc đó, mỗi người góp số tiền là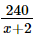 (triệu đồng).
(triệu đồng).
Theo bài, nếu có thêm 2 người tham gia cùng thì số tiền mỗi người góp giảm đi 4 triệu đồng nên ta có phương trình:
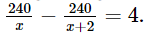
Giải phương trình:
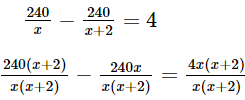
240(x + 2) – 240x = 4x(x + 2)
240x + 480 – 240x = 4x2 + 8x
4x2 + 8x – 480 = 0
x2 + 2x – 120 = 0
x2 – 10x + 12x – 120 = 0
x(x – 10) + 12(x – 10) = 0
(x – 10)(x + 12) = 0
x – 10 = 0 hoặc x + 12 = 0
x = 10 hoặc x = –12.
Ta thấy x = 10 thỏa mãn điều kiện x ∈ ℕ.
Vậy nhóm bạn trẻ đó có 10 người.
Bài 7 trang 26 SGK Toán 9 tập 1 - Cánh Diều
Một nhóm công nhân cần phải cắt cỏ ở một số mặt sân cỏ. Nếu nhóm công nhân đó sử dụng 3 máy cắt cỏ ngồi lái và 2 máy cắt cỏ đẩy tay trong 10 phút thì cắt được \(2990{m^2}\) cỏ. Nếu nhóm công nhân đó sử dụng 4 máy cắt cỏ ngồi lái và 3 máy cắt cỏ đẩy tay trong 10 phút thì cắt được \(4060{m^2}\) cỏ. Hỏi trong 10 phút, mỗi loại máy trên sẽ cắt được bao nhiêu mét vuông cỏ?

Phương pháp:
+ Gọi ẩn \(x,y\). Tìm đơn vị và điều kiện của \(x,y\).
+ Biểu diễn các đại lượng qua \(x,y\).
+ Viết hệ phương trình.
+ Giải hệ phương trình.
+ Kết luận bài toán.
Lời giải:
Gọi số m2 cỏ mà một cỏ máy cắt cỏ ngồi lái và một máy cắt cỏ đẩy tay cắt được trong 10 phút lần lượt là x, y (x > 0, y > 0).
Khi đó, trong 10 phút:
⦁ 3 máy cắt cỏ ngồi lái và 2 máy cắt cỏ đẩy tay cắt được 3x + 2y (m2 cỏ).
⦁ 4 máy cắt cỏ ngồi lái và 3 máy cắt cỏ đẩy tay cắt được 4x + 3y (m2 cỏ).
Theo bài, nếu nhóm công nhân đó sử dụng 3 máy cắt cỏ ngồi lái và 2 máy cắt cỏ đẩy tay trong 10 phút thì cắt được 2 990 m2 cỏ nên ta có phương trình 3x + 2y = 2 990.
Nếu nhóm công nhân đó sử dụng 4 máy cắt cỏ ngồi lái và 3 máy cắt cỏ đẩy tay trong 10 phút thì cắt được 4 060 m2 cỏ nên ta có phương trình 4x + 3y = 4 060.
Ta có hệ phương trình: 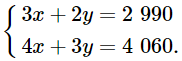
Nhân hai vế của phương trình thứ nhất với 3 và nhân hai vế của phương trình thứ hai với 2, ta được hệ phương trình sau:
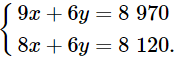
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta được phương trình: x = 850.
Thay x = 850 vào phương trình 3x + 2y = 2 990, ta được: 3 . 850 + 2y = 2 990. (1)
Giải phương trình (1):
3 . 850 + 2y = 2 990
2 550 + 2y = 2 990
2y = 440
y = 220.
Vậy trong 10 phút, một chiếc máy cắt cỏ ngồi lái cắt được 850 m2 cỏ và một chiếc máy cắt cỏ đẩy tay cắt được 220 m2 cỏ,
Bài 8 trang 27 SGK Toán 9 tập 1 - Cánh Diều
Tại một buổi biểu diễn nhằm gây quỹ từ thiện, ban tổ chức đã bán 500 vé. Trong đó có hai loại vé: vé loại I giá 100 000 đồng; vé loại II giá 75 000 đồng. Tổng số tiền thu được từ bán vé là 44 500 000 đồng. Tính số vé bán ra của mỗi loại.
Phương pháp:
+ Gọi ẩn \(x,y\). Tìm đơn vị và điều kiện của \(x,y\).
+ Biểu diễn các đại lượng qua \(x,y\).
+ Viết hệ phương trình.
+ Giải hệ phương trình.
+ Kết luận bài toán.
Lời giải:
Gọi số vé bán ra của vé loại I và vé loại II lần lượt là x, y (vé) (0 < x < 500, 0 < y < 500).
Theo bài, ban tổ chức đã bán được 500 vé cả hai loại vé nên ta có phương trình: x + y = 500.
Số tiền thu được khi bán ra x vé loại I là 100 000x (đồng).
Số tiền thu được khi bán ra y vé loại II là 75 000y (đồng).
Theo bài, tổng số tiền thu được từ bán vé là 44 500 000 đồng nên ta có phương trình:
100 000x + 75 000y = 44 500 000, hay 4x + 3y = 1 780.
Ta có hệ phương trình: 
Nhân hai vế của phương trình thứ nhất với 4, ta được hệ phương trình sau: 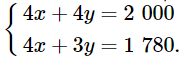
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta được phương trình: y = 220.
Thay y = 220 vào phương trình x + y = 500, ta được: 220 + y = 500. (1)
Giải phương trình (1):
220 + y = 500
y = 280.
Vậy vé loại I bán ra được 220 vé và vé loại 2 bán ra được 280 vé.
Bài 9 trang 27 SGK Toán 9 tập 1 - Cánh Diều
Trong một đợt khuyến mãi, siêu thị giảm giá cho mặt hàng A là 20% và mặt hàng B là 15% so với giá niêm yết. Một khách hàng mua 2 món hàng A và 1 món hàng B thì số tiền phải trả số tiền là 362 000 đồng. Nhưng nếu mua trong khung giờ vàng thì mặt hàng A được giảm giá 30% và mặt hàng B được giảm giá 25% so với giá niêm yết. Một khách hàng mua 3 món hàng A và 2 món hàng B trong khung giờ vàng nên phải trả số tiền là 552 000 đồng. Tính giá niêm yết của mỗi mặt hàng A và B.
Phương pháp:
+ Gọi ẩn \(x,y\). Tìm đơn vị và điều kiện của \(x,y\).
+ Biểu diễn các đại lượng qua \(x,y\).
+ Viết hệ phương trình.
+ Giải hệ phương trình.
+ Kết luận bài toán.
Lời giải:
Gọi giá niêm yết của mặt hàng A và mặt hàng B lần lượt là x, y (đồng) (x > 0, y > 0).
Mặt hàng A sau khi giảm 20% giá niêm yết thì có giá là x.(100% – 20%) = x.80% = 0,8x (đồng).
Mặt hàng B sau khi giảm 15% giá niêm yết thì có giá là y.(100% – 15%) = y.85% = 0,85y (đồng).
Theo bài, khách hàng mua 2 món hàng A và 1 món hàng B thì phải trả số tiền là 362 000 đồng nên ta có phương trình:
2.0,8x + 0,85y = 362 000, hay 1,6x + 0,85y = 362 000.
Nếu mua trong khung giờ vàng:
⦁ mặt hàng A được giảm giá 30% so với giá niêm yết nên lúc này, mặt hàng A có giá là x.(100% – 30%) = x.70% = 0,7x (đồng).
⦁ mặt hàng B được giảm giá 25% so với giá niêm yết nên lúc này, mặt hàng B có giá là x.(100% – 25%) = x.75% = 0,75y (đồng).
Theo bài, khách hàng mua 3 món hàng A và 2 món hàng B trong khung giờ vàng trả số tiền là 552 000 đồng nên ta có phương trình:
3.0,7x + 2.0,75y = 552 000, hay 2,1x + 1,5y = 552 000.
Ta có hệ phương trình: 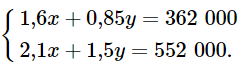
Nhân hai vế của phương trình thứ nhất với 210 và nhân hai vế của phương trình thứ hai với 160, ta được hệ phương trình sau: 
Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất, ta được phương trình:
61,5y = 12 300 000. (1)
Giải phương trình (1):
61,5y = 12 300 000
y = 200 000.
Thay y = 200 000 vào phương trình 1,6x + 0,85y = 362 000, ta được:
1,6x + 0,85 . 200 000 = 362 000. (2)
Giải phương trình (2):
1,6x + 0,85 . 200 000 = 362 000
1,6x + 170 000 = 362 000
1,6x = 192 000
x = 120 000.
Vậy giá niêm yết của mặt hàng A là 120 000 đồng và giá niêm yết của mặt hàng B là 200 000 đồng.
Bài 10 trang 27 SGK Toán 9 tập 1 - Cánh Diều
Trong phòng thí nghiệm, cô Linh muốn tạo ra 500g dung dịch HCl 19% từ hai loại dung dịch HCl 10% và HCl 25%. Hỏi cô Linh cần dùng bao nhiêu gam cho mỗi loại dung dịch đó?
Phương pháp:
+ Gọi ẩn \(x,y\). Tìm đơn vị và điều kiện của \(x,y\).
+ Biểu diễn các đại lượng qua \(x,y\).
+ Viết hệ phương trình.
+ Giải hệ phương trình.
+ Kết luận bài toán.
Lời giải:
Gọi khối lượng dung dịch HCl có nồng động 10% và 25% mà cô Linh cần dùng là x, y (g) (0 < x < 500, 0 < y < 500).
Theo bài, khi trộn hai dung dịch trên thì được 500 g dung dịch HCl 19% nên ta có phương trình: x + y = 500.
Khối lượng HCl có trong x g dung dịch nồng độ 10% là x.10% = 0,1x (g).
Khối lượng HCl có trong y g dung dịch nồng độ 25% là y.25% = 0,25y (g).
Khối lượng HCK có trong 500 g dung dịch nồng độ 19% là 500.19% = 95 (g).
Khi đó ta có phương trình: 0,1x + 0,25y + 95.
Ta có hệ phương trình: 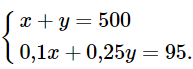
Nhân hai vế của phương trình thứ nhất với 0,25, ta nhận được hệ phương trình sau: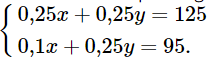
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta nhận được phương trình: 0,15x = 30. (1)
Giải phương trình (1):
0,15x = 30
x = 200.
Thay x = 200 vào phương trình x + y = 500, ta được 200 + y = 500, (2)
Giải phương trình (2):
200 + y = 500
y = 200.
Ta thấy x = 200 và y = 300 thỏa mãn điều kiện.
Vậy cô Linh cần dùng 200 g dung dịch HCl 10% và 300 dung dịch HCl 25%.
Bài 11 trang 27 SGK Toán 9 tập 1 - Cánh Diều
Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B và lại ngược dòng từ địa điểm B về địa điểm A mất 9 giờ, tốc độ của ca nô khi nước yên lặng không đổi trên suốt quãng đường đó và tốc độ của dòng nước không đổi khi ca nô chuyển động. Biết thời gian ca nô đi xuôi dòng 5km bằng thời gian ca nô đi ngược dòng 4km và quãng đường AB là 160km. Tính tốc độ của ca nô khi nước yên lặng và tốc độ của dòng nước.
Phương pháp:
+ Gọi ẩn \(x,y\). Tìm đơn vị và điều kiện của \(x,y\).
+ Biểu diễn các đại lượng qua \(x,y\).
+ Viết hệ phương trình.
+ Giải hệ phương trình.
+ Kết luận bài toán.
Lời giải:
Gọi tốc độ của ca nô khi nước yên lặng và tốc độ của dòng nước lần lượt là x, y (km/h) (x > y > 0).
Tốc độ của ca nô khi đi xuôi dòng là x + y (km/h).
Tốc độ của ca nô khi đi ngược dòng là x – y (km/h).
Thời gian ca nô đi xuôi dòng quãng đường AB là 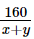 (giờ).
(giờ).
Thời gian ca nô đi ngược dòng quãng đường AB là 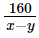 (giờ).
(giờ).
Theo bài, thời gian cả đi và về là 9 giờ nên ta có phương trình: 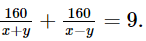
Thời gian ca nô đi xuôi dòng quãng đường 5 km là 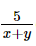 (giờ).
(giờ).
Thời gian ca nô đi ngược dòng quãng đường 4 km là 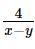 (giờ).
(giờ).
Theo bài, thời gian ca nô đi xuôi dòng 5 km bằng thời gian ca nô đi ngược dòng 4 km nên ta có phương trình: 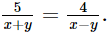
Ta có hệ phương trình: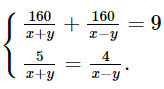

Cộng từng vế của hai phương trình của hệ trên, ta nhận được phương trình: 2x = 72. (5)
Giải phương trình (5):
2x = 72
x = 36.
Thay x = 36 vào phương trình x – y = 32, ta được 36 – y = 32. (6)
Giải phương trình (6):
36 – y = 32
y = 4.
Ta thấy x = 36 và y = 4 thỏa mãn điều kiện x > y > 0.
Vậy tốc độ của ca nô khi nước yên lặng là 36 km/h và tốc độ của dòng nước là 4 km/h.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 124, 125 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4 trang 122, 123 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5, 6 trang 117 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 109, 110 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 104 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Bài tập cuối chương 5
- Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
- Bài 4: Góc ở tâm. Góc nội tiếp
- Bài 3: Tiếp tuyến của đường tròn
- Bài 2: Vị trí tương đối của đường thẳng và đường tròn
- Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
- Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!