Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 42, 43 SGK Toán 9 Cánh Diều tập 1
Đến ngày 31/12/2022, gia đình bác Hoa đã tiết kiệm được số tiền là 250 triệu đồng. Sau thời điểm đó, mỗi tháng gia đình bác Hoa đều tiết kiệm được 10 triệu đồng. Gia đình bác Hoa dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá tối thiểu là 370 triệu đồng.
Xem thêm: Bài tập cuối chương 2
Bài 1 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Cho bất đẳng thức \(a > b\). Kết luận nào sau đây là không đúng?
A. \(2a > 2b\)
B. \( - a < - b\)
C. \(a - 3 < b - 3\)
D. \(a - b > 0\)
Phương pháp:
Dựa vào tính chất của bất đẳng thức để chứng minh.
Lời giải:
Đáp án đúng là: C
Do a > b nên a – 3 > b – 3.
Vậy kết luận ở phương án C là không đúng.
Bài 2 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a. Bất phương trình \(ax + b < 0\) với \(a > 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
b. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x < \frac{{ - b}}{a}\).
c. Bất phương trình \(ax + b < 0\) với \(a < 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).
d. Bất phương trình \(ax + b < 0\) với \(a \ne 0\) có nghiệm là \(x > \frac{{ - b}}{a}\).
Phương pháp:
Dựa vào cách giải bất phương trình tổng quát để xác định phát biểu đúng, sai
Lời giải:
⦁ Xét bất phương trình: ax + b < 0 với a > 0.
ax + b < 0
ax < –b
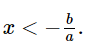
⦁ Xét bất phương trình: ax + b < 0 với a < 0.
ax + b < 0
ax < –b
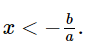
Vậy trong các khẳng định đã cho, khẳng định a và c là khẳng định đúng; khẳng định b và khẳng định d là sai.
Bài 3 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Chứng minh:
a. Nếu \(a > 5\) thì \(\frac{{a - 1}}{2} - 2 > 0\).
b. Nếu \(b > 7\) thì \(4 - \frac{{b + 3}}{5} < 2\).
Phương pháp:
Giải bất phương trình để chứng minh.
Lời giải:
a) Do a > 5, nên a – 1 > 4, suy ra 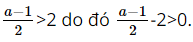
b) Do b > 7, nên b + 3 > 10, suy ra 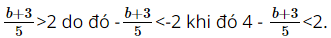
Bài 4 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Cho \(4,2 < a < 4,3\). Chứng minh: \(13,8 < 3a + 1,2 < 14,1\).
Phương pháp:
Sử dụng các tính chất bất đẳng thức để chứng minh.
Lời giải:
Do 4,2 < a nên 12,6 < 3a, suy ra 13,8 < 3a + 1,2.
Do a < 4,3 nên 3a < 12,9, suy ra 3a + 1,2 < 14,1.
Vậy 13,8 < 3a + 1,2 < 14,1.
Bài 5 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Cho \(a \ge 2\). Chứng minh:
a. \({a^2} \ge 2a\)
b. \({\left( {a + 1} \right)^2} \ge 4a + 1\)
Phương pháp:
Xét hiệu của 2 vế để chứng minh.
Lời giải:
a) Do a ≥ 2 nên a.a ≥ 2a hay a2 ≥ 2a.
b) Xét hiệu (a + 1)2 – (4a + 1) = a2 + 2a + 1 – 4a – 1 = a2 – 2a = a(a – 2).
Do a ≥ 2 nên a – 2 ≥ 0.
Suy ra a.(a – 2) ≥ 0 nên (a + 1)2 – (4a + 1) ≥ 0.
Vậy (a + 1)2 ≥ 4a + 1.
Bài 6 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Chứng minh nửa chu vi của một tam giác lớn hơn độ dài mỗi cạnh của tam giác đó.
Phương pháp:
Gọi ẩn rồi biểu diễn các đại lượng theo ẩn rồi giải bất phương trình.
Lời giải:
Gọi độ dài ba cạnh của tam giác là a, b, c (a, b, c > 0).
Theo bất đẳng thức trong tam giác, ta có: a + b > c.
Suy ra a + b + c > 2c
Do đó 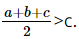
Chứng minh tương tự ta cũng có 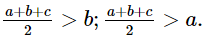
Vậy nửa chu vi của một tam giác lớn hơn độ dài mỗi cạnh của tam giác đó.
Bài 7 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Giải các bất phương trình:
a. \(5 + 7x \le 11\);
b. \(2,5x - 6 > 9 + 4x\);
c. \(2x - \frac{{x - 7}}{3} < 9\);
d. \(\frac{{3x + 5}}{2} + \frac{x}{5} - 0,2x \ge 4\).
Phương pháp:
Dựa vào cách giải bất phương trình tổng quát để giải bất phương trình.
Lời giải:
a) 5 + 7x ≤ 11
7x ≤ 6
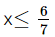
Vậy nghiệm của bất phương trình đã cho là 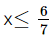
b) 2,5x – 6 > 9 + 4x
2,5x – 4x > 9 + 6
–1,5x > 15
x < –10.
Vậy nghiệm của bất phương trình đã cho là x < –10.
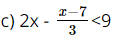
3.2x – (x – 7) < 9.3
6x – x + 7 < 27
5x < 20
x < 4.
Vậy nghiệm của bất phương trình đã cho là x < 4.
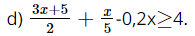
5.(3x + 5) + 2.x – 0,2x.10 ≥ 4.10
15x + 25 + 2x – 2x ≥ 40
15x ≥ 15
x ≥ 1.
Vậy nghiệm của bất phương trình đã cho là x ≥ 1.
Bài 8 trang 42 SGK Toán 9 tập 1 - Cánh Diều
Để đổi từ độ Fahrenheit (Độ F) sang độ Celsius (Độ C), người ta dùng công thức sau: \(C = \frac{5}{9}\left( {F - 32} \right)\).
a. Giả sử nhiệt độ ngoài trời của một ngày mùa hè ít nhất là \(95^\circ F\). Hỏi nhiệt độ ngoài trời khi đó ít nhất là bao nhiêu độ C?
b. Giả sử nhiệt độ ngoài trời của một ngày mùa hè ít nhất là \(36^\circ C\). Hỏi nhiệt độ ngoài trời khi đó ít nhất là bao nhiêu độ F?
Phương pháp:
Thay số rồi giải bất phương trình để giải bài toán.
Lời giải:
a) Theo bài, F ≥ 95 nên F – 32 ≥ 95 – 32 hay F – 32 ≥ 63.
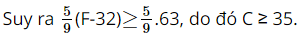
Vậy nhiệt độ ngoài trời của một ngày mùa hè ít nhất là 95°F, tức ít nhất là 35°C.
b) Theo bài, C ≥ 95 nên 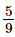 (F-32)≥">≥95.
(F-32)≥">≥95.
Giải bất phương trình:
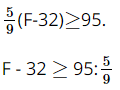
F – 32 ≥ 171
F ≥ 203.
Vậy nhiệt độ ngoài trời của một ngày mùa hè ít nhất là 95°C, tức là ít nhất là 203°F.
Bài 9 trang 43 SGK Toán 9 tập 1 - Cánh Diều
Một nhà máy sản xuất xi măng mỗi ngày đều sản xuất được 100 tấn xi măng. Lượng xi măng tồn trong kho của nhà máy là 300 tấn. Hỏi nhà máy đó cần ít nhất bao nhiêu ngày để có thể xuất đi 15 300 tấn xi măng (tính cả lượng tồn trong kho)?
Phương pháp:
+ Đặt ẩn \(x\);
+ Biểu diễn các đại lượng theo \(x\);
+ Giải bất phương trình;
+ Kết luận bài toán.
Lời giải:
Gọi x (ngày) là số ngày sản xuất xi măng của nhà máy đó (x > 0).
Khối lượng xi măng sản xuất được sau x ngày là: 100x (tấn).
Khối lượng xi măng tính cả lượng xi măng tồn trong kho sau x ngày là: 100x + 300 (tấn).
Theo bài, sau x ngày thì nhà máy xuất đi ít nhất 15 300 tấn xi măng nên ta có bất phương trình: 100x + 300 ≥ 15 300.
Giải bất phương trình:
100x + 300 ≥ 15 300
100x ≥ 15 000
x ≥ 150.
Vậy nhà máy đó cần sản xuất trong ít nhất là 150 ngày để có thể xuất đi 15 300 tấn xi măng (tính cả lượng xi măng tồn trong kho).
Bài 10 trang 43 SGK Toán 9 tập 1 - Cánh Diều
Đến ngày 31/12/2022, gia đình bác Hoa đã tiết kiệm được số tiền là 250 triệu đồng. Sau thời điểm đó, mỗi tháng gia đình bác Hoa đều tiết kiệm được 10 triệu đồng. Gia đình bác Hoa dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hóa với giá tối thiểu là 370 triệu đồng. Hỏi sau ít nhất bao nhiêu tháng gia đình bác Hoa có thể mua được chiếc ô tô đó bằng số tiền tiết kiệm được?
Phương pháp:
+ Đặt ẩn \(x\);
+ Biểu diễn các đại lượng theo \(x\);
+ Giải bất phương trình;
+ Kết luận bài toán.
Lời giải:
Gọi x (tháng) là thời gian gia đình bác Hoa có thể mua được chiếc ô tô tải bằng số tiền tiết kiệm được.
Sau x tháng, số tiền gia đình bác Hoa tiết kiệm được là: 10x (triệu đồng).
Khi đó tổng số tiền gia đình bác Hoa tiết kiệm được là: 250 + 10x (triệu đồng).
Theo bài, gia đình bác Hoa dự định mua một chiếc ô tô tải nhỏ để vận chuyển hàng hoá với giá tối thiểu là 370 triệu đồng nên ta có bất phương trình:
250 + 10x ≥ 370.
Giải bất phương trình:
250 + 10x ≥ 370
10x ≥ 120
x ≥ 12.
Vậy sau ít nhất 12 tháng, gia đình bác Hoa có thể mua được chiếc ô tô tải đó bằng số tiền tiết kiệm được.
Bài 11 trang 43 SGK Toán 9 tập 1 - Cánh Diều
Chỉ số khối cơ thể, thường được biết đến với tên viết tắt BMI (tiếng Anh là Body Mass Index) cho phép đánh giá thể trạng của một người là gầy, bình thường hay béo. Chỉ số khối cơ thể của một người được tính theo công thức sau: \(BMI = \frac{m}{{h{}^2}}\), trong đó m là khố lượng cơ thể tính theo kilôgam, h là chiều cao tính theo mét.
Dưới đây là bảng đánh giá thể trạng ở người lớn theo BMI đối với khu vực châu Á – Thái Bình Dương:
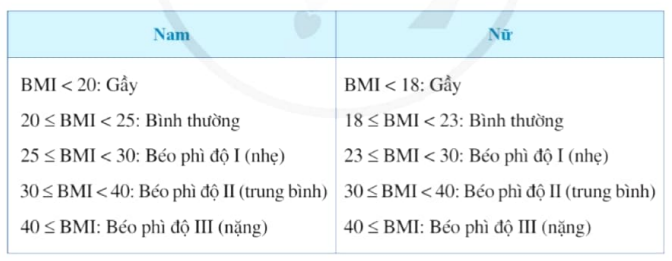

a. Giả sử một người đàn ông có chiều cao 1,68m. Hãy lập bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng trên.
b. Giả sử một người phụ nữ có chiều cao 1,6m. Hãy lập bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng trên.
Phương pháp:
Thay số vào công thức để xét.
Lời giải:
a) Thay h = 1,68 m vào biểu thức 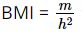 ta được:
ta được:
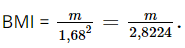
⦁ Khi BMI < 20 thì 2,8224.BMI < 56,448 hay m < 56,448.
⦁ Khi 20 ≤ BMI < 25 thì 56,448 ≤ 2,8224.BMI < 70,56 hay 56,448 ≤ m < 70,56.
⦁ Khi 25 ≤ BMI < 30 thì 70,56 ≤ 2,8224.BMI < 84,672 hay 70,56 ≤ m < 84,672.
⦁ Khi 30 ≤ BMI < 40 thì 84,672 ≤ 2,8224.BMI < 112,896 hay 84,672 ≤ m < 112,896.
⦁ Khi 40 ≤ BMI thì 112,896 ≤ 2,8224.BMI hay 112,896 ≤ m.
Vậy ta có bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng như sau:
|
Cân nặng |
Thể trạng |
|
m < 56,448 |
Gầy |
|
56,448 ≤ m < 70,56 |
Bình thường |
|
70,56 ≤ m < 84,672 |
Béo phì độ I (nhẹ) |
|
84,672 ≤ m < 112,896 |
Béo phì độ II (trung bình) |
|
112,896 ≤ m |
Béo phì độ III (nặng) |
b) Thay h = 1,6 m vào biểu thức 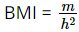 ta được:
ta được:
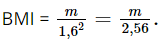
Suy ra m = 2,56.BMI.
⦁ Khi BMI < 18 thì 2,56.BMI < 46,08 hay m < 46,08.
⦁ Khi 18 ≤ BMI < 23 thì 46,08 ≤ 2,56.BMI < 58,88 hay 46,08 ≤ m < 58,88.
⦁ Khi 23 ≤ BMI < 30 thì 58,88 ≤ 2,56.BMI < 76,8 hay 58,88 ≤ m < 76,8.
⦁ Khi 30 ≤ BMI < 40 thì 76,8 ≤ 2,56.BMI < 102,4 hay 76,8 ≤ m < 102,4.
⦁ Khi 40 ≤ BMI thì 102,4 ≤ 2,56.BMI hay 102,4 ≤ m.
Vậy ta có bảng về chỉ số cân nặng của người đó dựa theo bảng đánh giá thể trạng như sau:
|
Cân nặng |
Thể trạng |
|
m < 46,08 |
Gầy |
|
46,08 ≤ m < 58,88 |
Bình thường |
|
58,88 ≤ m < 76,8 |
Béo phì độ I (nhẹ) |
|
76,8 ≤ m < 102,4 |
Béo phì độ II (trung bình) |
|
102,4 ≤ m |
Béo phì độ III (nặng) |
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 124, 125 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4 trang 122, 123 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5, 6 trang 117 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 109, 110 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 104 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Bài tập cuối chương 5
- Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
- Bài 4: Góc ở tâm. Góc nội tiếp
- Bài 3: Tiếp tuyến của đường tròn
- Bài 2: Vị trí tương đối của đường thẳng và đường tròn
- Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
- Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!