Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 81 SGK Toán 9 Cánh Diều tập 1

Bài 1 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 4cm,BC = 6cm\). Tính các tỉ số lượng giác của góc \(B\).

Phương pháp:

Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.

Lời giải:

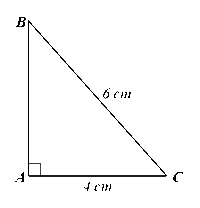
Xét ∆ABC vuông tại A, theo định lý Pythagore, ta có:

BC² = AB² + AC²

Suy ra AB² = BC² – AC² = 6² – 4² = 20.

Do đó AB =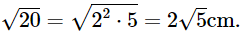

Xét ∆ABC vuông tại A, ta có:

Bài 2 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 2cm,AC = 3cm\). Tính các tỉ số lượng giác của góc \(C\).

Phương pháp:

Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.

Lời giải:

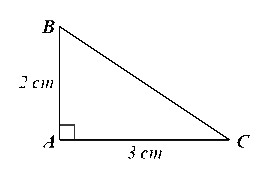
Xét ∆ABC vuông tại A, theo định lý Pythagore, ta có:

BC² = AB² + AC² = 2² + 3² = 13.

Suy ra BC =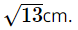

Xét ∆ABC vuông tại A, ta có:

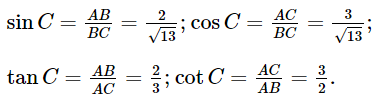
Bài 3 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Cho tam giác \(MNP\) có \(MN = 5cm,MP = 12cm,NP = 13cm\). Chứng minh tam giác \(MNP\) vuông tại \(N\). Từ đó, tính các tỉ số lượng giác của góc \(N\).

Phương pháp:

Áp dụng định lý Pythagore đảo để chứng minh tam giác \(MNP\) vuông tại \(N\).

Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.

Lời giải:

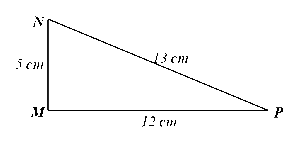
Xét ∆MNP, ta có: NP² = 13² = 169 và MN² + MP² = 5² + 12² = 169.

Suy ra NP² = MN² + MP².

Do đó ∆MNP vuông tại M (định lí Pythagore đảo).

Khi đó:

Bài 4 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc \(63^\circ \)? Vì sao?

a) \(\sin 27^\circ \)

b) \(\cos 27^\circ \)

c) \(\tan 27^\circ \)

d) \(\cot 27^\circ \)

Phương pháp:

Dựa vào tỉ số lượng giác của các góc phụ nhau để tính.

Lời giải:

Vì 27° và 63° là hai góc phụ nhau nên ta có:

a) sin27° = cos63°;

b) cos27° = sin63°;

c) tan27° = cot63°;

d) cot27° = tan63°.

Bài 5 trang 81 SGK Toán 9 tập 1 - Cánh Diều

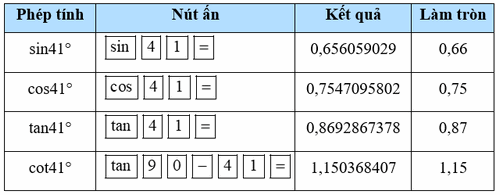
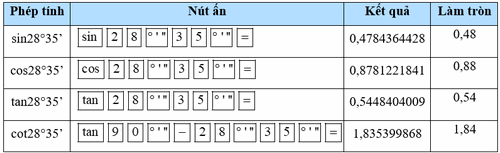
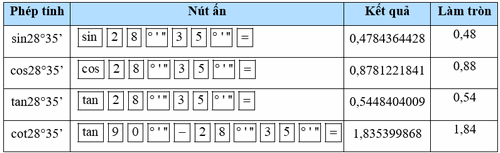
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):

a) \(41^\circ \)

b) \(28^\circ 35'\)

c) \(70^\circ 27'46''\)

Phương pháp:

Dựa vào cách bấm máy tính để tính từng tỉ số lượng giác.

Lời giải:

a)

b)

c)

Bài 6 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị biểu thức:

\(A = \sin 25^\circ  + \cos 25^\circ  - \sin 65^\circ  - \cos 65^\circ \).

Phương pháp:

Dựa vào tỉ số lượng giác của các góc phụ nhau để tính.

Lời giải:

Vì25° và 65° là hai góc phụ nhau nên ta có sin25° = cos65° và sin65° = cos25°.

Do đó:

A = sin25° + cos25° – sin65° – cos65°

= cos65° + cos25° – cos25° – cos65°

= 0.

Bài 7 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Cho góc nhọn \(\alpha \). Biết rằng, tam giác \(ABC\) vuông tại \(A\) sao cho \(\widehat B = \alpha \).

a) Biểu diễn các tỉ số lượng giác của góc nhọn \(\alpha \) theo \(AB,BC,CA\).

b) Chứng minh: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\); \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\); \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\); \(\tan \alpha .\cot \alpha  = 1\).

Từ đó, tính giá trị biểu thức: \(S = {\sin ^2}35^\circ  + {\cos ^2}35^\circ \); \(T = \tan 61^\circ .\cot 61^\circ \).

Phương pháp:

Dựa vào định nghĩa tỉ số lượng giác để làm bài toán.

Lời giải:

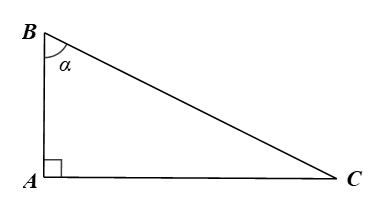
a) Xét ∆ABC vuông tại A, ta có:

b) Xét ∆ABC vuông tại A, ta có:

⦁ BC² = AB² + AC² (định lí Pythagore);

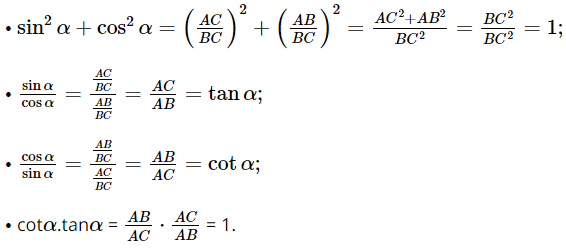
Ta có: S = sin²35° + cos²35° = 1; T = tan61°.cot61° = 1.

Bài 8 trang 81 SGK Toán 9 tập 1 - Cánh Diều

Hình 11 mô tả tia nắng mặt trời dọc theo \(AB\) tạo với phương nằm ngang trên mặt đất một góc \(\alpha  = \widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc \(\alpha \) (làm tròn kết quả đến hàng đơn vị của độ), biết \(AH = 2m,BH = 5m\).

Phương pháp:

Thay số rồi giải bất phương trình để giải bài toán.

Lời giải:

Xét ∆ABH vuông tại H, ta có tanB =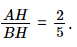 

Suy ra α ≈ 22°. 

Sachbaitap.com