Giải bài 1, 2, 3, 4, 5, 6, 7 trang 99, 100 SGK Toán 9 Cánh Diều tập 1
Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn. Quan sát Hình 18 và chỉ ra một cặp đường tròn: a) Cắt nhau;b) Tiếp xúc ngoài; c) Tiếp xúc trong; d) Không giao nhau.
Bài 1 trang 99 SGK Toán 9 tập 1 - Cánh Diều
Trong Hình 16, có ba đường tròn với các đường kính lần lượt là \(AB,AC,CD\). Hãy sắp xếp độ dài ba đoạn thẳng \(AB,AC,CD\) theo thứ tự tăng dần và giải thích kết quả tìm được.
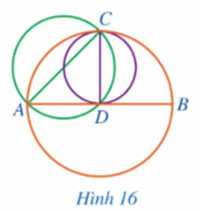

Phương pháp:
Dựa vào mối liên hệ giữa đường kính và dây để so sánh.
Lời giải:
Xét đường tròn đường kính AC, có dây cung CD, do đó CD < AC (trong các dây của đường tròn, dây lớn nhất là đường kính).
Xét đường tròn đường kính AB, có dây cung AC, do đó AC < AB (trong các dây của đường tròn, dây lớn nhất là đường kính).
Do đó CD < AC < AB.
Bài 2 trang 100 SGK Toán 9 tập 1 - Cánh Diều
Xác định vị trí tương đối của hai đường tròn trong mỗi hình \(17a,17b,17c,17d\):
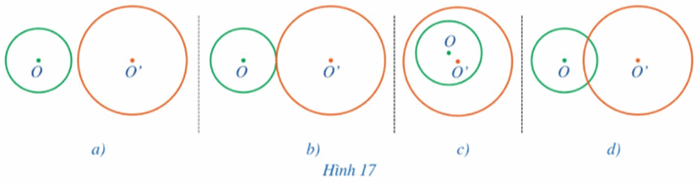

Phương pháp:
Dựa vào kiến thức “Vị trí tương đối của hai đường tròn gồm: cắt nhau, tiếp xúc trong, tiếp xúc ngoài, ở ngoài nhau, đựng” để xác định vị trí.
Lời giải:
a) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) không có điểm chung;
⦁ OO’ > R + R’.
Do đó hai đường tròn (O) và (O’) ở ngoài nhau.
b) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) có 1 điểm chung duy nhất;
⦁ OO’ = R + R’.
Do đó hai đường tròn (O) và (O’) tiếp xúc ngoài.
c) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) không có điểm chung;
⦁ OO’ < R’ – R.
Do đó đường tròn (O’) đựng đường tròn (O).
d) Ta thấy hai đường tròn (O) và (O’) có 2 điểm chung nên hai đường tròn (O) và (O’) cắt nhau.
Bài 3 trang 100 SGK Toán 9 tập 1 - Cánh Diều
Cho đoạn thẳng \(MN\) và đường thẳng \(a\) là đường trung trực của đoạn thẳng \(MN\). Điểm \(O\) thuộc đường thẳng \(a\).
a) Vẽ đường tròn tâm \(O\) bán kính \(R = OM\).
b) Chứng minh điểm \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Phương pháp:
Dựa vào tính chất đối xứng của đường tròn để chứng minh.
Lời giải:
a) Hình vẽ:
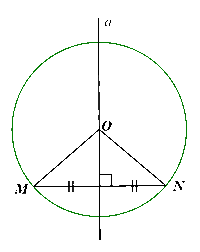
b) Vì O nằm đường trung trực của đoạn thẳng MN nên OM = ON.
Mà OM = R (câu a) nên ON = R.
Vậy N thuộc đường tròn (O; R).
Bài 4 trang 100 SGK Toán 9 tập 1 - Cánh Diều
Cho đường tròn \(\left( {O;R} \right)\) và dây\(AB = R\). Tính số đo góc \(AOB\).
Phương pháp:
Dựa vào tính chất của tam giác để tính.
Lời giải:
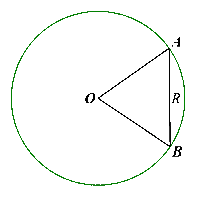
Vì AB là dây cung của đường tròn (O; R) nên OA = OB = R.
Mà AB = R nên OA = OB = AB = R.
Xét ∆OAB có OA = OB = AB = R nên ∆OAB là tam giác đều, suy ra
Bài 5 trang 100 SGK Toán 9 tập 1 - Cánh Diều
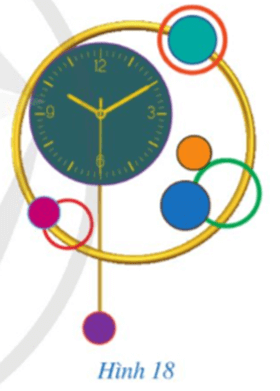
Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn. Quan sát Hình 18 và chỉ ra một cặp đường tròn:

a) Cắt nhau;
b) Tiếp xúc ngoài;
c) Tiếp xúc trong;
d) Không giao nhau.
Phương pháp:
Dựa vào kiến thức “Vị trí tương đối của hai đường tròn gồm: cắt nhau, tiếp xúc trong, tiếp xúc ngoài, ở ngoài nhau, đựng” để xác định vị trí.
Lời giải:
a) Một cặp đường tròn cắt nhau: Đường tròn màu đỏ và đường tròn màu vàng (khung đồng hồ).
b) Một cặp đường tròn tiếp xúc ngoài: Đường tròn màu xanh lá và đường tròn màu cam.
c) Một cặp đường tròn tiếp xúc trong: Đường tròn màu xanh cổ vịt (mặt đồng hồ) và đường tròn màu vàng (khung đồng hồ).
d) Một cặp đường tròn không giao nhau: Đường tròn màu vàng và đường tròn màu tím (quả lắc).
Bài 6 trang 100 SGK Toán 9 tập 1 - Cánh Diều
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) khác đường kính. Gọi \(M\) là trung điểm của \(AB\).
a) Đường thẳng \(OM\) có phải là đường trung trực của đoạn thẳng \(AB\) hay không? Vì sao?
b) Tính khoảng cách từ điểm \(O\) đến đường thẳng \(AB\), biết \(R = 5cm,AB = 8cm\).
Phương pháp:
Dựa vào các kiến thức đã học để giải bài toán.
Lời giải:
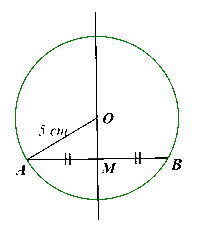
a) Vì AB là dây cung của đường kính (O; R) nên ta có OA = OB = R.
Khi đó, O nằm trên đường trung trực của AB.
Lại có M là trung điểm của AB nên M cũng nằm trên đường trung trực của AB.
Do đó OM là đường trung trực của đoạn thẳng AB.
b) Vì M là trung điểm của AB nên ta có MA = MB = 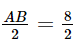 = 4 (cm).
= 4 (cm).
Vì OM là đường trung trực của đoạn thẳng AB nên OM ⊥ AB hay ∆OAM vuông tại M.
Theo định lí Pythagore ta có: OA2 = OM2 + AM2
Suy ra OM2 = OA2 – AM2 = 52 – 42 = 9.
Do đó OM = 3 cm.
Vậy khoảng cách từ điểm O đến đường thẳng AB là 3 cm.
Bài 7 trang 100 SGK Toán 9 tập 1 - Cánh Diều
Cho hai đường tròn cùng tâm \(\left( {O;R} \right),\left( {O;r} \right)\) với \(R > r\). Các điểm \(A,B\) thuộc đường tròn \(\left( {O;R} \right)\), các điểm \(A',B'\) thuộc đường tròn \(\left( {O;r} \right)\) sao cho \(O,A,A'\) thẳng hàng; \(O,B,B'\) thẳng hàng và điểm \(O\) không thuộc đường thẳng \(AB\). Chứng minh:
a) \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\).
b) \(AB//A'B'\).
Phương pháp:
Dựa vào các kiến thức đã học để giải bài toán.
Lời giải:
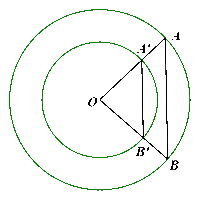
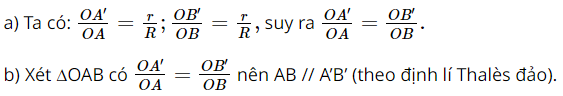
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 124, 125 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4 trang 122, 123 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5, 6 trang 117 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 109, 110 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Giải bài 1, 2, 3, 4, 5 trang 104 SGK Toán 9 Cánh Diều tập 1 (29/07)
- Bài tập cuối chương 5
- Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
- Bài 4: Góc ở tâm. Góc nội tiếp
- Bài 3: Tiếp tuyến của đường tròn
- Bài 2: Vị trí tương đối của đường thẳng và đường tròn
- Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
- Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
