Giải bài 1, 2, 3, 4, 5 trang 19, 20 SGK Toán 6 tập 2 Cánh Diều
Giải SGK Toán lớp 6 trang 19, 20 tập 1 Cánh Diều - Bài 4. Xác suất thực nghiệm trong một trò chơi và thí nghiệm đơn giản. Bài 5. a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?
Bài 1 trang 19 SGK Toán 6 tập 2 - Cánh Diều
Tung một đồng xu 20 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
? |
? |
? |
|
... |
? |
Tính xác suất thực nghiệm:
a) Xuất hiện mặt N; b) Xuất hiện mặt S;
Phương pháp:
*Xác suất thực nghiệm xuất hiện mặt N bằng
Số lần xuất hiện mặt N : Tổng số lần tung đồng xu
*Xác suất thực nghiệm xuất hiện mặt S bằng
Số lần xuất hiện mặt S : Tổng số lần tung đồng xu
Lời giải:
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
N |
11 |
9 |
|
2 |
S |
||
|
3 |
N |
||
|
4 |
N |
||
|
5 |
S |
||
|
6 |
S |
||
|
7 |
N |
||
|
8 |
S |
||
|
9 |
N |
||
|
10 |
N |
||
|
11 |
S |
||
|
12 |
S |
||
|
13 |
N |
||
|
14 |
N |
||
|
15 |
S |
||
|
16 |
S |
||
|
17 |
N |
||
|
18 |
N |
||
|
19 |
N |
||
|
20 |
S |
Xác suất thực nghiệm xuất hiện mặt N khi tung đồng xu 20 lần là
Số lần xuất hiện mặt N là: 11:20 = \(\frac{11}{20}\)
Xác suất thực nghiệm xuất hiện mặt S khi tung đồng xu 20 lần là
Số lần xuất hiện mặt S là: 9:20 = \(\frac{9}{20}\)
Bài 2 trang 19 SGK Toán 6 tập 2 - Cánh Diều
Trả lời các câu hỏi sau:
a) Nếu tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
b) Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
c) Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
Phương pháp:
*Xác suất thực nghiệm xuất hiện mặt N bằng
Số lần xuất hiện mặt N : Tổng số lần tung đồng xu
*Xác suất thực nghiệm xuất hiện mặt S bằng
Số lần xuất hiện mặt S : Tổng số lần tung đồng xu
Lời giải:
a) Nếu tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng: \(\frac{13}{22}\)
b) Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng: \(\frac{11}{25}\)
c) Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất hiện mặt N thì 30−14=16 lần xuất hiện mặt S. Xác suất thực nghiệm xuất hiện mặt S bằng:
\(\frac{16}{30}\)= \(\frac{8}{15}\)
Bài 3 trang 20 SGK Toán 6 tập 2 - Cánh Diều
Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3,..., 10; hai thẻ khác nhau thì ghi hai số khác nhau.
Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
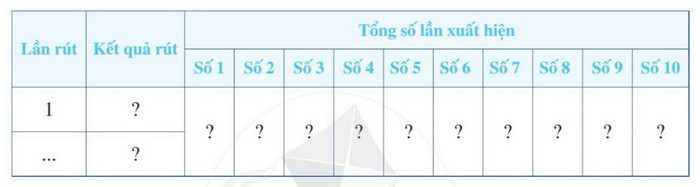
Tính xác suất thực nghiệm:
a)Xuất hiện số 1;
b ) Xuất hiện số 5;
c)Xuất hiện số 10;
Phương pháp:
*Xác suất thực nghiệm xuất hiện số A bằng
Số lần xuất hiện số A : Tổng số lần rút thẻ
Lời giải:
Sau 25 lần rút thẻ liên tiếp, ta được kết quả thống kê sau:
|
Lần rút |
Kết quả rút |
Tổng số lần xuất hiện |
|||||||||
|
Số 1 |
Số 2 |
Số 3 |
Số 4 |
Số 5 |
Số 6 |
Số 7 |
Số 8 |
Số 9 |
Số 10 |
||
|
1 |
2 |
1 |
4 |
2 |
2 |
4 |
3 |
3 |
2 |
2 |
2 |
|
2 |
5 |
||||||||||
|
3 |
6 |
||||||||||
|
4 |
10 |
||||||||||
|
5 |
3 |
||||||||||
|
6 |
5 |
||||||||||
|
7 |
7 |
||||||||||
|
8 |
2 |
||||||||||
|
9 |
4 |
||||||||||
|
10 |
4 |
||||||||||
|
11 |
6 |
||||||||||
|
12 |
9 |
||||||||||
|
13 |
5 |
||||||||||
|
14 |
1 |
||||||||||
|
15 |
7 |
||||||||||
|
16 |
8 |
||||||||||
|
17 |
2 |
||||||||||
|
18 |
10 |
||||||||||
|
19 |
2 |
||||||||||
|
20 |
3 |
||||||||||
|
21 |
5 |
||||||||||
|
22 |
8 |
||||||||||
|
23 |
6 |
||||||||||
|
24 |
7 |
||||||||||
|
25 |
9 |
||||||||||
a) Xác suất thực nghiệm xuất hiện số 1 là: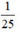
b) Xác suất thực nghiệm xuất hiện số 5 là: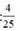
c) Xác suất thực nghiệm xuất hiện số 10 là: 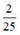
Bài 4 trang 20 SGK Toán 6 tập 2 - Cánh Diều
Gieo một xúc xắc 10 lần liên tiếp, bạn Cường có kết quả như sau:
a) Hãy kiểm đếm số lần xuất hiện mặt 1 chấm và số lần xuất hiện mặt 6 chấm sau 10 lần gieo. Xác suất thực nghiệm xuất hiện
b) Tính xác suất thực nghiệm xuất hiện mặt 1 chấm.
c) Tính xác suất thực nghiệm xuất hiện mặt 6 chấm.
Phương pháp:
Đếm số lần xuất hiện các mặt
*Xác suất thực nghiệm xuất hiện mặt X bằng
Số lần xuất hiện mặt X : Tổng số lần gieo xúc xắc
Lời giải:
a) Số lần xuất hiện mặt 1 chấm: 3 lần
Số lần xuất hiện mặt 6 chấm: 1 lần
b) Xác suất thực nghiệm xuất hiện mặt 1 chấm là: \(\frac{3}{10}\)
c) Xác suất thực nghiệm xuất hiện mặt 6 chấm là: \(\frac{1}{10}\)
Bài 5 trang 20 SGK Toán 6 tập 2 - Cánh Diều
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
Phương pháp:
*Xác suất thực nghiệm xuất hiện mặt X bằng
Số lần xuất hiện mặt X : Tổng số lần gieo xúc xắc
Lời giải:
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng: \(\frac{5}{11}\)
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng: \(\frac{3}{14}\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4 trang 104, 105, 106 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 trang 102, 103 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 92, 93 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6 trang 87, 88 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Giải bài 1, 2, 3, 4, 5, 6 trang 83 SGK Toán 6 tập 2 Cánh Diều (10/10)
- Hoạt động thực hành và trải nghiệm chủ đề 3. Sắp xếp các vị trí thẳng hàng
- Bài tập cuối chương 6
- Bài 5. Góc
- Bài 4. Tia
- Bài 3. Đoạn thẳng
- Bài 2. Hai đường thẳng cắt nhau. Hai đường thẳng song song
- Bài 1. Điểm. Đường thẳng
- Chương 6. Hình học phẳng
- Hoạt động thực hành và trải nghiệm. Chủ đề 2. Chỉ số khối cơ thể (BMI)
- Bài tập cuối chương 5
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
