Giải bài 1, 2, 3, 4 trang 92 SGK Toán 9 Cánh Diều tập 1

Bài 1 trang 92 SGK Toán 9 tập 1 - Cánh Diều

Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \) (Hình 40).

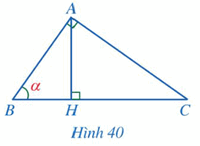
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng:

A. \(\sin \alpha \).

B. \(\cos \alpha \).

C. \(\tan \alpha \).

D. \(\cot \alpha \).

b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng:

A. \(\sin \alpha \).

B. \(\cos \alpha \).

C. \(\tan \alpha \).

D. \(\cot \alpha \).

c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng:

A. \(\sin \alpha \).

B. \(\cos \alpha \).

C. \(\tan \alpha \).

D. \(\cot \alpha \).

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

a) Đáp án đúng là: C

Xét ∆ABH vuông tại H, ta có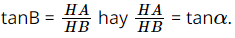 

b) Đáp án đúng là: D

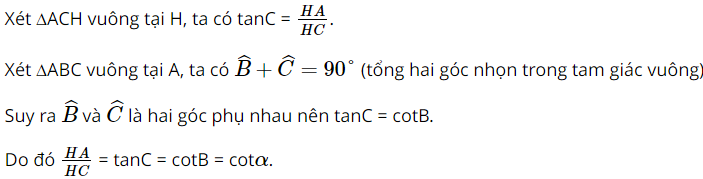
c) Đáp án đúng là: B

Bài 2 trang 92 SGK Toán 9 tập 1 - Cánh Diều

Cho hình thoi \(ABCD\) có \(AB = a,\widehat {BAD} = 2\alpha \left( {0^\circ  < \alpha  < 90^\circ } \right)\). Chứng minh:

a) \(BD = 2a.\sin \alpha \).

b) \(AC = 2a.\cos \alpha \).

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

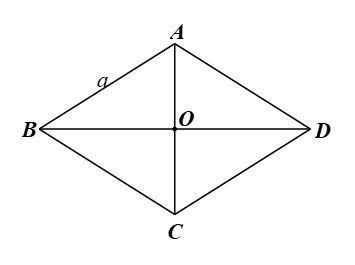
a) Gọi O là giao điểm của đường chéo AC và BD.

Vì ABCD là hình thoi nên AC ⊥ BD tại trung điểm O của mỗi đường và AC là đường phân giác của 

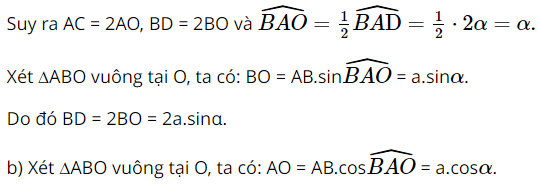
Do đó AC = 2AO = 2a.cosα.

Bài 3 trang 92 SGK Toán 9 tập 1 - Cánh Diều

Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) \(OA = 3m\) tạo với phương thẳng đứng một góc là \(\widehat {AOH} = 43^\circ \) thì khoảng cách \(AH\) từ em bé đến vị trí cân bằng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Xét ∆OAH vuông tại H, ta có: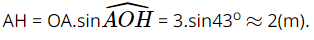 

Vậy khoảng cách từ em bé đến vị trí cân bằng khoảng 2 m.

Bài 4 trang 92 SGK Toán 9 tập 1 - Cánh Diều

Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:

- Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ \).

- Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ \); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ \) (Hình 42).

Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).

Phương pháp:

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải:

Kẻ AA’ (A’ ∈ BC) theo phương Bắc – Nam và kẻ BB’, CC’ theo phương Nam – Bắc (hình vẽ). Khi đó AA’ // BB’ // CC’.

Phương BA lệch với phương Nam – Bắc về hướng Đông 52° nên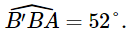 

Phương CA lệch với phương Nam – Bắc về hướng Tây 27° nên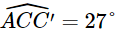 

Phương CB lệch với phương Nam – Bắc về hướng Tây 70° nên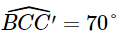 

Do đó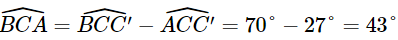  

Kẻ BH ⊥ AC (H ∈ AC).

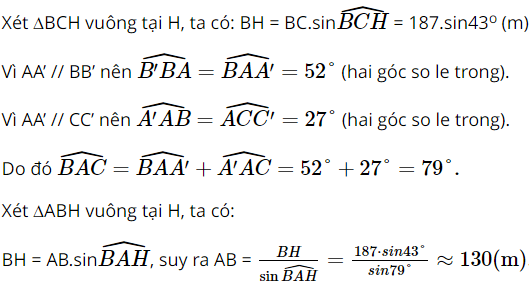
Vậy khoảng cách AB khoảng 130 mét.

Sachbaitap.com