Giải bài 3.9, 3.10, 3.11, 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, 3.18 trang 66 SGK Toán 6 Kết nối tri thức tập 1

Bài 3.9 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Tính tổng hai số cùng dấu:

a) (-7) + (-2);             b) (-8) + (-5):

c) (-11) + (-7);           d) (-6) + (-15).

Phương pháp:

Muốn cộng hai số nguyên âm, ta công phần số tự nhiên của chúng với nhau rồi đặt dấu "-" trước kết quả.

Lời giải:

a) (-7) + (-2) = -(7 + 2) = -9

b) (-8) + (-5) = -(8 + 5) = -13

c) (-11) + (-7) = -( 11 + 7) = -18

d) (-6) + (-15) = -(6 + 15) = -21

Bài 3.10 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Tính tổng hai số khác dấu:

a) 6 + (-2);                b) 9 + (-3);

c) (-10) + 4               d) (-1) + 8.

Phương pháp:

Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.

Lời giải:

a) 6 + (-2) = 6 – 2 = 4

b) 9 + (-3) = 9 – 3 = 6

c) (-10) + 4 = -(10 – 4) = -6

d) (-1) + 8 = 8 – 1 = 7

Bài 3.11 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Biểu diễn - 4 và số đối của nó trên cùng một trục số.

Phương pháp:

Trên trục số hai điểm có cùng khoảng cách đến gốc O được gọi là hai số đối nhau.

Lời giải:

Số đối của 4 là - 4. Ta biểu diễn chúng trên trục số:

Bài 3.12 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Thực hiện các phép trừ sau:

a) 9 - (-2);

b) (-7) - 4

c) 27 - 30

d) (-63) - (-15).

Phương pháp:

Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: a - b = a + (-b).

Lời giải:

a) 9 – (-2) = 9 + 2 = 11

b) ) (-7) – 4 = (-7) + (-4) = - (7 + 4) = -11

c) 27 – 30 = 27 + (- 30) = - (30 – 27) (do 30 > 27) = - 3

d) (-63) – ( -15)  = (- 63) + 15 = - (63 – 15) (do 63 > 15) = - 48

Bài 3.13 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Hai ca nô cùng xuất phát từ C đi về phía A hoặc B như hình vẽ. Ta quy ước chiều từ C đến B là chiều dương ( nghĩa là vận tốc và quãng đường đi từ C về phía B được biểu thị bằng số dương và theo chiều ngược lại là số âm). Hỏi sau một giờ, hai ca nô cách nhau bao nhiêu kilomet nếu vận tốc của chúng lần lượt là:

a) 11 km/h và 6 km/h

b) 11 km/h và -6 km/h

Phương pháp:

Vận tốc âm tức là cano đi theo chiều âm

Số km đi trong 1 giờ chính là vận tốc

Lời giải:

Quãng đường ca nô 1 đi được trong 1 giờ là: 11 . 1 = 11 (km)

Quãng đường ca nô 2 đi được trong 1 giờ là: 6 . 1 = 6 (km)

a) Do 2 ca nô đi cùng chiều nên khoảng cách của 2 ca nô là hiệu quãng đường đi được

Sau một giờ, hai ca nô cách nhau số kilomet là:

11 - 6 = 5 (km)

b) Vì 2 vận tốc trái dấu, tức là 2 ca nô đi ngược chiều nên khoảng cách của 2 ca nô là tổng quãng đường đi được

Sau một giờ, hai ca nô cách nhau số kilomet là:

11 + 6 = 17 (km)

Bài 3.14 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Mỗi hình sau đây mô phỏng phép tính nào? (Tất cả đều xuất phát từ gốc O).

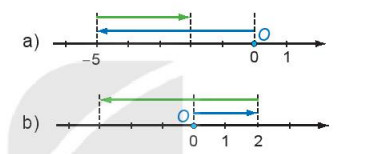
Phương pháp:

Khi di chuyển chiều sang phải trục số ta thực hiện phép cộng, di chuyển sang trái ta thực hiện phép trừ.

Lời giải:

a) Hình mô phỏng phép tính: (-5) + 3 hoặc (-5) - (- 3);

b) Hình mô phỏng phép tính: 2 – 5 hoặc 2 + (-5).

Bài 3.15 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Tính một cách hợp lí:

a) 152 + (-73) - (-18) - 127;

b) 7 + 8+ (-9) + (-10).

Phương pháp:

Áp dụng tính chất giao hoán và phân phối của phép cộng

Lời giải:

a) 152 + (-73) - (-18) - 127 = 152 – 73 +18 -127

= (152 + 18) – (127 + 73) = 170 - 200 = -(200 - 170) = -30

b) 7 + 8 + (-9)  + (-10) = (7 + 8) + [(-9)  + (-10)]

= 15 + (-19) = -(19 - 15)= -4.

Bài 3.16 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Tính một cách hợp lí:

a) 152 + (-73) - (-18) - 127;

b) 7 + 8+ (-9) + (-10).

Phương pháp:

Áp dụng tính chất giao hoán và phân phối của phép cộng

Lời giải:

a) 152 + (-73) - (-18) - 127 = 152 – 73 +18 -127

= (152 + 18) – (127 + 73) = 170 - 200 = -(200 - 170) = -30

b) 7 + 8 + (-9)  + (-10) = (7 + 8) + [(-9)  + (-10)]

= 15 + (-19) = -(19 - 15)= -4.

Bài 3.17 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Tính giá trị của biểu thức (-156) - x, khi:

a) x = -26

b) x  = 76

c) x = (-28) - (-143)

Phương pháp:

- Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu "-" trước kết quả.

- Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phần số tự nhiên của chúng ( số lớn trừ số bé) rồi đặt trước kết quả tìm được dấu của số có phần số tự nhiên lớn hơn.

- Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: a - b = a + (-b).

Lời giải:

a) Thay x = -26 vào biểu thức (-156) - x ta được:

(-156) – x = (-156) – (-26) = (-156) + 26 = - (156 – 26) = - 130. (do 156 > 26)

b) Thay x = 76 vào biểu thức (-156) - x ta được:

(-156) – x = (-156) – 76 = (-156) + (-76) = - (156 + 76) = - 232.

c) Thay x = (- 28) – (- 143) vào biểu thức (-156) - x ta được:

(-156) – x = (-156) – [(-28) – (-143)] = (-156) – [(-28) + 143] = (-156) – (143 – 28) 

= (- 156) – 115 = (-156) + (-115) = - (156 + 115) = - 271.

Bài 3.18 trang 66 SGK Toán 6 tập 1 - Kết nối tri thức

Câu hỏi: 

Thay mỗi dấu "*" bằng một chữ số thích hợp để có:

a) (\( - \overline {6*} \)) + (-34) =  - 100;

b) (-789) + \(\overline {2**} \) = -515.

Lời giải:

a) (\( - \overline {6*} \)) + (-34) =  - 100

    (\( - \overline {6*} \)) = -100 – (-34)

    (\( - \overline {6*} \))  = -100 + 34

     (\( - \overline {6*} \)) = -66

Vậy dấu * là chữ số 6.

b) (-789) + \(\overline {2**} \) = -515.

\(\overline {2**} \) = -515 - (-789)

\(\overline {2**} \) = -515 + 789

\(\overline {2**} \) = 274

Vậy hai dấu * lần lượt là 7 và 4.

Sachbaitap.com