Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1
Giải SGK Toán 9 trang 103 Kết nối tri thức tập 1. Bài 5.21: Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại điểm A.
Bài 5.20 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?
Phương pháp:
So sánh bán kính của mỗi hình tròn với khoảng cách giữa 2 đường thẳng, nếu hình tròn có bán kính lớn hơn thì nó đè lên đường thẳng a, ngược lại thì hình tròn không đè lên đường thẳng a.
Lời giải:
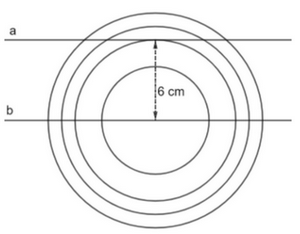
Vì a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm nên đường thẳng a tiếp xúc với hình tròn bán kính 6 cm, hay hình tròn bán kính 6 cm đè lên đường thẳng a.
Vì 4 cm < 6 cm nên đường thẳng a và hình tròn bán kính 4 cm không cắt nhau, hay hình tròn bán kính 4 cm không đè lên trường thẳng a.
Vì 7 cm > 6 cm; 8 cm > 6 cm nên đường thẳng a và hình tròn bán kính 4 cm cắt nhau, hay hình tròn bán kính 7 cm và 8 cm đè lên đường thẳng a.
Vậy hình tròn bán kính 4 cm không đè lên trường thẳng a, hình tròn bán kính 6 cm, 7 cm và 8 cm đè lên đường thẳng a.
Bài 5.21 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Chứng minh đường thẳng đi qua A là và song song với BC là tiếp tuyến tức là đường thẳng đó vuông góc với bán kính (hoặc đường kính) tại điểm A.
Phương pháp:
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Lời giải:
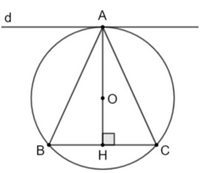
Ta có đường thẳng AO là trục đối xứng của đường tròn.
Nên B là điểm đối xứng của C qua AO.
Gọi H là giao điểm của AO và BC.
Khi đó ta có: AH ⊥ BC mà d // BC nên AH ⊥ d.
Vậy d là một tiếp tuyến của đường tròn.
Bài 5.22 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại P. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (P; PA).
Phương pháp:
Ta có: OA là tiếp tuyến của đường tròn (P; PA) do OA \( \bot \) PA tại A.
Xét cặp tam giác OAP và tam giác OBP, từ đó suy ra PA = PB và OB \( \bot \) PB. Hay OB là tiếp tuyến của đường tròn (P; PA).
Lời giải:
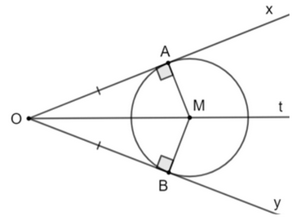
Xét ΔOAM và ΔOBM có:
OM chung

OA = OB
Do đó ΔOAM = ΔOBM (c.g.c).
Suy ra AM = BM (hai cạnh tương ứng).
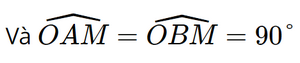 (hai góc tương ứng) hay OB ⊥ MB.
(hai góc tương ứng) hay OB ⊥ MB.
Do đó OA là tiếp tuyến của đường tròn (M; MA).
Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).
Bài 5.23 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Phương pháp:
Áp dụng tính chất của hai tiếp tuyến cắt nhau.
Lời giải:
a)
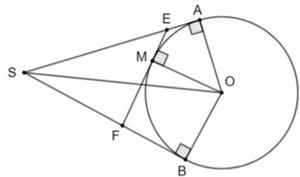
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA.
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB.
Chu vi tam giác SEF là:
CSEF = SE + SF + EF = SE + SF + EM + MF
= SE + EA + SF + BF = SA + SB.
Vậy chu vi của tam giác SEF bằng SA + SB.
b)
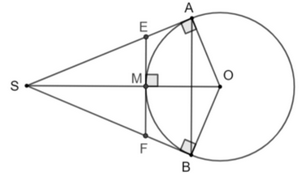
Vì SA và SB là hai tiếp tuyến cắt nhau tại S nên SO là phân giác của .
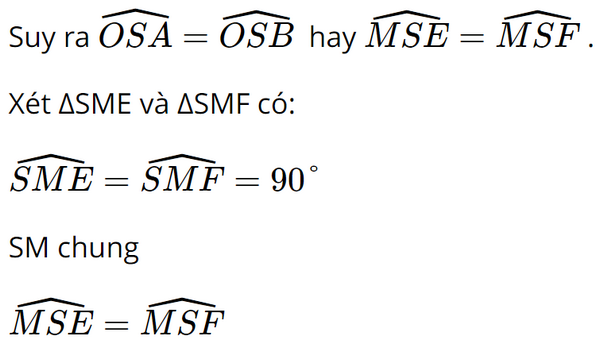
Do đó ΔSME = ΔSMF (g.c.g)
Suy ra SE = SF (hai cạnh tương ứng).
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 114, 115 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.32, 5.33, 5.34, 5.35, 5.36, 5.37, 5.38, 5.39, 5.40 trang 113 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.28, 5.29, 5.30, 5.31 trang 110 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.24, 5.26, 5.27 trang 107 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Giải bài 5.20, 5.21, 5.22, 5.23 trang 103 SGK Toán 9 Kết nối tri thức tập 1 (10/09)
- Pha chế dung dịch theo nồng độ yêu cầu
- Bài tập cuối chương 5
- Luyện tập chung trang 108
- Bài 17: Vị trí tương đối của hai đường tròn
- Bài 16: Vị trí tương đối của đường thẳng và đường tròn
- Luyện tập chung trang 96
- Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Bài 14: Cung và dây của một đường tròn
- Bài 13: Mở đầu về đường tròn
- Chương V: Đường tròn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
