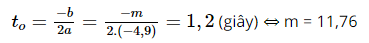Giải SBT Toán 10 trang 13, 14, 15 Kết nối tri thức tập 2

Bài 6.11 trang 13 SBT Toán 10 tập 2 Kết nối tri thức

Cho đồ thị của hai hàm số bậc hai như dưới đây

Với mỗi đồ thị, hãy:

a) Tìm tọa độ đỉnh của đồ thị

b) Tìm khoảng đồng biến và khoảng nghịch biến của hàm số

c) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số

d) Tìm tập xác định và tập giá trị của hàm số

Phương pháp:

Dựa vào đồ thị, xác định các giá trị: tọa độ đỉnh, sự biến thiên, các khoảng giá trị của x và y để tìm các giá trị tương ứng theo yêu cầu đề bài

Lời giải:

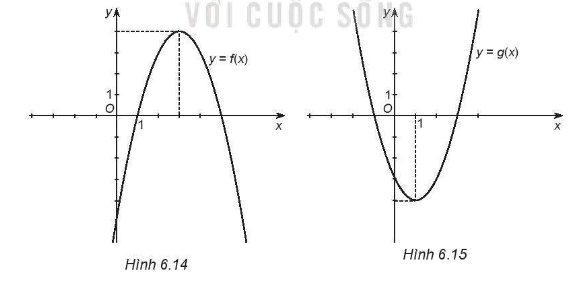
a) Xét Hình 6.14

+) Đồ thị hàm số có đỉnh \({I_1}(3;4)\)

+) Hàm số đồng biến trên \(( - \infty ;3)\) và nghịch biến trên \((3; + \infty )\)

+) Hàm số có giá trị lớn nhất là 4, đạt được khi x = 3

+) Hàm số có tập xác định là \(\mathbb{R}\) và tập giá trị là \({\rm{( - }}\infty {\rm{;4]}}\)

b) Xét Hình 6.15

+) Đồ thị hàm số có đỉnh \({I_2}(1; - 4)\)

+) Hàm số nghịch biến trên \(( - \infty ;1)\) và đồng biến trên \((1; + \infty )\)

+) Hàm số có giá trị nhỏ nhất là -4, đạt được khi x = 1

+) Hàm số có tập xác định là \(\mathbb{R}\) và tập giá trị là \({\rm{[}} - 4; + \infty )\)

Bài 6.12 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

Với mỗi hàm số bậc hai cho dưới đây: \(y = f(x) =  - {x^2} - x + 1\);  \(y = g(x) = {x^2} - 8x + 8\)

Hãy thực hiện các yêu cầu sau:

a) Viết lại hàm số bậc hai dưới dạng \(y = a{(x - h)^2} + k\)

b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số

c) Vẽ đồ thị của hàm số

Lời giải:

a) Ta có:

\(y = f(x) =  - {x^2} - x + 1 \Leftrightarrow f(x) =  - \left( {{x^2} + x + \frac{1}{4}} \right) + \frac{5}{4} \Leftrightarrow f(x) =  - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4}\)

\(y = g(x) = {x^2} - 8x + 8 \Leftrightarrow g(x) = {x^2} - 8x + 16 - 8 \Leftrightarrow g(x) = {(x - 4)^2} - 8\)

b) Ta có:

\(f(x) =  - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4} \le \frac{5}{4}\) \( \Rightarrow \) GTLN của f(x) là \(\frac{5}{4}\) đạt được khi \(x =  - \frac{1}{2}\)

\(g(x) = {(x - 4)^2} - 8 \ge  - 8 \Rightarrow \) GTNN của g(x) là -8 đạt được khi x = 4

c)

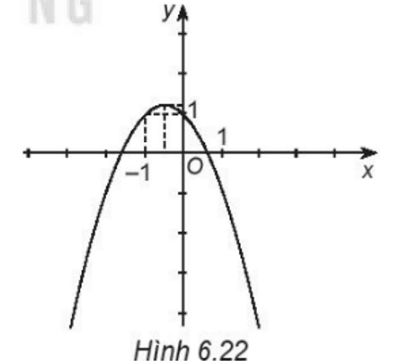
- Đồ thị hàm số \(y =  - {x^2} - x + 1\) là đường parabol có a = -1 < 0 nên có bề lõm quay xuống dưới.

Đỉnh \(I\left( { - \frac{1}{2};\frac{5}{4}} \right)\), trục đối xứng x = \( - \frac{1}{2}\). Giao điểm của parabol với

trục Oy là điểm (0 ; 1) và cắt trục Ox tại 2 điểm có hoành độ \(x = \frac{{ - 1 - \sqrt 5 }}{2}\) và \(x = \frac{{ - 1 + \sqrt 5 }}{2}\)

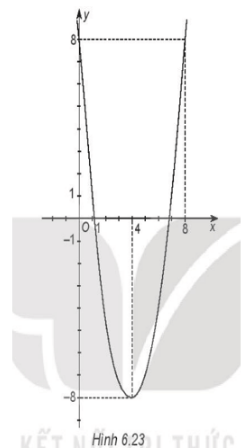
- Đồ thị hàm số \(y = {x^2} - 8x + 8\) là đường parabol có a = 1 > 0 nên có bề lõm quay lên trên

Đỉnh \(I(4; - 8)\), trục đối xứng x = 4. Giao điểm của parabol với trục Oy là điểm (0 ; 8) và cắt trục Ox tại 2 điểm có hoành độ \(x = 4 - 2\sqrt 2 \) và \(x = 4 + 2\sqrt 2 \)

Bài 6.13 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

Tìm tập xác định và tập giá trị của các hàm số bậc hai sau:

a) \(f(x) =  - {x^2} + 4x - 3\)   

b) \(f(x) = {x^2} - 7x + 12\)

Lời giải:

a) Hàm số \(f(x) =  - {x^2} + 4x - 3\) có tập xác định là D = \(\mathbb{R}\)

Do a = -1 < 0, ∆ = 4 nên hàm số \(f(x) =  - {x^2} + 4x - 3\) có tập giá trị là \(\left( { - \infty ;1} \right]\)

b) Hàm số \(f(x) = {x^2} - 7x + 12\) có tập xác định là D = \(\mathbb{R}\)

Do a = 1 > 0, ∆ = 1 nên hàm số \(f(x) = {x^2} - 7x + 12\)có tập giá trị là \(\left[ { - \frac{1}{4}; + \infty } \right)\)

Bài 6.14 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

Tìm parabol \(y = a{x^2} + bx + 2\), biết rằng parabol đó

a) Đi qua hai điểm \(M(1;5)\) và \(N( - 2;8)\)

b) Đi qua điểm \(A(3; - 4)\) và có trục đối xứng \(x =  - \frac{3}{2}\)

c) Có đỉnh \(I(2; - 2)\)

Lời giải:

a) Thay tọa độ điểm \(M(1;5)\) và \(N( - 2;8)\) vào hàm số ta có hệ PT:

\(\left\{ \begin{array}{l}5 = a + b + 2\\8 = 4a - 2b + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b = 3\\4a - 2b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\end{array} \right.\)

Vậy hàm số có dạng \(y = 2{x^2} + x + 2\)

b) Thay tọa độ điểm \(A(3; - 4)\) ta có PT: \(9a + 3b + 2 =  - 4 \Leftrightarrow 3a + b =  - 2\)

Parabol có trục đối xứng \(x =  - \frac{3}{2}\) \( \Rightarrow \) \( - \frac{b}{{2a}} =  - \frac{3}{2} \Leftrightarrow 3a - b = 0\)

Khi đó ta có hệ PT: \(\left\{ \begin{array}{l}3a + b =  - 2\\3a - b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \frac{1}{3}\\b =  - 1\end{array} \right.\)

Vậy hàm số có dạng \(y =  - \frac{1}{3}{x^2} - x + 2\)

c) Parabol có đỉnh \(I(2; - 2)\) \( \Rightarrow  - \frac{b}{{2a}} = 2 \Leftrightarrow 4a + b = 0\)

Thay tọa độ đỉnh \(I(2; - 2)\) vào hàm số ta có PT: \(4a + 2b + 2 =  - 2 \Leftrightarrow 2a + b =  - 2\)

Khi đó ta có hệ PT: \(\left\{ \begin{array}{l}4a + b = 0\\2a + b =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 4\end{array} \right.\)

Vậy hàm số có dạng: \(y = {x^2} - 4x + 2\)

Bài 6.15 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

Tìm phương trình của parabol có đỉnh \(I( - 1;2)\) và đi qua điểm \(A(1;6)\)

Lời giải:

Gọi parabol cần tìm có dạng là \(y = a{x^2} + bx + c(a \ne 0)\)

Thay tọa độ điểm \(A(1;6)\) và đỉnh \(I( - 1;2)\) vào hàm số ta có các PT: \(a + b + c = 6\) và \(a - b + c = 2\)

Parabol có đỉnh \(I( - 1;2)\) \( \Rightarrow  - \frac{b}{{2a}} =  - 1 \Leftrightarrow 2a - b = 0\)

Khi đó ta có hệ PT: \(\left\{ \begin{array}{l}a + b + c = 6\\a - b + c = 2\\2a - b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 3\end{array} \right.\)

Vậy parabol đó là \(y = {x^2} + 2x + 3\)

Bài 6.16 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

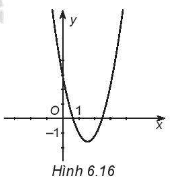
Xác định dấu của các hệ số a, b, c và dấu của biệt thức \(\Delta  = {b^2} - 4ac\) của hàm số bậc hai \(y = a{x^2} + bx + c\), biết đồ thị của nó có dạng như Hình 6.16.

Phương pháp:

Bước 1: Dựa vào chiều bề lõm quay lên trên/ xuống dưới để tìm dấu của hệ số a

Bước 2: Xét dấu của tung độ giao điểm của ĐTHS với trục Oy để tìm dấu của hệ số c

Bước 3:  Xét dấu tọa độ đỉnh của parabol để xét dấu các biểu thức  \( - \frac{b}{{2a}}\) và \( - \frac{\Delta }{{4a}}\). Từ đó suy ra dấu của hệ số b và ∆

Lời giải:

Từ đồ thị của hàm số ta thấy:

+ Đồ thị quay bề lõm quay lên trên nên a > 0.

+ Đồ thị cắt trục tung tại điểm có tung độ dương nên ta có: a.0² + b.0 + c > 0 ⇔ c > 0.

+ Hoành độ đỉnh -b²a có giá trị dương nên a và b trái dấu. Vì a > 0 nên b < 0.

+ Mặt khác, vì đồ thị hàm số cắt trục hoành Ox tại hai điểm phân biệt, tức là phương trình ax² + bx + c = 0 có hai nghiệm phân biệt nên ∆ = b² – 4ac > 0.

Vậy a > 0, b < 0, c > 0 và ∆ = b² – 4ac > 0.

Bài 6.17 trang 14 SBT Toán 10 tập 2 Kết nối tri thức

Bác Hùng dùng 200 m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.

a) Tìm công thức tính diện tích S(x) của mảnh vườn hình chữ nhật rào được theo chiều rộng x (m) của mảnh vườn đó

b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.

Lời giải:

a) Theo giả thiết, chu vi mảnh đất hình chữ nhật là 200 m  \( \Rightarrow \) Nửa chu vi hình chữ nhật là 100 m

Gọi x (m) (0 < x < 100) là chiều rộng mảnh vườn hình chữ nhật

\( \Rightarrow \) Chiều dài mảnh vườn hình chữ nhật là 100 – x (m)

Khi đó diện tích mảnh vườn hình chữ nhật là: \(S(x) = x(100 - x) \Leftrightarrow S(x) =  - {x^2} + 100x\) (m²)

b) Ta có: \(S(x) =  - {x^2} + 100x =  - ({x^2} - 100x + 2500) + 2500 =  - {(x - 50)^2} + 2500 \le 2500\)

\( \Rightarrow \) S(x) đạt GTLN là 2 500 khi x = 50

Vậy với kích thước hình chữ nhật là 50 x 50 (m) (rào mảnh vườn thành hình vuông) thì diện tích mảnh vườn lớn nhất.

Bài 6.18 trang 15 SBT Toán 10 tập 2 Kết nối tri thức

Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu 14,7 m/s. Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) có thể mô tả bởi PT:

\(h(t) =  - 4,9{t^2} + 14,7t\)

a) Sau khi ném bao nhiêu giây thì quả bóng đạt độ cao lớn nhất?

b) Tìm độ cao lớn nhất của quả bóng

c) Sau khi ném bao nhiêu giây thì quả bóng rơi chạm đất?

Lời giải:

a) Quả bóng đạt độ cao lớn nhất tại điểm đỉnh của parabol \(h(t) =  - 4,9{t^2} + 14,7t\), trong đó thời gian để đạt độ cao lớn nhất là hoành độ của đỉnh.

Hàm số \(y =  - 4,9{x^2} + 14,7x\) có hoành độ đỉnh \(I\) là \(x =-\frac{14,7}{2.(-4,9)}= \frac{3}{2}\)

Vậy sau 1,5 giây thì quả bóng đạt độ cao lớn nhất.

b) Độ cao lớn nhất của quả bóng là tung độ đỉnh của parabol \(h(t) =  - 4,9{t^2} + 14,7t\), là độ cao đạt được sau1,5 giây

Độ cao đó là: \(h(1,5) =  - 4,9{1,5^2} + 14,7.1,5=\frac{441}{40}=11,025\)

c) Quả bóng chạm đất tức là độ cao của nó bằng 0.

Giải PT: h(t) = 0 \( \Leftrightarrow  - 4,9{t^2} + 14,7t = 0 \Leftrightarrow t = 0\) hoặc \(t=3\)

(t=0 tức là khi chưa ném.)

Vậy sau 3 giây thì quả bóng rơi chạm đất.

Bài 6.19 trang 15 SBT Toán 10 tập 2 Kết nối tri thức

Một hòn đá được ném lên trên theo phương thẳng đứng. Khi bỏ qua sức cản của không khí, chuyển động của hòn đá tuân theo phương trình sau:

\(y =  - 4,9{t^2} + mt + n\)

với m, n là các hằng số. Ở đây t = 0 là thời điểm hòn đá được ném lên, y(t) là độ cao của hòn đá tại thời điểm t (giây) sau khi ném và y = 0 ứng với bóng chạm đất. 

a) Tìm phương trình chuyển động của hòn đá, biết rằng điểm ném cách mặt đất 1,5 m và thời gian để hòn đá đạt độ cao lớn nhất là 1,2 giây sau khi ném

b) Tìm độ cao của hòn đá sau 2 giây kể từ khi bắt đầu ném

c) Sau bao lâu kể từ khi ném, hòn đá rơi xuống mặt đất (Kết quả làm tròn đến chữ số thập phân thứ hai)?

Lời giải:

a)

Theo giả thiết điểm ném ở độ cao 1,5 m so với mặt đất nên n = 1,5.

Công thức tính độ cao của quả bóng so với mặt đất (tính bằng mét) có thể mô tả bởi phương trình y = –4,9t² + mt + 1,5 là một hàm số bậc hai có a = –4,9 < 0 có đồ thị là một parabol có bề lõm hướng xuống, do đó, quả bóng đạt độ cao lớn nhất là tung độ của đỉnh parabol tại thời gian ứng với hoành độ đỉnh của parabol là:

Vậy phương trình chuyển động của hòn đá là: y = –4,9t² + 11,76t + 1,5.

b)

Khi t = 2 ta có y = –4,9. 2² + 11,76. 2 + 15 = 5,42.

Vậy sau 2 giây, hòn đá có độ cao là 5,42 m.

c)

Hòn đá rơi xuống mặt đất tức là y = 0. Xét phương trình

–4,9t² + 11,76t + 15 = 0 ⇔ t ≈ 2,52 hoặc t ≈ –0,12 (loại).

Vậy sau khoảng 2,52 giây kể từ khi ném thì hòn đá rơi xuống mặt đất.

Bài 6.20 trang 15 SBT Toán 10 tập 2 Kết nối tri thức

Một rạp chiếu phim có sức chứa 1 000 người. Với giá vé là 40 000 đồng, trung bình sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã kháo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng thì sẽ có thêm 100 người đến xem phim mỗi ngày.

a) Tìm công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé mỗi ngày của rạp chiếu phim khi giá vé là x nghìn đồng

b) Tìm mức giá vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.

Lời giải:

a) Ta có: Với giá vé là x nghìn đồng thì số tiền giảm giá so với giá vé cũ là 40 – x (nghìn đồng)

Số người tăng lên sau khi giảm giá vé là: \(\frac{{40 - x}}{{10}}.100 = 400 - 10x\)

Số người đến rạp mỗi ngày sau khi giảm giá là: \(300 + 400 - 10x = 700 - 10x\)

\( \Rightarrow \) Doanh thu từ tiền bán vé mỗi ngày của rạp là: \(R(x) = x(700 - 10x) =  - 10{x^2} + 700x\) (nghìn đồng)

b) Hàm số \(R(x) =  - 10{x^2} + 700x\) đạt giá trị lớn nhất tại \(x =  - \frac{b}{{2a}} = 35\)

Vậy với giá vé 35 nghìn đồng thì doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.

Sachbaitap.com