Giải SGK Toán 11 Cánh Diều tập 2 trang 24

Bài 1 trang 24 SGK Toán 11 - Cánh Diều tập 2

Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:

A: “Lần thứ nhất xuất hiện mặt ngửa”;

B: “Lần thứ hai xuất hiện mặt ngửa”;

C: “Cả hai lần đều xuất hiện mặt ngửa”;

D: “Có ít nhất một lần xuất hiên mặt ngửa”.

Trong hai biến cố C, D, biến cố nào là biến cố hợp của hai biến cố A, B? Biến cố nào là biến cố giao của hai biến cố A, B?

Phương pháp:

- Xác định số trường hợp xảy ra của từng biến cố

- Rồi xác định giao, hợp của hai biến cố A, B

Lời giải:

⦁ Biến cố hợp của hai biến cố A và B là biến cố mà lần thứ nhất hoặc lần thứ hai tung đồng xu xuất hiện mặt ngửa, tức là “Có ít nhất một lần xuất hiện mặt ngửa”. Vậy biến cố D là biến cố hợp của A và B.

⦁ Biến cố giao của hai biến cố A và B là biến cố mà cả hai lần đều xuất hiện mặt ngửa. Do đó biến cố C: “Cả hai lần đều xuất hiện mặt ngửa” là biến cố hợp của A và B.

Bài 2 trang 24 SGK Toán 11 - Cánh Diều tập 2

Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:

A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 4”;

B: “Số chấm xuất hiện ở lần gieo thứ hai nhỏ hơn 4”;

C: “Số chấm xuất hiện ở lần gieo thứ nhất nhỏ hơn 4”;

Trong các biến cố trên, hãy:

a) Tìm cặp biến cố xung khắc;

b) Tìm cặp biến cố độc lập.

Phương pháp:

- Xác định phần tử của từng tập hợp

- Xác định biến cố xung khắc và biến cố độc lập

Lời giải:

a) Cặp biến cố xung khắc là A và C, vì nếu A xảy ra thì C không thể xảy ra, và ngược lại, nếu C xảy ra thì A không thể xảy ra.

b) Cặp biến cố độc lập là A và B, vì xảy ra hay không xảy ra biến cố A không ảnh hưởng đến khả năng xảy ra biến cố B, và ngược lại, xảy ra hay không xảy ra biến cố B cũng không ảnh hưởng đến khả năng xảy ra biến cố A.

Tương tự, các cặp biến cố A và C, B và C cũng là biến cố độc lập.

Vậy các biến cố độc lập là: A và B; A và C; B và C.

Bài 3 trang 24 SGK Toán 11 - Cánh Diều tập 2

Chọn ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của biến cố M: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11 hoặc chia hết cho 12”.

Phương pháp:

- Sử dụng quy tắc chỉnh hợp để tìm ra phần tử của không gian mẫu.

- Sử dụng quy tắc liệt kê để liệt kê các phần tử của tập hợp M.

Lời giải:

Ta có: Ω = {10; 11; 12; …; 99}.

Không gian mẫu của phép thử có 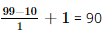phần tử, tức là n(Ω) = 90.

Xét các biến cố:

M: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11 hoặc chia hết cho 12”.

A: “Số tự nhiên có hai chữ số được viết ra chia hết cho 11”;

B: “Số tự nhiên có hai chữ số được viết ra chia hết cho 12”;

Khi đó M = A ∪ B và A ∩ B = ∅

Do hai biến cố A và B xung khắc nên n(M) = n(A ∪ B) = n(A) + n(B).

Số các kết quả thuận lợi cho biến cố A là n(A) = 9.

Số các kết quả thuận lợi cho biến cố B là n(B) = 8.

Số các kết quả thuận lợi cho biến cố M là: n(M) = 9 + 8 = 17.

Suy ra P(M) =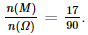 

Bài 4 trang 24 SGK Toán 11 - Cánh Diều tập 2

Một hộp có 12 viên bi có cùng kích thước và khối lượng, trong đó có 7 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi từ hộp đó. Tính xác suất để trong 5 viên bi được chọn có ít nhất 2 viên bi màu vàng.

Phương pháp:

Dùng quy tắc chỉnh hợp để tìm số phần tử của không gian mẫu và tập hợp cần tìm.

Lời giải:

− Mỗi cách chọn ra đồng thời 5 viên bi trong hộp có 12 viên bi cho ta một tổ hợp chập 5 của 12 phần tử. Do đó, không gian mẫu gồm các tổ hợp chập 5 của 12 phần tử và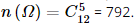 

− Xét biến cố A: “Trong 5 viên bi được chọn có ít nhất 2 viên bi màu vàng”.

Khi đó biến cố đối của biến cố A là 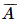 : “Trong 5 viên bi không có viên bi màu vàng hoặc có 1 viên bi màu vàng”.

⦁ Trường hợp 1: Trong 5 viên bi không có viên bi màu vàng.

Có 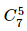= 21 cách chọn.

⦁ Trường hợp 1: Trong 5 viên bi có 1 viên bi màu vàng.

Có 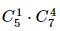= 175 cách chọn.

Như vậy, số kết quả thuận lợi cho biến cố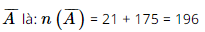 

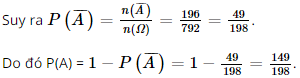
Bài 5 trang 24 SGK Toán 11 - Cánh Diều tập 2

Một hộp có 12 viên bi có cùng kích thước và khối lượng, trong đó có 7 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi từ hộp đó. Tính xác suất để trong 5 viên bi được chọn có ít nhất 2 viên bi màu vàng.

Phương pháp:

Dùng quy tắc chỉnh hợp để tìm số phần tử của không gian mẫu và tập hợp cần tìm

Lời giải:

− Chọn 1 mã đề thi trong 6 mã đề thi môn Toán cho bạn Việt có 6 cách.

Chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh cho bạn Việt có 6 cách.

Chọn 1 mã đề thi trong 6 mã đề thi môn Toán cho bạn Nam có 6 cách.

Chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh cho bạn Nam có 6 cách.

Do đó không gian mẫu của phép thử có số phần tử là 6⁴, tức là n(Ω) = 6⁴.

− Gọi A là biến cố: “Hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó”.

⦁ Trường hợp 1: Hai bạn trùng mã đề thi môn Toán, không trùng mã đề thi môn Tiếng Anh.

Bạn Việt chọn 1 mã đề thi trong 6 mã đề thi môn Toán có 6 cách; chọn 1 mã đề thi trong 6 mã đề thi môn Tiếng Anh có 6 cách.

Bạn Nam chọn 1 mã đề thi môn Toán trùng với mã đề thi bạn Việt đã cho có 1 cách; chọn 1 mã đề thi trong 5 mã đề thi môn Tiếng Anh (trừ mã đề thi bạn Việt đã chọn) có 5 cách.

Như vậy, có 6.6.1.5 = 180 cách.

⦁ Trường hợp 2: Hai bạn trùng mã đề thi môn Tiếng Anh, không trùng mã đề thi môn Toán.

Tương tự trường hợp 1, cũng có 6.1.6.5 = 180 cách.

Như vậy, số kết quả thuận lợi cho biến cố A là: n(A) = 180 + 180 = 360.

Vậy xác suất của biến cố A là:

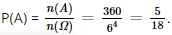
Bài 6 trang 24 SGK Toán 11 - Cánh Diều tập 2

Trong một chiếc hộp có 20 viên bi có cùng kích thước và khối lượng, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh và 5 viên bi màu vàng. Lẫy ngẫu nhiên đồng thời 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có đúng hai màu.

Phương pháp:

-  Dùng các quy tắc đếm để tìm số phần tử của không gian mẫu và từng trường hợp xảy ra

-  Dùng công thức tính xác suất để tính.

Lời giải:

− Mỗi cách chọn ra đồng thời 3 viên bi trong hộp có 20 viên bi cho ta một tổ hợp chập 3 của 20 phần tử. Do đó, không gian mẫu Ω của phép thử trên gồm các tổ hợp chập 3 của 20 phần tử và 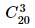$\left(\Omega \right)= =\; 1140.$

− Xét biến cố A: “3 viên bi lấy ra có đúng hai màu”.

Khi đó biến cố đối 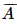 của A là: “3 viên bi lấy ra có 3 màu khác nhau hoặc có cùng màu”.

⦁ Trường hợp 1: Ba viên bi lấy ra có 3 màu khác nhau.

Có 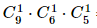= 270 cách chọn.

$⦁ Trường\; hợp\; 1: Ba\; viên\; bi\; lấy\; ra\; có\; cùng\; màu\; (cùng\; màu\; đỏ\; hoặc\; cùng\; màu\; xanh\; hoặc\; cùng\; màu\; vàng.$

$Có 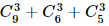=\; 114\; cách\; chọn.$

$Như\; vậy,\; số\; kết\; quả\; thuận\; lợi\; cho\; biến\; cố 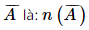=\; 270\; +\; 114\; =\; 384.$

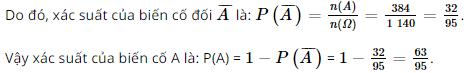
$Sachbaitap.com$