Giải SGK Toán 11 Cánh Diều tập 2 trang 54, 55

Bài 1 trang 54 SGK Toán 11 - Cánh Diều tập 2

Giải mỗi phương trình sau:

a)     \({\left( {0,3} \right)^{x - 3}} = 1\)

b)    \({5^{3x - 2}} = 25\)

c)     \({9^{x - 2}} = {243^{x + 1}}\)

d)    \({\log _{\frac{1}{2}}}(x + 1) =  - 3\)

e)     \({\log _5}(3x - 5) = {\log _5}(2x + 1)\)

f)      \({\log _{\frac{1}{7}}}(x + 9) = {\log _{\frac{1}{7}}}(2x - 1)\)

Phương pháp:

Dựa vào kiến thức đã học ở bài trên để làm bài

Lời giải:

a) (0,3)^x–3 = 1⇔ x – 3 = log_0,31 ⇔x – 3 = 0 ⇔x = 3.

Vậy phương trình đã cho có nghiệm là x=3.

b) 5^3x–2 = 25

⇔5^3x–2 = 5²

⇔ 3x – 2 = 2

⇔ 

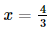
Vậy phương trình đã cho có nghiệm là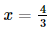 

c) 9^x–2 = 243^x+1⇔3^2x–4 = 3^5x+5

⇔ 2x – 4 = 5x + 5 ⇔ 3x = –9 ⇔ x = –3

Vậy phương trình đã cho có nghiệm là x = –3.

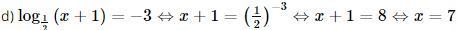
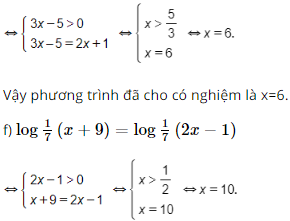
Vậy phương trình đã cho có nghiệm là x=10.

Bài 2 trang 55 SGK Toán 11 - Cánh Diều tập 2

Giải mỗi bất phương trình sau:

a)     \({3^x} > \frac{1}{{243}}\)

b)    \({\left( {\frac{2}{3}} \right)^{3x - 7}} \le \frac{3}{2}\)

c)     \({4^{x + 3}} \ge {32^x}\)

d)    \(\log (x - 1) < 0\)

e)     \({\log _{\frac{1}{5}}}(2x - 1) \ge {\log _{\frac{1}{5}}}(x + 3)\)

f)      \(\ln (x + 3) \ge \ln (2x - 8)\)

Phương pháp:

Dựa vào kiến thức đã học ở bài trên để làm bài

Lời giải:

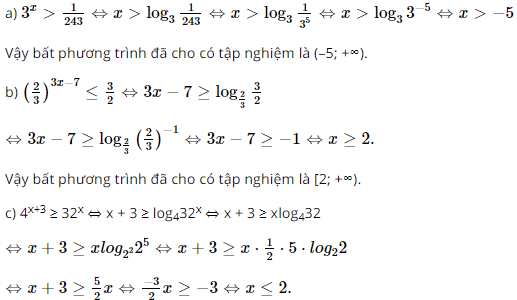
Vậy bất phương trình đã cho có tập nghiệm là (−∞; 2].

d) log(x – 1) < 0 ⇔0 < x – 1 < 10⁰

⇔0 < x – 1 < 1 ⇔1 < x < 2

Vậy bất phương trình đã cho có tập nghiệm là (1; 2).

Bài 3 trang 55 SGK Toán 11 - Cánh Diều tập 2

Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất x%/năm (x > 0). Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng. Tìm x, biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền về trong suốt quá trình gửi.

Phương pháp:

Áp dụng công thức tính lãi suất, thay số rồi tính

Lời giải:

Công thức tính số tiền rút được (cả gốc và lãi) sau n năm là: 100(1 + x%)ⁿ (triệu đồng).

Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng nên ta có:

100(1 + x%)³ = 119,1016

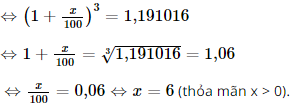
Vậy lãi xuất là 6% / năm.

Bài 4 trang 55 SGK Toán 11 - Cánh Diều tập 2

Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể chịu đựng được, biết rằng giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130 dB.

Phương pháp:

Dựa vào công thức tính mức cường độ âm để tính.

Lời giải:

Ta có công thức tính mức cường độ âm L (đơn vị dB) là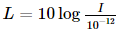 

Do giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB nên ta có L ≤ 130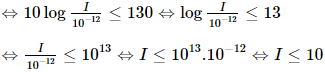

Vậy cường độ âmmà tai người có thể chịu đựng được là 10 W/m².

Sachbaitap.com