Giải SGK Toán 11 Cánh Diều tập 2 trang 63

Bài 1 trang 63 SGK Toán 11 - Cánh Diều tập 2

Tính đạo hàm của hàm số \(f(x) = 3{x^3} - 1\) tại điểm \({x_0} = 1\) bằng định nghĩa

Phương pháp:

Sử dụng định nghĩa đạo hàm để tính đạo hàm

Lời giải:

Xét ∆x là số gia của biến số tại điểm x₀ = 1.

Ta có ∆y = f(1 + ∆x) – f(1) = 3(1 + ∆x)³ – 1 – (3.1³ – 1)

              = 3 + 9∆x + 9.(∆x)² + 3(∆x)³ – 1 – 2

              = 9∆x + 9.(∆x)² + 3(∆x)³

              = ∆x[9 + 9∆x + 3(∆x)²].

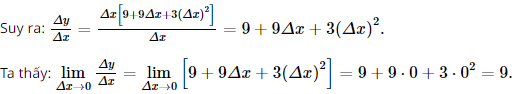
Bài 2 trang 63 SGK Toán 11 - Cánh Diều tập 2

Chứng minh rằng hàm số \(f(x) = \left| x \right|\) không có đạo hàm tại điểm \({x_0} = 0\), nhưng có đạo hàm tại mọi điểm \(x \ne 0\)

Phương pháp:

Tách \(f(x) = \left| x \right|\) thành 2 phần và tìm đạo hàm của từng phần.

Lời giải:

Xét ∆x là số gia của biến số tại điểm x0 = 0.

Ta có ∆y = f(0 + ∆x) – f(0) = |∆x| – |0| = |∆x|.

⦁ Với x > 0 ta có hàm số f(x) = x.

Xét ∆x là số gia của biến số tại điểm x > 0.

Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x) – x = ∆x.

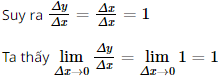
Do đó với x > 0 thì hàm số có đạo hàm f’(x) = 1.

⦁ Với x < 0 ta có hàm số f(x) = –x.

Xét ∆x là số gia của biến số tại điểm x < 0.

Ta có ∆y = f(x + ∆x) – f(x) = – (x + ∆x) + x = –∆x.

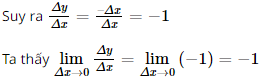
Do đó với x < 0 thì hàm số có đạo hàm f’(x) = –1.

Vậy hàm số f(x) = |x| không có đạo hàm tại x₀ = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0.

Bài 3 trang 63 SGK Toán 11 - Cánh Diều tập 2

Cho hàm số \(y =  - 2{x^2} + x\) có đồ thị (C).

a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)

Phương pháp:

 Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):

\(y = {k_0}(x - {x_0}) + {y_0}\)

Lời giải:

a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 có hệ số góc là:

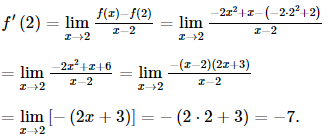
Vậy hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 là f’(x) = –7.

b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6) là: y = –7(x – 2) – 6 hay y = –7x + 8.

Bài 4 trang 63 SGK Toán 11 - Cánh Diều tập 2

Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là \(C(Q) = {Q^2} + 80Q + 3500\)

a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.

b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được

c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100.

Phương pháp:

Áp dụng quy tắc tính đạo hàm bằng định nghĩa để tính

Lời giải:

a) Xét ∆Q là số gia của biến số tại điểm Q.

Ta có ∆C = C(Q + ∆Q) – C(Q)

              = (Q + ∆Q)2 + 80(Q + ∆Q) + 3 500 – Q2 – 80Q – 3 500

              = (∆Q)2 + 2Q. ∆Q + 80∆Q.

              = ∆Q(∆Q + 2Q + 80).

Vậy hàm chi phí biên là: C’(Q) = 2Q + 80 (USD).

b) Ta có C’(90) = 2 . 90 + 80 = 260 (USD).

Ý nghĩa: Để sản xuất thêm 1 sản phẩm từ 90 lên 91 sản phẩm cần chi phí biên (chi phí gia tăng) là 260 (USD)

Sachbaitap.com