Giải SGK Toán 11 Kết nối tri thức tập 2 trang 14,15
Giải bài 6.9, 6.10, 6.11, 6.12, 6.13, 6.14 trang 14, 15 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Mức cường độ âm L đo bằng decibel (dB) của âm thanh có cường độ I (đo bằng oát trên mét vuông, kí hiệu W/m2) được định nghĩa như sau:
Bài 6.9 trang 14 SGK Toán 11 - Kết Nối Tri Thức tập 2
Tính:
a) \({\log _2}{2^{ - 13}};\)
b) \(\ln {e^{\sqrt 2 }};\)
c) \({\log _8}16 - {\log _8}2;\)
d) \({\log _2}6.{\log _6}8.\)
Phương pháp:
Sử dụng công thức \({\log _a}{a^\alpha } = \alpha ;{\log _a}\left( {\frac{M}{N}} \right) = {\log _a}M - {\log _a}N;{\log _a}M = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}.\)
Lời giải:
a) log22– 13 = – 13.
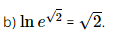
c) log816–log82=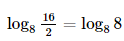 =1
=1
d) log26 . log68= log26 .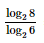 =
= 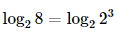 =3.
=3.
Bài 6.10 trang 14 SGK Toán 11 - Kết Nối Tri Thức tập 2
Viết mỗi biểu thức sau thành lôgarit của một biểu thức (giả thiết các biểu thức đều có nghĩa):
a) \(A = \ln \left( {\frac{x}{{x - 1}}} \right) + \ln \left( {\frac{{x + 1}}{x}} \right) - \ln \left( {{x^2} - 1} \right);\)
b) \(B = 21{\log _3}\sqrt[3]{x} + {\log _3}\left( {9{x^2}} \right) - {\log _3}9.\)
Phương pháp:
Sử dụng các công thức \({\log _a}{a^\alpha } = \alpha ;{\log _a}\left( {\frac{M}{N}} \right) = {\log _a}M - {\log _a}N;{\log _a}\left( {MN} \right) = {\log _a}M + {\log _a}N.\)
Lời giải:
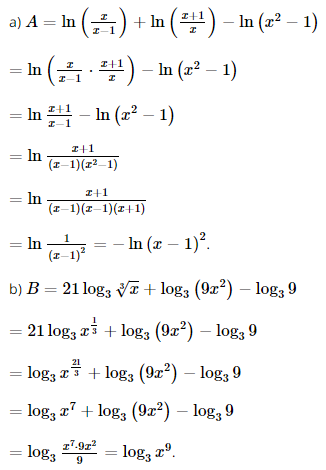
Bài 6.11 trang 15 SGK Toán 11 - Kết Nối Tri Thức tập 2
Rút gọn các biểu thức sau:
a) \(A = {\log _{\frac{1}{3}}}5 + 2{\log _9}25 - {\log _{\sqrt 3 }}\frac{1}{5};\)
b) \(B = {\log _a}{M^2} + {\log _{{a^2}}}{M^4}.\)
Phương pháp:
Sử dụng các công thức \({\log _{{a^\alpha }}}M = \frac{1}{\alpha }{\log _a}M;{\log _a}{M^\alpha } = \alpha {\log _a}M\)
Lời giải:
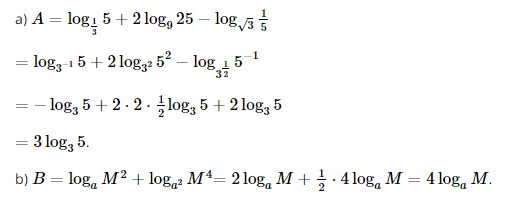
Bài 6.12 trang 15 SGK Toán 11 - Kết Nối Tri Thức tập 2
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
Phương pháp:
Sử dụng công thức \({\log _a}{M^\alpha } = \alpha {\log _a}M\) và từ công thức \({\log _a}M = \frac{{{{\log }_b}M}}{{{{\log }_b}a}} \Rightarrow {\log _b}M = {\log _b}a.{\log _a}M\)
Lời giải:
a) Áp dụng công thức đổi cơ số, ta có:
A = log23 ∙ log34 ∙ log45 ∙ log56 ∙ log67 ∙ log78
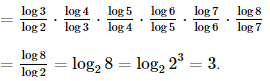
b) B = log22 ∙ log24 ∙∙∙ log22n
= log22 ∙ log222 ∙∙∙ log22n
= 1 ∙ 2 ∙ … ∙ n = n!.
Bài 6.13 trang 15 SGK Toán 11 - Kết Nối Tri Thức tập 2
Biết rằng độ cao tăng lên, áp suất không khí sẽ giảm và công thức tính áp suất dựa trên độ cao là
\(a = 15\,\,500\left( {5 - \log p} \right),\)
Trong đó a là độ cao so với mực nước biển (tính bằng mét) và p là áp suất không khí (tính bằng pascal).
Tính áp suất không khí ở đỉnh Everest có độ cao 8 850 m so với mực nước biển.
Phương pháp:
Áp dụng công thức \(a = 15\,\,500\left( {5 - \log p} \right)\)
Lời giải:
Ta có đỉnh Everest có độ cao 8 850 m so với mực nước biển nên a = 8 850.
Khi đó 15 500(5 – log p) = 8 850 ⇔ logp=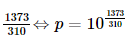 ≈26855,44.
≈26855,44.
Vậy áp suất không khí ở đỉnh Everest xấp xỉ 26 855,44 Pa.
Bài 6.14 trang 15 SGK Toán 11 - Kết Nối Tri Thức tập 2
Mức cường độ âm L đo bằng decibel (dB) của âm thanh có cường độ I (đo bằng oát trên mét vuông, kí hiệu W/m2) được định nghĩa như sau:
\(L\left( I \right) = 10\log \frac{I}{{{I_0}}},\)
trong đó \({I_0} = {10^{ - 12}}{\rm{W}}/{m^2}\) là cường độ âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe).
Xác định mức cường độ âm của mỗi âm sau:
a) Cuộc trò chuyện bình thường có cường độ \(I = {10^{ - 7}}{\rm{W}}/{m^2}.\)
b) Giao thông thành phố đông đúc có cường độ \(I = {10^{ - 3}}{\rm{W}}/{m^2}.\)
Phương pháp:
Sử dụng định nghĩa \(L\left( I \right) = 10\log \frac{I}{{{I_0}}}\)
Lời giải:
a) Mức cường độ âm của cuộc trò chuyện bình thường có cường độ I = 10– 7 W/m2 là
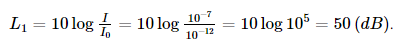
b) Mức cường độ âm của giao thông thành phố đông đúc có cường độ I = 10– 3 W/m2 là
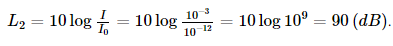
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 99, 100, 101 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 97 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96 (11/01)
- BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
- Hoạt động thực hành trải nghiệm Hình học
- HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
- Bài tập cuối chương 9
- Bài 33. Đạo hàm cấp hai
- Bài 32. Các quy tắc tính đạo hàm
- Bài 31. Định nghĩa và ý nghĩa của đạo hàm
- CHƯƠNG IX. ĐẠO HÀM
- Bài tập cuối chương 8
- Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
