Giải SGK Toán 11 Kết nối tri thức tập 2 trang 64, 65
Giải bài 7.33, 7.34, 7.35, 7.36, 7.37, 7.38, 7.39, 7.40, 7.41, 7.42, 7.43, 7.44, 7.45 trang 63 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và (OA = a,OB = asqrt 2 ) và (OC = 2a). Tính khoảng cách từ điểm (O) đến mặt phẳng ((ABC)).
Xem thêm: Bài tập cuối chương 7
Bài 7.33 trang 64 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho các phát biểu sau:
(1) Hai mặt phẳng \((P)\) và \((Q)\) có giao tuyến là đường thẳng a và cùng vuông góc với mặt phẳng \((R)\) thì \(a \bot (R)\).
(2) Hai mặt phẳng \((P)\) và \((Q)\) vuông góc với nhau và có giao tuyến là đường thẳng a, một đường thẳng \(b\) nằm trong mặt phẳng \((P)\) và vuông góc với đường thẳng \(a\) thì \(b \bot (Q)\).
(3) Mặt phẳng \(({\rm{P}})\) chứa đường thẳng a và a vuông góc với \((Q)\) thì \((P) \bot (Q)\).
(4) Đường thẳng a nằm trong mặt phẳng \((P)\) và mặt phẳng \((P)\) vuông góc với mặt phẳng (Q) thì \(a \bot (Q)\).
Số phát biểu đúng trong các phát biểu trên là:
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp:
Dựa vào lý thuyết đã học của chương
Lời giải:
Đáp án đúng là: C
+)
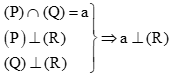 nên (1) đúng.
nên (1) đúng.
+)
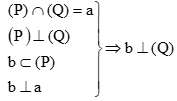 nên (2) đúng.
nên (2) đúng.
+)
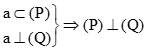 nên (3) đúng.
nên (3) đúng.
+)
 ta chưa kết luận được a ⊥">⊥⊥ (Q) vì có thể xảy ra trường hợp song song nên (4) sai.
ta chưa kết luận được a ⊥">⊥⊥ (Q) vì có thể xảy ra trường hợp song song nên (4) sai.
Bài 7.34 trang 64 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho mặt phẳng \((P)\) vuông góc với mặt phẳng \((Q)\) và a là giao tuyến của \((P)\) và \((Q)\). Trong các phát biểu dưới đây, phát biểu nào đúng?
\(A\). Đường thẳng \(d\) nằm trên \((Q)\) thì \(d\) vuông góc với \((P)\).
\(B\). Đường thẳng \(d\) nằm trên \((Q)\) và \(d\) vuông góc với a thì d vuông góc với \((P)\).
C. Đường thẳng \(d\) vuông góc với a thì \(d\) vuông góc với \((P)\).
D. Đường thẳng \(d\) vuông góc với \((Q)\) thì \(d\) vuông góc với \((P)\).
Phương pháp:
Dựa vào lý thuyết đã học của chương
Lời giải:
Đáp án đúng là: B
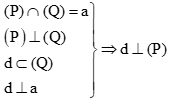
Bài 7.35 trang 64 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng?
\(A\). Số đo của góc nhị diện [S, AB, C] bằng \(\widehat {SBC}\).
B. Số đo của góc nhị diện [D, SA, B] bằng \({90^0}\).
C. Số đo của góc nhị diện [S, AC, B] bằng \({90^0}\).
D. Số đo của góc nhị diện [D, SA, B] bằng \(\widehat {BSD}\).
Phương pháp:
Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải:
Đáp án đúng là: C

Gọi O là giao điểm của AC và BD. Kẻ OE ⊥ AB tại E.
Do ABCD là hình vuông nên O là trung điểm của AC và BD.
Xét tam giác ABD có OE // AD (do cùng vuông góc với AB) mà O là trung điểm của BD nên E là trung điểm của AB.
Xét tam giác SAB có SA = SB (do S.ABCD là hình chóp tứ giác đều) nên SAB là tam giác cân tại S mà SE là trung tuyến nên SE đồng thời là đường cao hay SE ⊥ AB.
Do đó [S, AB, C] = 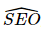 , suy ra A sai.
, suy ra A sai.
Vì ABCD là hình vuông nên BO ⊥ AC, S.ABCD là hình chóp đều nên SO ⊥ (ABCD) suy ra SO ⊥ AC, SO ⊥ BD .
Vì BO ⊥ AC, SO ⊥ AC nên [S, AC, B] = 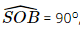 , suy ra C đúng.
, suy ra C đúng.
Kẻ DF ⊥ SA tại F.
Vì SO ⊥ BD và AC ⊥ SA nên [D, SA, B] = 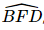 , suy ra B, D sai.
, suy ra B, D sai.
Bài 7.36 trang 64 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot (ABCD)\).
Phát biểu nào sau đây là sai?
\(A\). Đường thẳng BC vuông góc với mặt phẳng \((SAB)\).
B. Đường thẳng BD vuông góc với mặt phẳng \((SAC)\).
C. Đường thẳng AC vuông góc với mặt phẳng \((SBD)\).
D. Đường thẳng AD vuông góc với mặt phẳng \((SAB)\).
Phương pháp:
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải:
Đáp án đúng là: C

Vì ABCD là hình vuông nên AB ⊥ BC mà SA ⊥ (ABCD) nên SA ⊥ BC.
Có AB ⊥ BC và SA ⊥ BC nên BC ⊥ (SAB). Vậy A đúng.
Vì ABCD là hình vuông nên AC⊥ BD mà SA ⊥ (ABCD) nên SA ⊥ BD.
Có AC ⊥ BD và SA ⊥ BD nên BD ⊥ (SAC). Vậy B đúng.
Vì ABCD là hình vuông nên AD⊥AB mà SA ⊥ (ABCD) nên SA ⊥ AD.
Có AD ⊥ AB và SA ⊥ AD nên AD ⊥ (SAB). Vậy D đúng.
Bài 7.37 trang 64 SGK Toán 11 - Kết Nối Tri Thức tập 2
Thể tích của khối chóp có diện tích đáy bằng \({\bf{S}}\), chiều cao bằng \(h\) là:
A. \(V = {\bf{S}}.h\).
B. \(V = \frac{1}{2}{\bf{S}}.h\).
C. \(V = \frac{1}{3}{\bf{S}}.h\).
D. \(V = \frac{2}{3}{\bf{S}}.h\).
Phương pháp:
Công thức tính thể tích khối chóp
Lời giải:
Đáp án đúng là: C
Ta có thể tích khối chóp là V =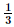 .S.h.
.S.h.
Bài 7.38 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và \(OA = a,OB = a\sqrt 2 \) và \(OC = 2a\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \((ABC)\).
Phương pháp:
Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P).
Lời giải:
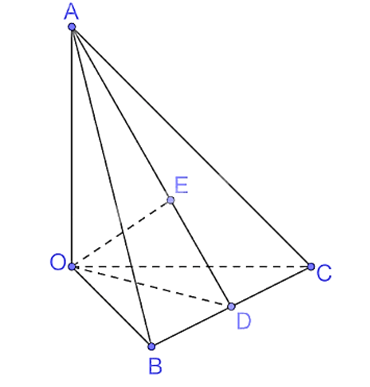
Kẻ OD ⊥ BC tại D.
Có OA ⊥ OB, OA ⊥ OC nên OA ⊥ (OBC), suy ra OA ⊥ BC mà OD ⊥ BC nên
BC ⊥ (OAD).
Kẻ OE ⊥ AD tại E.
Vì BC ⊥ (OAD) nên BC ⊥ OE mà OE ⊥ AD nên OE ⊥ (ABC).
Do đó d(O, (ABC)) = OE.
Xét tam giác OBC vuông tại O, OD là đường cao có:
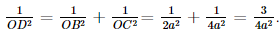
Vì OA ⊥ (OBC) nên OA ⊥ OD.
Xét tam giác AOD vuông tại O, OE là đường cao nên
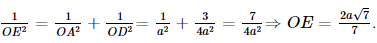
Vậy d(O, (ABC))= 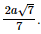
Bài 7.39 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.
Phương pháp:
- Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
- Hai mặt phẳng vuông góc nếu trong mặt phẳng này có một đường thẳng vuông góc vào giao tuyến thì đường thẳng đó vuông góc với mặt phẳng còn lại.
- Đường thẳng \(\Delta \) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Lời giải:
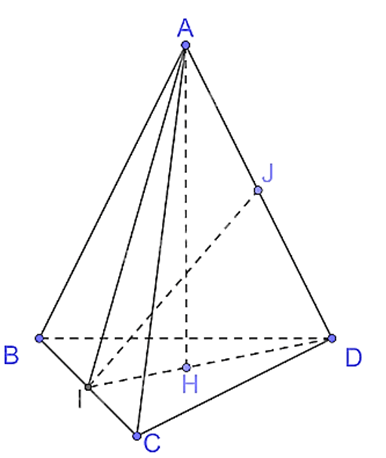
a) Vì tam giác ABC cân tại A, AI là trung tuyến nên AI đồng thời là đường cao hay AI ⊥ BC.
Vì tam giác BCD cân tại D, DI là trung tuyến nên DI đồng thời là đường cao hay DI ⊥ BC.
Có AI ⊥ BC và DI ⊥ BC nên BC ⊥ (AID).
b) Do AH là đường cao của tam giác AID nên AH ⊥ DI.
Vì BC ⊥ (AID) nên BC ⊥ AH mà AH ⊥ DI nên AH ⊥ (BCD).
c) Vì BC ⊥ (AID) nên BC ⊥ IJ, mà IJ là đường cao của tam giác AID nên IJ ⊥ AD. Do đó IJ là đường vuông góc chung của AD và BC.
Bài 7.40 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,BC = \) a và \(\widehat {CAB} = {30^0}\). Biết \(SA \bot (ABC)\) và \(SA = a\sqrt 2 \).
a) Chứng minh rằng \((SBC) \bot (SAB)\).
b) Tính theo a khoảng cách từ điểm \(A\) đến đường thẳng SC và khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
Phương pháp:
- Hai mặt phẳng được gọi là vuông góc nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.
- Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P).
Lời giải:

a) Do tam giác ABC vuông tại B nên AB ⊥ BC.
Vì SA ⊥ (ABC) nên SA ⊥ BC mà AB ⊥ BC nên BC ⊥ (SAB), suy ra (SBC) ⊥ (SAB).
b) Kẻ AD ⊥ SC tại D. Khi đó d(A, SC) = AD.
Vì SA ⊥ (ABC) nên SA ⊥ AC nên tam giác SAC vuông tại A.
Xét tam giác ABC vuông tại B, sin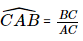
⇒AC = 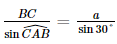 = 2a.
= 2a.
Xét tam giác SAC vuông tại A, AD là đường cao, có:
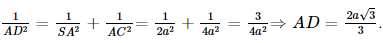
Vậy d(A, SC) =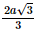 .
.
Kẻ AE ⊥ SB tại E.
Vì BC ⊥ (SAB) nên BC ⊥ AE mà AE ⊥ SB nên AE ⊥ (SBC).
Khi đó d(A, (SBC)) = AE.
Xét tam giác ABC vuông tại B, có AB = 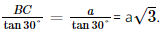
Vì SA ⊥ (ABC) nên SA ⊥ AB, suy ra tam giác SAB vuông tại A.
Xét tam giác SAB vuông tại A, AE là đường cao, có: 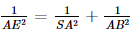 .
.
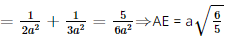
Vậy d(A, (SBC)) = 
Bài 7.41 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại \(S\) và \((SAD) \bot (ABCD)\).
a) Tính theo a thể tích của khối chóp S.ABCD.
b) Tính theo a khoảng cách giữa hai đường thẳng AD và SC.
Phương pháp:
- Thể tích khối chóp \(V = \frac{1}{3}h.S\)
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
Lời giải:
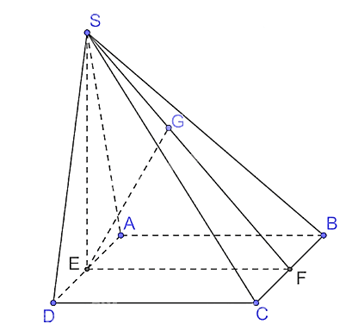
a) Kẻ SE ⊥ AD tại E. Vì tam giác SAD vuông cân tại S nên E là trung điểm của AD.
Có (SAD) ⊥ (ABCD), (SAD) ∩ (ABCD) = AD, SE ⊥ AD nên SE ⊥ (ABCD).
Vì tam giác SAD vuông cân tại S, SE là trung tuyến nên SE = 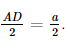
Khi đó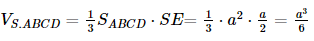 .
.
b) Do ABCD là hình vuông nên AD // BC mà BC ⊂ (SBC) nên AD // (SBC).
Khi đó d(AD, SC) = d(AD, (SBC)) = d(E, (SBC)).
Kẻ EF // AB (F thuộc BC). Khi đó EF ⊥ BC (vì AB ⊥ BC).
Mà SE ⊥⊥ (ABCD) nên SE ⊥ BC mà EF ⊥ BC nên BC ⊥ (SEF).
Lại có BC ⊂ (SBC) nên (SBC) ⊥ (SEF) và (SBC) ∩ (SEF) = SF.
Kẻ EG ⊥ SF tại G nên EG ⊥ (SBC). Khi đó d(E, (SBC)) = EG.
Do ABCD là hình vuông nên EF = AB = a.
Xét tam giác SEF vuông tại E, EG là đường cao, có
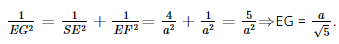
Vậy d(AD, SC) = 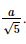
Bài 7.42 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình hộp \(ABCD.A'B'C'D'\) có độ dài tất cả các cạnh bằng \(a,AA' \bot (ABCD)\) và \(\widehat {BAD} = {60^0}\).
a) Tính thể tích của khối hộp \(ABCD.A'B'C'D'\).
b) Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {A'BD} \right)\).
Phương pháp:
- Thể tích của khối hộp bằng tích của diện tích một mặt và chiều cao của khối hộp ứng với mặt đó.
- Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P).
Lời giải:
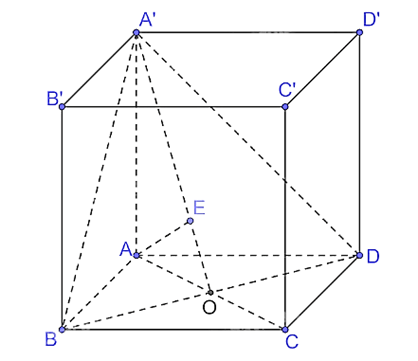
a) Gọi O là giao điểm của AC và BD.
Vì hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a nên ABCD là hình thoi, suy ra AO = OC và AC ⊥ BD.
Có 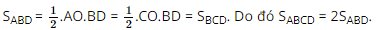
Mà 
Vậy 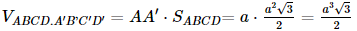
b) Vì AO ⊥ BD mà AA' ⊥ (ABCD) nên AA' ⊥ BD. Do đó BD ⊥ (AOA').
Suy ra (A'BD) ⊥ (AOA').
Kẻ AE ⊥ A'O tại E. Vì (A'BD) ⊥ (AOA'), (A'BD) ∩ (AOA') = A'O và AE ⊥ A'O nên AE ⊥ (A'BD). Do đó d(A, (A'BD)) = AE.
Xét tam giác ABD có AB = AD = a nên tam giác ABD là tam giác cân tại A mà 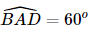 nên tam giác ABD đều, suy ra BD = a mà BO =
nên tam giác ABD đều, suy ra BD = a mà BO =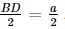 .
.
Xét tam giác AOB vuông tại O, có AO =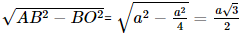
Vì AA' ⊥ (ABCD) nên AA' ⊥ AO hay tam giác A'AO vuông tại A.
Xét tam giác A'AO vuông tại A có 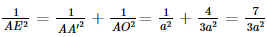
⇒AE= 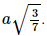
Vậy d(A, (A'BD)) = 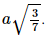
Bài 7.43 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
Phương pháp:
Thể tích khối lăng trụ \(V = h.S\)
Lời giải:
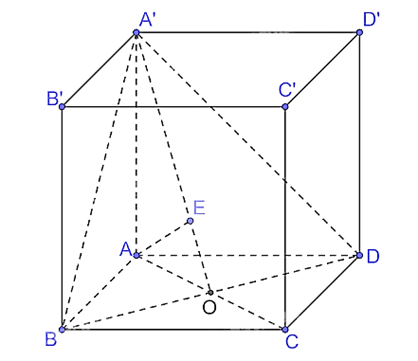
a) Gọi O là giao điểm của AC và BD.
Do A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a nên A'O ⊥ (ABCD). Vì ABCD là hình vuông cạnh a nên SABCD = a2.
Xét tam giác ABC vuông tại B, có AC =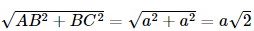 mà O là trung điểm của AC nên AO =
mà O là trung điểm của AC nên AO =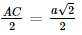 .
.
Xét tam giác A'AO vuông tại O, có A'O = 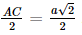
Khi đó 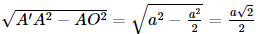
Ta có 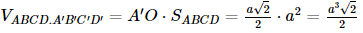
Khi đó ta thấy khối chóp A'.BB'C'C và khối lăng trụ AA'D'D.BB'C'C có chung đường cao và đáy nên 
Bài 7.44 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
Phương pháp:
Thể tích khối lăng trụ \(V = h.S\)
Lời giải:

Gọi O là giao điểm của AC và BD.
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) nên SO ⊥ (ABCD).
Kẻ AH ⊥ DC tại H, BK ⊥ DC tại K.
Khi đó ABKH là hình chữ nhật nên AB = HK = a.
Xét ∆AHD và ∆BKC có: AD = BC = a,  (do ABCD là hình thang cân).
(do ABCD là hình thang cân).
Do đó ∆AHD = ∆BKC, suy ra DH = CK =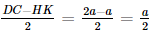
CH = HK + CK = a+ 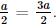
Xét tam giác AHD vuông tại H, có AH = 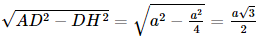
Xét tam giác AHC vuông tại H, có AC = 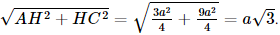
Vì AB // CD nên 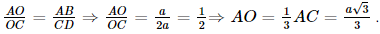
Xét tam giác SOA vuông tại O, có SO =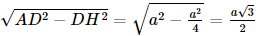
Khi đó d(S, (ABCD)) = 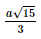
Ta có 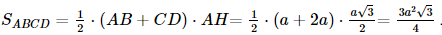
=a153">Vậy 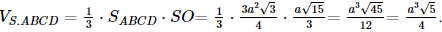
Bài 7.45 trang 65 SGK Toán 11 - Kết Nối Tri Thức tập 2
Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng \(10\;{\rm{m}}\) và tạo với mặt đất góc \({80^0}\). Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài \(12\;{\rm{m}}\) vào tạo với cây cột một góc bằng \({120^0}\) (tức là \(\widehat {ABC} = {120^0}\)). Tính góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên.
Phương pháp:
Định lý cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Lời giải:
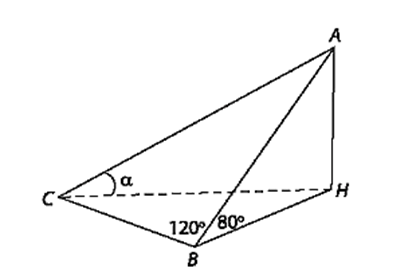
Gọi H là hình chiếu vuông góc của A lên mặt đất. Khi đó AH ⊥ (BCH).
Ta có góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời là 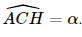
Xét tam giác AHB vuông tại H, có AH = AB . sin80° = 10 . sin80° (m).
Áp dụng định lí Côsin trong tam giác ABC, có:
AC2 = AB2 + BC2 – 2.AB.BC.cos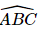
= 102 + 122 – 2.10.12.cos120° = 364
⇒ AC = 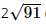
Xét tam giác AHC vuông tại H, có 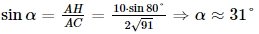
Vậy góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên khoảng 31°.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 99, 100, 101 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 97 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96 (11/01)
- BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
- Hoạt động thực hành trải nghiệm Hình học
- HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
- Bài tập cuối chương 9
- Bài 33. Đạo hàm cấp hai
- Bài 32. Các quy tắc tính đạo hàm
- Bài 31. Định nghĩa và ý nghĩa của đạo hàm
- CHƯƠNG IX. ĐẠO HÀM
- Bài tập cuối chương 8
- Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!