Giải SGK Toán 11 trang 109 Cánh Diều tập 1
Giải bài 1, 2, 3, 4 trang 109 SGK Toán lớp 11 Cánh Diều tập 1. Bài 1. Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
Bài 1 trang 109 SGK Toán 11 tập 1 - Cánh Diều
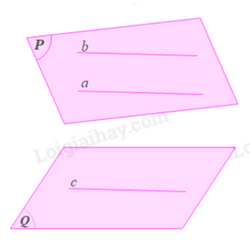
Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
Phương pháp:
Theo dấu hiệu nhận biết hai mặt phẳng song song:
Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải:
Trường hợp a cắt b theo dấu hiệu nhận biết hai mặt phẳng song song thì ý kiến đúng
Trường hợp a không cắt b thì a // b
Ta có: a thuộc (P), a // (Q)
B thuộc (P), b // (Q)
Do đó: (P) // (Q)
Vậy ý kiến đúng
Bài 2 trang 109 SGK Toán 11 tập 1 - Cánh Diều
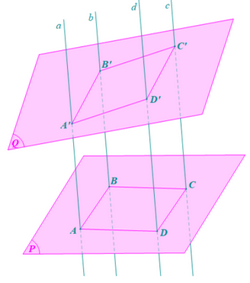
• Ta có: AB // CD (do ABCD là hình bình hành).
Mà CD ⊂ mp(CDD’C’) nên AB // (CDD’C’).
Mà D’D ⊂ mp(CDD’C’) nên A’A // (CDD’C’).
Ta có: AB // (CDD’C’);
A’A // (CDD’C’);
AB, A’A cắt nhau tại A và cùng nằm trong (ABB’A’)
Do đó (ABB’A’) // (CDD’C’).
Ta có: (ABB’A’) // (CDD’C’);
(ABB’A’) ∩ (Q) = A’B’;
(CDD’C’) ∩ (Q) = C’D’.
Do đó A’B’ // C’D’.
• Tương tự, (ADD’A’) // (BCC’B);
(ADD’A’) ∩ (Q) = A’D’;
(BCC’B) ∩ (Q) = B’C’.
Do đó A’D’ // B’C’.
Tứ giác A’B’C’D’ có A’B’ // C’D’ và A’D’ // B’C’ nên A’B’C’D là hình bình hành.
Bài 3 trang 109 SGK Toán 11 tập 1 - Cánh Diều
Cho tứ diện ABCD. Lấy \({G_1},{G_2},{G_3}\)lần lượt là trọng tâm của các tam giác ABC, ACD, ADB.
a) Chứng minh rằng \(({G_1}{G_2}{G_3})//(BCD)\)
b) Xác định giao tuyến của mặt phẳng \(({G_1}{G_2}{G_3})\) với mặt phẳng \((ABD)\)
Phương pháp:
Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải:
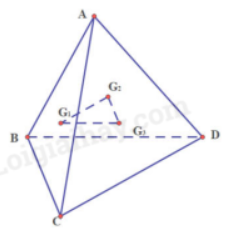
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\)
mà \({G_3}\) là điểm chung của hai mặt phẳng
Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\)
Vậy \({G_3}x\) là giao tuyến cấn tìm
Bài 4 trang 109 SGK Toán 11 tập 1 - Cánh Diều
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng (AFD) // (BEC)
b) Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Lấy N là giao điểm của (P) và AC. Tính \(\frac{{AN}}{{NC}}\)
Phương pháp:
Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải:
a)
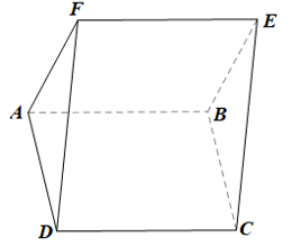
Ta có: BE // AF (do ABEF là hình bình hành);
AF ⊂ (AFD)
Do đó BE // (AFD).
Ta cũng có: BC // AD (do ABCD là hình bình hành)
AD ⊂ (AFD)
Do đó BC // (AFD).
Do BE // (AFD);
BC // (AFD);
BE, BC cắt nhau tại điểm B và cùng nằm trong mp(BEC)
Suy ra (AFD) // (BEC).
b)
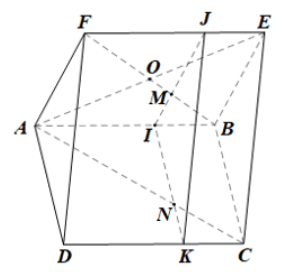
+) Do (AFD) song song với (P) nên tồn tại hai đường thẳng trong (AFD) song song với (P).
• Trong mp(ABEF), qua điểm M vẽ đường thẳng song song với AF, đường thẳng này cắt AB, EF lần lượt tại I, J.
Khi đó IJ // AF, mà AF ⊂ (AFD) nên IJ // (AFD).
• Trong mp(ABCD), qua điểm I vẽ đường thẳng song song với AD, cắt CD tại K.
Khi đó IK // AD, mà AD ⊂ (AFD) nên IK // (AFD).
• Ta có: IJ // (AFD);
IK // (AFD);
IJ, IK cắt nhau tại điểm I và cùng nằm trong mp(IJK).
Do đó (IJK) // (AFD).
Mà M ∈ IJ, IJ ⊂ (IJK) nên mp (P) đi qua M và song song với (AFD) chính là mp(IJK).
+) Trong mp(ABCD), AC cắt IK tại N, khi đó N là giao điểm của AC và (P).

Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 8
- Bài 6. Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
- Bài 5. Khoảng cách
- Bài 4. Hai mặt phẳng vuông góc
- Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- CHƯƠNG VIII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN, PHÉP CHIẾU VUÔNG GÓC
- Bài tập cuối chương 7
- Bài 3. Đạo hàm cấp hai
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
