Giải SGK Toán 11 trang 118 Kết Nối Tri Thức tập 1
Giải bài 5.7, 5.8, 5.9, 5.10, 5.11, 5.12, 5.13 trang 118 SGK Toán lớp 11 Kết Nối Tri Thức tập 1. Tính các giới hạn một bên:
Bài 5.8 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Tính các giới hạn sau:
a) \(\mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{{{\left( {x + 2} \right)}^2} - 4}}{x}\);
b) \(\mathop {{\rm{lim}}}\limits_{x \to 0} \) \(\frac{{\sqrt {{x^2} + 9} - 3}}{{{x^2}}}\)
Phương pháp:
a, Phân tích đa thức thành nhân tử.
b, Nhân cả tử và mẫu với biểu thức liên hợp của tử \((\sqrt A + B).(\sqrt A - B) = A - {B^2}\).
Lời giải:
Do mẫu thức có giới hạn là 0 khi x ⟶ 0 nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số đối với cả hai câu a và b.
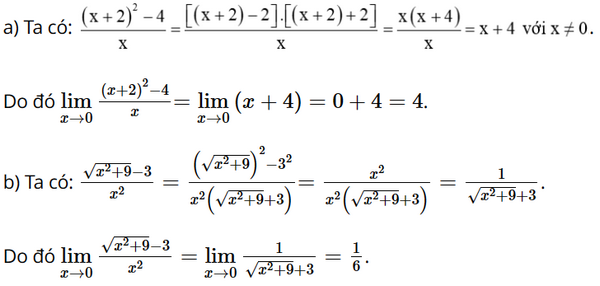
Bài 5.9 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Cho hàm số \(H(t) = \left\{ \begin{array}{l}0,t < 0\\1,t \ge 0\end{array} \right.\) (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thười điểm t = 0).
Tính \(\mathop {{\rm{lim}}}\limits_{t \to {0^ + }} H\left( t \right)\) và \(\mathop {{\rm{lim}}}\limits_{t \to 0} \;H\left( t \right).\)
Phương pháp:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta có hàm số \(f\left( x \right)\) có giới hạn là số L khi \(x \to + \infty \) nếu dãy số \(\left( {{x_n}} \right)\) bất kỳ, \({x_n} > a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L,\) kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\;\)hay \(f\left( x \right) \to L\) khi \(x \to + \infty \).
Lời giải:
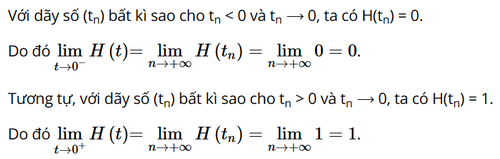
Bài 5.10 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Tính các giới hạn một bên:
a) \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \frac{{x - 2}}{{x - 1}}\);
b) \(\mathop {{\rm{lim}}}\limits_{x \to {4^ - }} \frac{{{x^2} - x + 1}}{{4 - x}}\)
Phương pháp:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a;\;{x_0}} \right)\). Ta nói hàm số \(f\left( x \right)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \(a < {x_n} < {x_0},\;{x_n} \to {x_0}\), ta có \(f\left( {{x_n}} \right) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải:
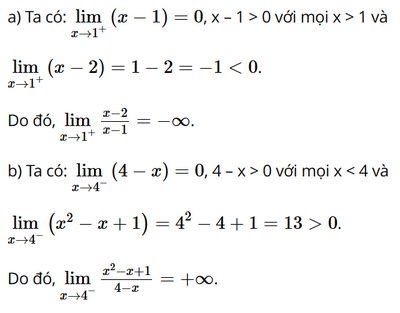
Bài 5.11 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Cho hàm số \(g\left( x \right) = \frac{{{x^2} - 5x + 6}}{{\left| {x - 2} \right|}}\)
Tìm \(\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} g\left( x \right)\) và \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} g\left( x \right)\).
Phương pháp:
Áp dụng giới hạn trái, phải để tính.
\(\left| a \right| = \left\{ \begin{array}{l} - a,a < 0\\a,a \ge 0\end{array} \right.\)
Lời giải:

Bài 5.12 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Tính các giới hạn sau:
a) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{1 - 2x}}{{\sqrt {{x^2} + 1} }}\)
b) \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right)\)
Phương pháp:
a, Chia cả tử và mẫu cho \({x^n}\) n là số mũ lớn nhất.
b, Nhân với biểu thức liên hợp \((\sqrt A + B).(\sqrt A - B) = A - {B^2}\).
Lời giải:
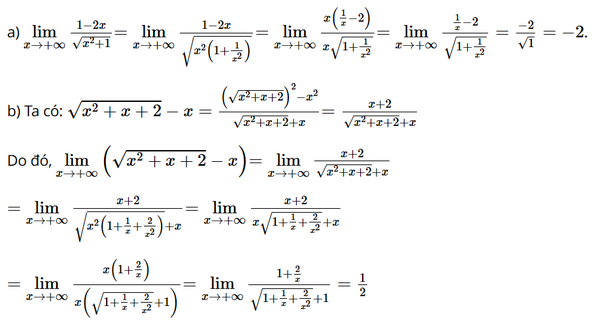
Bài 5.13 trang 118 SGK Toán 11 tập 1 - Kết Nối Tri Thức
Cho hàm số \(f\left( x \right) = \frac{2}{{\left( {x - 1} \right)\left( {x - 2} \right)}}\)
Tìm \(\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} f\left( x \right)\) và \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} f\left( x \right)\)
Phương pháp:
Áp dụng giới hạn trai, giới hạn phải để tính.
Phương pháp:
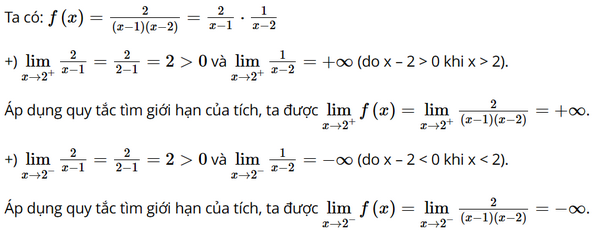
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 105, 106 (14/03)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 99, 100, 101 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 97 (11/01)
- Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96 (11/01)
- BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
- Hoạt động thực hành trải nghiệm Hình học
- HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
- Bài tập cuối chương 9
- Bài 33. Đạo hàm cấp hai
- Bài 32. Các quy tắc tính đạo hàm
- Bài 31. Định nghĩa và ý nghĩa của đạo hàm
- CHƯƠNG IX. ĐẠO HÀM
- Bài tập cuối chương 8
- Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
