Giải SGK Toán 5 Cánh Diều trang 12, 13, 14 tập 1

Bài 1 (Trang 12, SGK Toán 5 - Cánh Diều tập 1)

Trò chơi “Ghép thẻ”

a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:

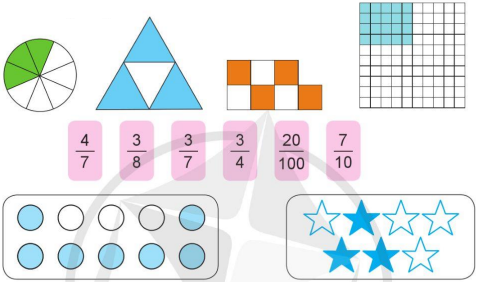
b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.

Phương pháp:

a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau.

b)

- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.

- Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

Lời giải:

a)

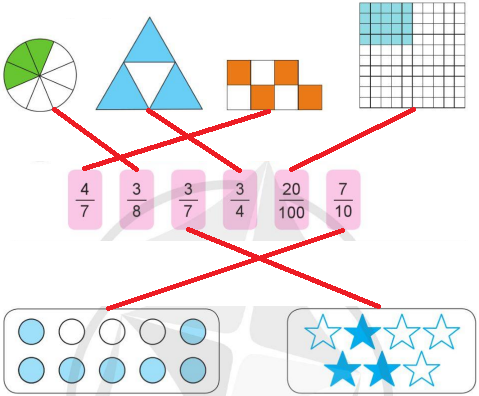
b)

\(\frac{4}{{7}}\) đọc là: bốn phần bảy; tử số là 4, mẫu số là 7

\(\frac{3}{{8}}\) đọc là: ba phần tám; tử số là 3, mẫu số là 8

\(\frac{3}{{7}}\) đọc là: ba phần bảy; có tử số là 3, mẫu số là 7

\(\frac{3}{{4}}\) đọc là: ba phần tư; tử số là 3, mẫu số là 4

\(\frac{20}{{100}}\) đọc là: hai mươi phần một trăm; tử số là 20, mẫu số là 100

\(\frac{7}{{10}}\) đọc là: bảy phần mười; tử số là 7, mẫu số là 10

Bài 2 (Trang 12, 13 SGK Toán 5 - Cánh Diều tập 1)

a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu):

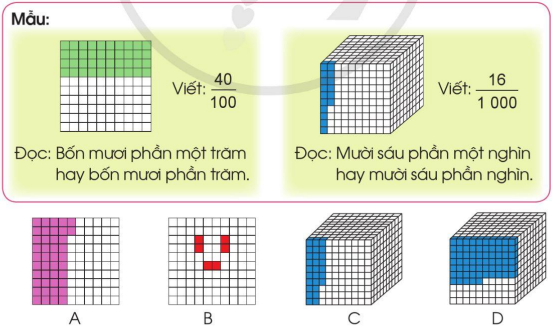
b) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

c) Viết các số tự nhiên sau thành phân số (theo mẫu):

Phương pháp:

a) Phân số chỉ phần đã tô màu có tử số chỉ số phần đã tô màu và mẫu số chỉ số phần bằng nhau.

Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.

b) Thương của phép chia một số tự nhiên cho một số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

c) Mọi số tự nhiên đều có thể viết thành phân số có mẫu số là 1.

Lời giải:

a) Hình A

Viết \(\frac{42}{{100}}\)

Đọc: Bốn mươi hai phần một trăm hay bốn mươi hai phần trăm

b) Hình B

Viết \(\frac{6}{{100}}\)

Đọc: Sáu phần một trăm hay sáu phần trăm

c) Hình C

Viết \(\frac{27}{{1000}}\)

Đọc: Hai mươi bảy phần một nghìn hay hai bảy phần nghìn

d) Hình D

Viết \(\frac{65}{{1000}}\)

Đọc: Sáu mươi lăm phần một nghìn hay sáu mươi lăm phần nghìn

b)

11 : 5 = \(\frac{11}{{5}}\)

9 : 100 = \(\frac{9}{{100}}\)

33 : 30 = \(\frac{33}{{30}}\)

c)

Viết các số tự nhiên sau thành phân số (theo mẫu):

Mẫu: 4 = \(\frac{4}{{1}}\)

301 = \(\frac{301}{{1}}\)

12 = \(\frac{12}{{1}}\)

2 025  = \(\frac{2025}{{1}}\)

Bài 3 (Trang 13, SGK Toán 5 - Cánh Diều tập 1)

a) Nêu hai phân số bằng mỗi phân số sau: \(\frac{5}{{4}}\) ; \(\frac{9}{{12}}\)

b) Rút gọn các phân số sau: \(\frac{24}{{32}}\) ; \(\frac{14}{{35}}\) ; \(\frac{30}{{25}}\) ; \(\frac{63}{{36}}\)

Phương pháp:

a) Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

 Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

b) Rút gọn phân số:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

- Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải:

Bài 4 (Trang 13, SGK Toán 5 - Cánh Diều tập 1)

Quy đồng mẫu số hai phân số:

Phương pháp:

- Tìm mẫu số chung

- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng

- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được

Lời giải:

Bài 5 (Trang 13, SGK Toán 5 - Cánh Diều tập 1)

a) Đọc ví dụ sau rồi nói cho bạn nghe cách thực hiện:

Ví dụ: Quy đồng mẫu số hai phân số \(\frac{2}{{3}}\) và \(\frac{5}{{4}}\)

Vì 3 × 4 = 12 nên ta chọn 12 làm mẫu số chung.

Ta có:

Vậy quy đồng mẫu số hai phân số \(\frac{2}{{3}}\) và \(\frac{5}{{4}}\) và ta được \(\frac{8}{{12}}\) và \(\frac{15}{{12}}\)

b) Quy đồng mẫu số hai phân số:

Phương pháp:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Lời giải:

Bài 6 (Trang 14, SGK Toán 5 - Cánh Diều tập 1)

Quy đồng mẫu số hai phân số:

Lưu ý: Khi quy đồng mẫu số hai phân số khác mẫu số, ta nên chọn số bé nhất (lớn hơn 0) chia hết cho cả hai mẫu số làm mẫu số chung.

Ví dụ: Quy đồng mẫu số hai phân số \(\frac{2}{{9}}\) và \(\frac{5}{{6}}\)

Vì 18 là số bé nhất lớn hơn 0 chia hết cho 9 và 6 nên ta hcojn 18 làm mẫu số chung.

Ta có:

\(\frac{2}{{9}}\) = \(\frac{2x2}{{9x2}}\) = \(\frac{4}{{18}}\) và \(\frac{5}{{6}}\) = \(\frac{5x3}{{6x3}}\) = \(\frac{15}{{18}}\)

Vậy quy đồng mẫu số hai phân số \(\frac{2}{{9}}\) và \(\frac{5}{{6}}\) ta được \(\frac{4}{{18}}\) và \(\frac{15}{{18}}\)

Phương pháp:

- Tìm mẫu số chung

- Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng

- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được

Lời giải:

Bài 7 (Trang 14, SGK Toán 5 - Cánh Diều tập 1)

a) >, <,= ?

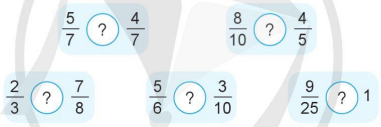
b) Sắp xếp các phân số \(\frac{2}{{3}}\) ; \(\frac{6}{{7}}\) ; \(\frac{3}{{4}}\)theo thứ tự từ bé đến lớn.

Phương pháp:

- Trong hai phân số có cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.

 - Muốn so sánh hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng

Lời giải:

a)

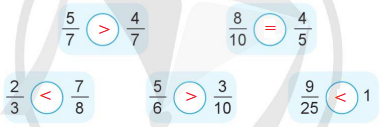
b)

Chọn mẫu số chung là 84.

Ta có:

Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là \(\frac{2}{{3}}\) ; \(\frac{3}{{4}}\) ; \(\frac{6}{{7}}\)

Bài 8 (Trang 14, SGK Toán 5 - Cánh Diều tập 1)

Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được \(\frac{5}{{8}}\) sợi dây. Đức leo được \(\frac{4}{{10}}\) sợi dây.

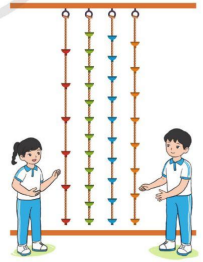
Theo em:

a) Dung đã leo sợi dây màu nào? Đức đã leo sợi dây màu nào?

b) Ai đã leo được đoạn dây dài hơn?

Phương pháp:

a) Quan sát hình vẽ và đếm số phần trên mỗi sợi dây.

Sợi dây mỗi bạn leo có mẫu số bằng số phần vừa đếm được.

b) So sánh số phần dây Dung leo được với số phần dây Phúc leo được rồi kết luận

Lời giải:

a) Dung đã leo được sợi dây màu cam vì sợi dây màu cam được chia thành 8 phần bằng nhau, Đức đã leo được sợi dây màu xanh dương vì sợi dây màu xanh dương được chia thành 10 phần bằng nhau.

b) Chọn 40 là mẫu số chung. Ta có:

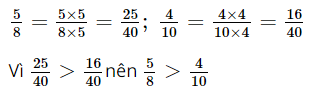
Vậy Dung leo được đoạn dây dài hơn Đức.

Sachbaitap.com