Giải SGK Toán 8 Cánh Diều tập 2 trang 60, 61

Bài 1 trang 60 SGK Toán 8 - Cánh Diều tập 2

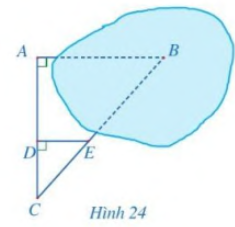
Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được \(AC = 50m,\,\,CD = 20m,\,\,DE = 18m\). Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?

Phương pháp:

Dựa vào hệ quả của định lý Thales để tính khoảng cách AB.

Lời giải:

Do DE ⊥ AC, AB ⊥ AC nên DE // AB.

Xét ∆ABC với DE // AB, ta có:

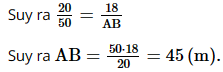
Bài 2 trang 61 SGK Toán 8 - Cánh Diều tập 2

Có thể gián tiếp đo chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?

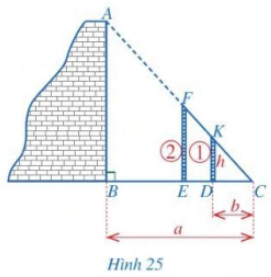
Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (Cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao \(DK = h\). Các khoảng cách \(BC = a,\,\,DC = b\) đo được bằng thước dây thông dụng.

a)      Em hãy cho biết người ta tiến hành đo đạc như thế nào?

b)     Tính chiều cao AB theo \(h,\,\,a,\,\,b\).

Phương pháp:

Dựa vào hệ quả của định lý Thales để tính khoảng cách AB.

Lời giải:

a) Cách tiến hành:

⦁ Vì cọc 2 di động được nên di chuyển cọc  sao cho cọc  trùng với AB, cụ thể F trùng với A, E trùng với B. 

⦁ Lúc này cọc  song song với AB. Do đó, ta có tỉ lệ giữa chiều cao của cọc  và AB bằng với tỉ lệ giữa khoảng cách DC và BC. Từ đó ta tính được chiều cao AB của bức tường thông qua hệ quả của định lí Thalès.

b) Xét ∆ABC với AB // KD (D ∈ BC, K ∈ AC), ta có:

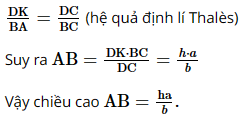
Bài 3 trang 61 SGK Toán 8 - Cánh Diều tập 2

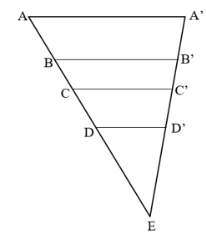
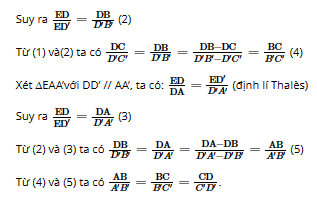
Trong hình 26, các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau. Không sử dụng thước đo, hãy giải thích vì sao độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A’B’, B’C’, C’D’.

Phương pháp:

Dựa vào kết quả từ bài tập 2 trang 57 Sách giáo khoa Toán 8 – Cánh diều.

Lời giải:

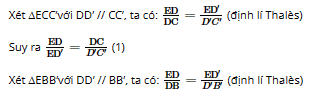
Bài 4 trang 61 SGK Toán 8 - Cánh Diều tập 2

Anh Thiện và chị Lương đứng ở hai phía bờ song và muốn ước lượng khoảng cách giữa hai vị trí A, B ở hai bên bờ sông (Hình 27).

-         Anh Thiện chọn vị trí C ở bên bờ sông sao cho A, B, C thẳng hàng và đo được BC=4m;

-         Tiếp theo, anh Thiện xác định vị trí D, chị Lương xác định vị trí E sao cho D, B, E thẳng hàng, đồng thời \(\widehat {BAE} = \widehat {BCD} = 90^\circ \);

-         Anh Thiện đo được CD=2m, chị Lương đo được AE=12m.

-         Hãy tính khoảng cách giữa hai vị trí A và B.

Phương pháp:

Dựa vào Hệ quả của định lý Thales để xác định khoảng cách AB.

Lời giải:

Ta có: AE ⊥ AC, CD ⊥ AC nên AE // CD.

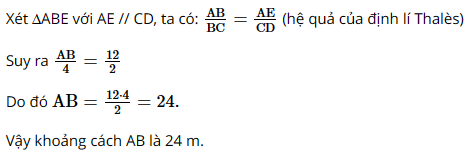
Sachbaitap.com