Giải SGK Toán 8 trang 115 Cánh Diều tập 1
Giải bài 1, 2, 3, 4, 5 trang 115 SGK Toán lớp 8 Cánh Diều tập 1. Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.
Bài 1 trang 115 SGK Toán 8 tập 1 - Cánh Diều
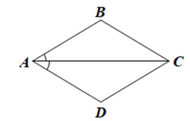
Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.
Phương pháp:
Áp dụng dấu hiệu nhận biết hình thoi: Hình bình hành có 2 cạnh kề bằng nhau là hình thoi
Lời giải:

Bài 2 trang 115 SGK Toán 8 tập 1 - Cánh Diều
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:
\(A{C^2} + B{{\rm{D}}^2} = 4\left( {O{A^2} + O{B^2}} \right) = 4{\rm{A}}{B^2}\)
Phương pháp:
Áp dụng định lí Pythagore trong các tam giác vuông để chứng minh.
Lời giải:
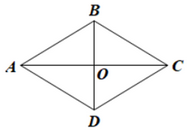
Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Do đó AC = 2OA, BD = 2OB.
Ta có: AC2 + BD2 = (2OA)2 + (2OB)2 = 4OA2 + 4OB2 = 4(OA2 + OB2).
Xét ΔOAB vuông tại O, theo định lí Pythagore ta có:
AB2 = OA2 + OB2
Suy ra AC2 + BD2 = 4(OA2 + OB2) = 4AB2.
Bài 3 trang 115 SGK Toán 8 tập 1 - Cánh Diều
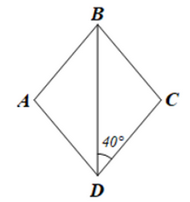
Cho hình thoi ABCD có \(\widehat {C{\rm{D}}B} = {40^o}\). Tính số đo mỗi góc của hình thoi ABCD.
Phương pháp:
Sử dụng tính chất của hình thoi.
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Lời giải:

Bài 4 trang 115 SGK Toán 8 tập 1 - Cánh Diều
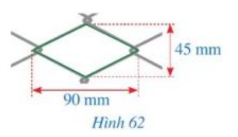
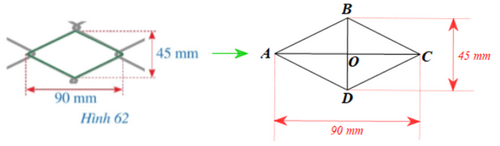
Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mmm và 90 mm. Độ dài cạnh của ô lưới mắt đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)?
Phương pháp:
Sử dụng tính chất của hình thoi
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Lời giải:

Bài 5 trang 115 SGK Toán 8 tập 1 - Cánh Diều
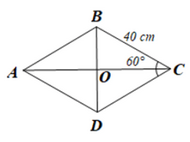
Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là \({60^o}\) (Hình 63).
Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm).

Phương pháp:
Sử dụng tính chất của hình thoi
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Lời giải:

Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 8
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài 9. Hình đồng dạng
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
