Giải SGK Toán 8 trang 120, 121 Cánh Diều tập 1
Giải bài 1, 2, 3, 4, 5, 6 trang 120, bài 7, 8, 8, 9, 10, 11, 12, 13 trang 121 SGK Toán lớp 8 Cánh Diều tập 1. Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây:
Xem thêm: Bài tập cuối Chương 5
Bài 1 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Cho tứ giác ABCD có \(\widehat A = {60^o},\widehat B = {70^o},\widehat C = {80^o}\). Khi đó, \(\widehat D\) bằng:
A. 130o
B. 140o
C. 150o
D. 160o
Phương pháp:
Áp dụng định lí: tổng các góc trong tứ giác bằng 360o
Lời giải:
ABCD là tứ giác nên:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\ \Rightarrow \widehat D = {360^o} - \widehat A - \widehat B - \widehat C = {360^o} - {60^o} - {70^o} - {80^o} = {150^o}\end{array}\)
Chọn đáp án C
Bài 2 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Cho hình thang cân ABCD có AB // CD, \(\widehat A = {80^o}\). Khi đó, \(\widehat C\) bằng:
A. 80o
B. 90o
C. 100o
D. 110o
Lời giải:
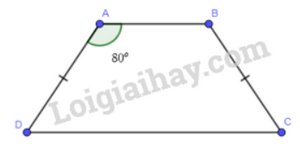
Vì ABCD là hình thang cân nên \(\widehat A = \widehat B = {80^o}\)
Khi đó: \(\widehat C = \widehat D = \frac{{{{360}^o} - \widehat B - \widehat A}}{2} = \frac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\left( {\widehat A + \widehat B + \widehat C + \widehat D = {{360}^o}} \right)\)
Chọn đáp án C
Bài 3 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Cho hình bình hành MNPQ có các góc khác 90o, MP cắt NQ tại I. Khi đó:
A. IM = IN
B. IM = IP
C. IM = IQ
D. IM = MP
Lời giải:
Hình bình hành MNPQ có các góc khác 90o, MP cắt NQ tại I. Khi đó: IM = IP; IN = IQ
Chọn đáp án B
Bài 4 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây:
A. NQ
B. MN
C. NP
D. QM
Lời giải:
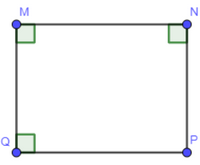
Vì MNPQ là hình chữ nhật nên MP = NQ vì hai hai đường chéo bằng nhau.
Chọn đáp án A.
Bài 5 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Hình 72 mô tả một cây cao 4m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây.
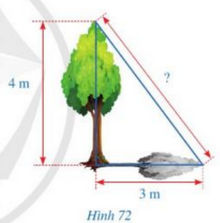
Lời giải:
Khoảng cách từ đỉnh xa nhất của bóng cây đến đỉnh của cây là cạnh huyền của một tam giác vuông.
Khi đó: Khoảng cách từ đỉnh xa nhất của bóng cây đến đỉnh của cây là: \(\sqrt {{3^2} + {4^2}} = 5m\)
Bài 6 trang 120 SGK Toán 8 tập 1 - Cánh Diều
Màn hình một chiếc ti vi có dạng hình chữ nhật với kích thước màn hình ti vi được tính bằng độ dài đường chéo của màn hình (đơn vị: inch, trong đó 1 inch = 2, 54m). Người ta đưa ra công thức tính khoảng cách an toàn khi xem ti vi để giúp khách hàng lựa chọn được chiếc ti vi phù hợp với căn phòng của mình như sau:
Khoảng cách tối thiểu = 5, 08 . d (cm)
Khoảng cách tối đa = 7, 62 . d (cm)
Trong đó, d là kích thước màn hình ti vi tính theo inch.
Với một chiếc ti vi có chiều dài màn hình 74, 7 cm, chiều rộng màn hình 32 cm;
a) Kích thước màn hình của ti vi đó là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?
b) Khoảng cách tối thiểu và khoảng cách tối đa để xem chiếc ti vi đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Lời giải:
a, Vì ti vi là hình chữ nhật nên đường chính là đường chéo của hình chữ nhật đó
Khi đó \({d^2} = \sqrt {74,{7^2} + {{32}^2}} \simeq 81(cm)\)
b, Khoảng cách tối thiểu là:
\(5,08.81 \approx 411,5(cm)\)
Khoảng cách tối đa là:
\(7,62.81 \approx 617,2(cm)\)
Bài 7 trang 121 SGK Toán 8 tập 1 - Cánh Diều
Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\). Chứng minh ABCD là hình bình hành.
Lời giải:
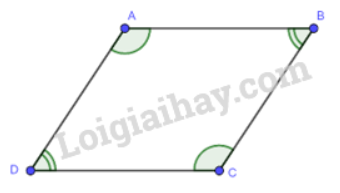
Xét \(\Delta ABD\)có: \(\widehat {BAD} + \widehat {ABD} + \widehat {BDA} = {180^0}\)
Xét \(\Delta BCD\)có: \(\widehat {BCD} + \widehat {ADC} + \widehat {DBC} = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BAD} + \widehat {ABD} + \widehat {BDA} = \widehat {BCD} + \widehat {ADC} + \widehat {DBC}\\ \Rightarrow \widehat {DAB} = \widehat {DBC}(do\,\widehat {BAD} = \widehat {BCD};\widehat {ABD} = \widehat {ADC})\end{array}\)
Xét \(\Delta ABD\)và \(\Delta CDB\)có:
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABD} = \widehat {CDB}\\BDchung\\\widehat {DBA} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta ABD = \Delta CDB(g.c.g)\\ \Rightarrow AB = DC\\AD = CB\end{array}\)
Suy ra tứ giác ABCD là hình bình hành vì có cặp cạnh đối bằng nhau
Bài 8 trang 121 SGK Toán 8 tập 1 - Cánh Diều
Cho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.
Lời giải:
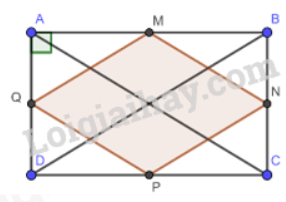
Vì ABCD là hình chữ nhật nên AB = CD; AD = BC
Vì M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD. DA nên:
AQ = BN = CN = DQ
AM = BM = CP = DP
Xét 4 tam giác AQM, BNM, CNP. DQP có:
AQ = BN = CN = DQ
AM = BM = CP = DP
Suy ra:
\(\begin{array}{l}\Delta AQM = \Delta BNM = \Delta CNP = \Delta DQP\\ \Rightarrow QM = MN = NP = QP\end{array}\)
Vậy tứ giác MNPQ có QM = MN = NP = QP nên tứ giác MNPQ là hình thoi.
Bài 9 trang 121 SGK Toán 8 tập 1 - Cánh Diều
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Lời giải:
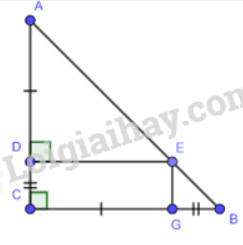
Vì \(\Delta ABC\)vuông cân tại C.
\( \Rightarrow \widehat {C{\rm{AD}}} = {45^0} \Rightarrow \widehat {DA{\rm{E}}} = {45^0}\)
Vì \(\Delta ADE\)vuông cân tại D.
\( \Rightarrow \widehat {DA{\rm{E}}} = {45^0} \Rightarrow \widehat {DE{\rm{A}}} = {45^0} \Rightarrow \Delta ADE\)là tam giác vuông cân tại D
Suy ra AD = DE (1)
Mà: AD = CG (2)
Từ (1), (2) suy ra: DE = CG.
Mặt khác DE//CG (vì cùng vuông góc với AC)
Suy ra tứ giác CDEG là hình bình hành
Mặt khác: \(\widehat {DCG} = {90^0}\)
Suy ra hình bình hành CDEG là hình chữ nhật
Bài 10 trang 121 SGK Toán 8 tập 1 - Cánh Diều
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Lời giải:
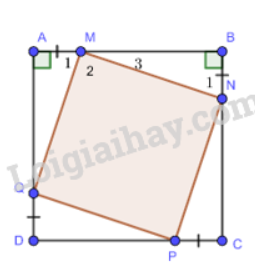
Ta có: \(\Delta AMG = \Delta BNM = \Delta CPN = \Delta AQC\)(hai cạnh góc vuông)
Suy ra MQ = NM = PN = QC
Suy ra MNPQ là hình thoi
Do: \(\Delta AMQ = \Delta BNM \Rightarrow {\widehat M_1} = \widehat {BNM}\) (2 góc tương ứng)
Mà: \(\widehat {BNM} + {\widehat M_3} = {90^0}\)(do \(\Delta BNM\)vuông tại B)
\( \Rightarrow {\widehat M_1} + {\widehat M_3} = {90^0} \Rightarrow {\widehat M_2} = {180^0} - {\widehat M_1} - {\widehat M_3} = {180^0} - {90^0} = {90^0}\)
Vậy hình thoi MNPQ có một góc bằng 90o nên MNPQ là hình vuông
Bài 11 trang 121 SGK Toán 8 tập 1 - Cánh Diều
Cho bình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a) \(\Delta IAM = \Delta ICN\)
b) Tứ giác AMCN là hình bình hành.
c) Ba điểm B, I, D thẳng hàng.
Lời giải:
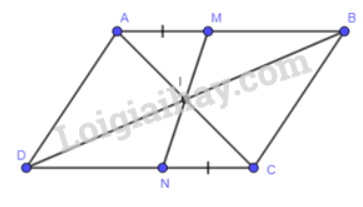
a) Xét tam giác IAM ta có: \(\widehat {AMI} + \widehat {MIA} + \widehat {MAI} = {180^o}\)
Xét tam giác ICN có: \(\widehat {CNI} + \widehat {NIC} + \widehat {NCI} = {180^o}\)
Vì: \(\widehat {MIA} = \widehat {NIC}\) (đối đỉnh)
\(\widehat {MAI} = \widehat {NCI}\) (fo AB // CD)
Suy ra: \(\widehat {AMI} = \widehat {CNI}\)
Xét tam giác IAM và tam giác ICN có:
\(\widehat {AMI} = \widehat {CNI}\)
AM = CN
\(\widehat {MIA} = \widehat {NIC}\)
\( \Rightarrow \Delta IAM = \Delta ICN(g - c - g)\)
b) Vì \(\Delta IAM = \Delta ICN \Rightarrow MC = AN\)
Xét tứ giác AMCN có: MC = AN; AM = CN
Suy ra tứ giác AMCN là hình bình hành.
c) Vì tứ giác AMCN là hình bình hành
Suy ra I là trung điểm của AC
Suy ra I là trung điểm của BD (vì ABCD là hình bình hành)
Suy ra ba điểm B, I, D thẳng hàng.
Bài 12 trang 121 SGK Toán 8 tập 1 - Cánh Diều
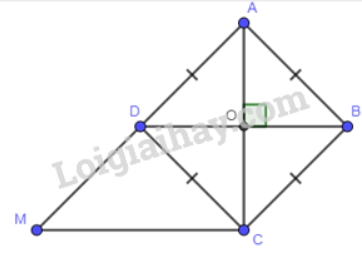
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a) \(O{\rm{D}} = \frac{1}{2}CM\) và tam giác ACM là tam giác vuông.
b) Ba điểm A, D, M thẳng hàng.
c) Tam giác DCM là tam giác cân
Lời giải:
a) Vì BCMD là hình bình hành
Suy ra: BD = CM (1)
Mà ABCD là hình thoi
O là giao điểm của AC và BD
\( \Rightarrow O{\rm{D}} = \frac{1}{2}B{\rm{D}}(2)\)
Từ (1) và (2) suy ra: \(O{\rm{D}} = \frac{1}{2}CM\)
Vì BCND là hình bình hành nên BD // CM (3)
Vì ABCD là hình thoi nên \(B{\rm{D}} \bot AC(4)\)
Từ (3), (4) suy ra: \(AC \bot CM\)
Suy ra: tam giác ACM là tam giác vuông tại C
b) ta có: AD // BC (vì ABCD là hình thoi)
DM // BC (vì DBCM là hình bình hành)
Suy ra A, D, M thẳng hàng
c) Ta có:BC = DC (vì ABCD là hình thoi)
DM = BC (vì DBCM là hình bình hành)
Suy ra: DM = DC
Suy ra tam giác DCM là tam giác cân tại D
Bài 13 trang 121 SGK Toán 8 tập 1 - Cánh Diều
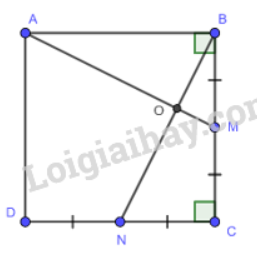
Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, Cd. Gọi O là gao điểm của AM và BN. Chứng minh:
a) \(\Delta ABM = \Delta BCN\)
b) \(\widehat {BAO} = \widehat {MBO}\)
c) \(AM \bot BN\)
Lời giải:
a) Vì ANCD là hình vuông
suy ra: AB = BC = CD = DA
Gọi M là trung điểm của các cạnh BC, CD
Suy ra: BM = MC = CN = CD
Xét hai tam giác vuông ABM và BCN có:
AB = BC
BM = CN
\( \Rightarrow \Delta ABM = \Delta BCN\) (hai cạnh góc vuông)
b) theo câu a: \(\Delta ABM = \Delta BCN\)
\(\begin{array}{l} \Rightarrow \widehat {BAM} = \widehat {CBN}\\ \Rightarrow \widehat {BAO} = \widehat {MBO}\end{array}\)
c) Vì \(\Delta ABM = \Delta BCN\)
\(\begin{array}{l} \Rightarrow \widehat {MAB} = \widehat {NBM}\\ \Rightarrow \widehat {MAB} = \widehat {OBM}\end{array}\)
Mà: \(\widehat {MAB} + \widehat {{M_1}} = {90^o}\) (do tam giác ABM vuông tại M)
\( \Rightarrow \widehat {OBM} + \widehat {{M_1}} = {90^o}\)
Xét tam giác OBM có:
\(\begin{array}{l}\widehat {BOM} + \widehat {OBM} + \widehat {{M_1}} = {180^o}\\ \Rightarrow \widehat {BOM} + {90^o} = {180^o}\\ \Rightarrow \widehat {BOM} = {180^o} - {90^o} = {90^o}\end{array}\)
Suy ra: tam giác OBM vuông tại O
\(\begin{array}{l} \Rightarrow BO \bot OM\\ \Rightarrow BN \bot AM\end{array}\)
Sachbaitap.com
Bài viết liên quan
- Bài tập cuối chương 8
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài 9. Hình đồng dạng
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!