Giải SGK Toán 8 trang 40, 41 Chân trời sáng tạo tập 1

A. Trắc Nghiệm

Bài 1 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Biểu thức nào sau đây không phải là đa thức

A. \(\sqrt 2 {x^2}y\)              

B. \( - \dfrac{1}{2}x{y^2} + 1\)                    

C. \(\dfrac{1}{{2z}}x + y\)                 

D. 0

Phương pháp:

Sử dụng khái niệm đa thức: Đa thức là một đơn thức hoặc một tổng của hai hay nhiều đơn thức.

Lời giải:

Bài 2 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Đơn thức nào sau đây đồng dạng với đơn thức \( - 2{x^3}y\)?

A. \(\dfrac{1}{3}{x^2}yx\)                 

B. \(2{x^3}yz\)           

C. \( - 2{x^3}z\)                     

D. \(3x{y^3}\)

Phương pháp:

Thu gọn các đơn thức để tìm đơn thức đồng dạng với đơn thức \( - 2{x^3}y\)

Lời giải:

Bài 3 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Biểu thức nào sau đây không phải là đa thức bậc 4?

A. \(2{x^2}yz\)                       

B. \({x^4} - \dfrac{1}{3}{x^3}{y^2}\)                      

C. \({x^2}y + xyzt\)               

D. \({x^4} - {2^5}\)

Phương pháp:

Dựa vào khái niệm bậc của đa thức: Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó

Lời giải:

Bài 4 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Biểu thức nào sau đây không phải là phân thức?

A. \({x^2}y + y\)                    

B. \(\dfrac{{3xy}}{{\sqrt 2 z}}\)                   

C. \(\dfrac{{\sqrt x }}{2}\)                            

D. \(\dfrac{{a + b}}{{a - b}}\)                      

Phương pháp:

Sử dụng khái niệm phân thức: Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng \(\dfrac{{A}}{{B}}\)  , trong đó A,B là những đa thức và B khác 0

Lời giải:

Bài 5 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Kết quả của phép nhân \((x + y - 1)(x + y + 1)\) là:

A. \({x^2} - 2xy + {y^2} + 1\)

B. \({x^2} + 2xy + {y^2} - 1\)

C. \({x^2} - 2xy + {y^2} - 1\)

D. \({x^2} + 2xy + {y^2} + 1\)

Phương pháp:

Sử dụng quy tắc nhân đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau. 

Lời giải:

Đáp án đúng là: B

Ta có: (x + y – 1)(x + y + 1)

        = (x + y)² – 1²

        = x² + 2xy + y² – 1.

Bài 6 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Kết quả của phép nhân \((2x + 1)(4{x^2} - 2x + 1)\) là:

A. \(8{x^3} - 1\)                     

B. \(4{x^3} + 1\)                    

C. \(8{x^3} + 1\)                    

D. \(2{x^2} + 1\)

Phương pháp:

Sử dụng quy tắc nhân đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Lời giải:

Đáp án đúng là: C

Ta có: (2x + 1)(4x² – 2x + 1)

        = (2x + 1)[(2x)² – 2x.1 + 1²]

        = (2x)³ + 1³

        = 8x³ + 1.

Bài 7 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Khi phân tích đa thức \(P = {x^4} - 4{x^2}\) thành nhân tử thì được:

A. \(P = {x^2}(x - 2)(x + 2)\)   

B. \(P = x(x - 2)(x + 2)\)

C. \(P = {x^2}(x - 4)(x + 4)\)  

D. \(P = x(x - 4)(x + 2)\)

Phương pháp:

Sử dụng phương pháp đặt nhân tử chung, dùng hẳng đẳng thức

- Đặt nhân tử chung ra ngoài.

- Sử dụng hằng đẳng thức \({a^2}-{b^2}=(a-b)(a+b)\)

Lời giải:

Đáp án đúng là: A

Ta có: P = x⁴ – 4x²

              = (x²)² – (2x)²

              = (x² + 2x)(x² – 2x)

              = x(x + 2).x(x – 2)

              = x²(x – 2)(x + 2).

Bài 8 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Kết quả của phép trừ \(\dfrac{2}{{{{(x + 1)}^2}}} - \dfrac{1}{{{x^2} - 1}}\) là:

A. \(\dfrac{{3 - x}}{{(x - 1){{(x + 1)}^2}}}\)

B. \(\dfrac{{x - 3}}{{(x - 1){{(x + 1)}^2}}}\)

C. \(\dfrac{{x - 3}}{{{{(x + 1)}^2}}}\)

D. \(\dfrac{1}{{(x - 1){{(x + 1)}^2}}}\)   

Phương pháp:

Sử dụng quy tắc trừ phân thức: Muốn trừ phân thức \( \dfrac{A}{B}\) cho phân thức \( \dfrac{C}{D}\), ta cộng \( \dfrac{A}{B}\) với phân thức đối của \( \dfrac{C}{D}\)

Lời giải:

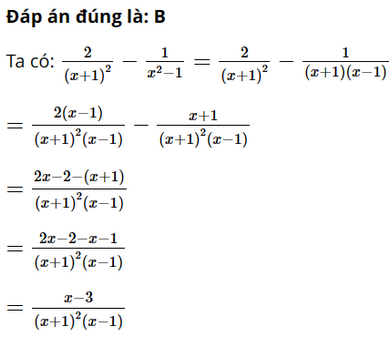
Bài 9 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Khi phân tích đa thức \(R = 4{x^2} - 4xy + {y^2}\) thành nhân tử thì được:

A. \(R = {(x + 2y)^2}\)   

B. \(R = {(x - 2y)^2}\)

C. \(R = {(2x + y)^2}\) 

D. \(R = {(2x - y)^2}\)

Phương pháp:

Sử dụng phương pháp hằng đẳng thức

Lời giải:

Đáp án đúng là: D

Ta có R = 4x² – 4xy + y²

             = (2x)² – 2.2x.y + y²

             = (2x – y)².

Bài 10 trang 40 SGK Toán 8 tập 1 - Chân trời sáng tạo

Khi phân tích đa thức \(S = {x^6} - 8\) thành nhân tử thì được:

A. \(S = \left( {{x^2} + 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)

B. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)

C. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)

D. \(S = \left( {x - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)

Phương pháp:

Sử dụng phương pháp hằng đẳng thức

Lời giải:

Đáp án đúng là: C

Ta có: S = x⁶ – 8

              = (x²)³ – 2³

              = (x² – 2)[(x²)² + x².2 + 2²]

              = (x² – 2)(x⁴ + 2x² + 4).

B. Tự Luận

Bài 11 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Tính giá trị của đa thức \(P = x{y^2}z - 2{x^2}y{z^2} + 3yz + 1\) khi \(x = 1\); \(y =  - 1\); \(z = 2\)

Phương pháp:

Thay các giá trị vào đa thức rồi tính

Lời giải:

Thay x = 1, y = –1 và z = 2 vào đa thức P ta được:

P = 1.(–1)².2 – 2.1².(–1).2² + 3.(–1).2 + 1

   = 2 + 8 – 6 + 1

   = 5.

Vậy P = 5 khi x = 1, y = –1, z = 2.

Bài 12 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho đa thức \(P = 3{x^2}y - 2x{y^2} - 4xy + 2\).

a) Tìm đa thức \(Q\) sao cho \(Q - P =  - 2{x^3}y + 7{x^2}y + 3xy\)

b) Tìm đa thức \(M\) sao cho \(P + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\)

Phương pháp:

a) Thay đa thức P vào để tìm đa thức Q

b) Thay đa thức P vào để tìm đa thức M

Lời giải:

a) Ta có: Q – P = –2x³y + 7x²y + 3xy.

Suy ra Q = P + (–2x³y + 7x²y + 3xy)

               = 3x²y – 2xy² – 4xy + 2 –2x³y + 7x²y + 3xy

               = (3x²y + 7x²y) – 2xy² + (– 4xy + 3xy) + 2 –2x³y

               = 10x²y – 2xy² – xy + 2 –2x³y.

Vậy Q = 10x²y – 2xy² – xy + 2 –2x³y.

b) Ta có: P + M = 3x²y² – 5x²y + 8xy.

Suy ra M = 3x²y² – 5x²y + 8xy – P

                = 3x²y² – 5x²y + 8xy – (3x²y – 2xy² – 4xy + 2)

                = 3x²y² – 5x²y + 8xy – 3x²y + 2xy² + 4xy – 2

                = 3x²y² + (– 5x²y – 3x²y) + (8xy + 4xy) + 2xy² – 2

                = 3x²y² –8x²y + 12xy + 2xy² – 2.

Vậy M = 3x²y² –8x²y + 12xy + 2xy² – 2.

Bài 13 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính sau:

a) \({x^2}y\left( {5xy - 2{x^2}y - {y^2}} \right)\)

b) \(\left( {x - 2y} \right)\left( {2{x^3} + 4xy} \right)\)

Phương pháp:

Sử dụng quy tắc nhân đa thức

Lời giải:

a) x²y(5xy – 2x²y – y²)

= x²y.5xy – x²y.2x²y  – x²y.y²

= 5x³y² – 2x⁴y² – x²y³.

b) (x – 2y)(2x² + 4xy)

= x(2x² + 4xy) – 2y.(2x² + 4xy)

= 2x³ + 4x²y – 4x²y – 8xy²

= 2x³ – 8xy².

Bài 14 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính sau:

a) \(18{x^4}{y^3}:12{\left( { - x} \right)^3}y\)

b) \({x^2}{y^2} - 2x{y^3}:\left( {\dfrac{1}{2}x{y^2}} \right)\)

Phương pháp:

Thực hiện phép chia đa thức

Lời giải:

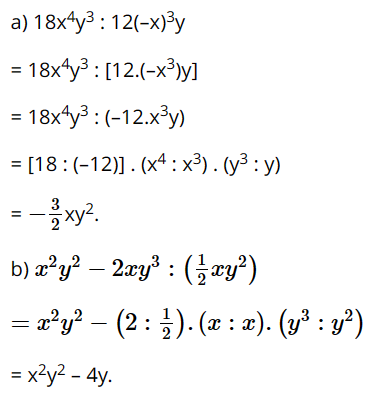
Bài 15 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Tính:

a) \(\left( {2x + 5} \right)\left( {2x - 5} \right) - \left( {2x + 3} \right)\left( {3x - 2} \right)\)

b) \({\left( {2x - 1} \right)^2} - 4\left( {x - 2} \right)\left( {x + 2} \right)\)

Phương pháp:

Thực hiện phép nhân đa thức, khai triển hằng đẳng thức

Lời giải:

a) \(\left( {2x + 5} \right)\left( {2x - 5} \right) - \left( {2x + 3} \right)\left( {3x - 2} \right)\)        

\(\begin{array}{l} = \left( {4{x^2} - 25} \right) - \left( {6{x^2} - 4x + 9x - 6} \right)\\ = 4{x^2} - 25 - 6{x^2} + 4x - 9x + 6\\ =  - 2{x^2} - 5x - 19\end{array}\)

b) \({\left( {2x - 1} \right)^2} - 4\left( {x - 2} \right)\left( {x + 2} \right)\)

\(\begin{array}{l} = \left( {4{x^2} - 4x + 1} \right) - 4\left( {{x^2} - 4} \right)\\ = 4{x^2} - 4x + 1 - 4{x^2} + 16\end{array}\)

\( =  - 4x + 17\)

Bài 16 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \({\left( {x - 1} \right)^2} - 4\) 

b) \(4{x^2} + 12x + 9\) 

c) \({x^3} - 8{y^6}\)

d) \({x^5} - {x^3} - {x^2} + 1\) 

e) \( - 4{x^3} + 4{x^2} + x - 1\) 

f) \(8{x^3} + 12{x^2} + 6x + 1\)

Phương pháp:

Sử dụng các phương pháp hằng đẳng thức, nhóm hạng tử

Lời giải:

a) (x – 1)² – 4

= (x – 1)² – 2²

= (x – 1 + 2)(x – 1 – 2)

= (x + 1)(x – 3).

b) 4x² + 12x + 9

= (2x²) + 2.2x.3 + 3²

= (2x + 3)².

c) x³ – 8y⁶

= x³ – (2y²)³

= (x³ – 2y²)[(x³)² + x³.2y² + (2y²)²]

= (x³ – 2y²)(x⁶ + 2x³y² + 4y⁴).

d) x⁵ – x³ – x² + 1

= (x⁵ – x³) – (x² – 1)

= x³(x² – 1) – (x² – 1)

= (x² – 1)(x³ – 1)

= (x + 1)(x – 1).(x – 1).(x² + x + 1)

= (x + 1)(x – 1)²(x² + x + 1).

e) –4x³ + 4x² + x – 1

= (–4x³ + 4x²) + (x – 1)

= –4x²(x – 1) + (x – 1)

= (x – 1)(–4x² + 1)

= (x – 1)[1² – (2x)²]

= (x – 1)(1 + 2x)(1 – 2x).

g) 8x³ + 12x² + 6x + 1

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³

= (2x + 1)³.

Bài 17 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

 Cho \(x + y = 3\) và \(xy = 2\). Tính \({x^3} + {y^3}\)

Phương pháp:

Sử dụng khai triển hằng đẳng thức tổng hai lập phương rồi tính giá trị của đa thức

Lời giải:

Ta có: x³ + y³

= (x + y)(x² – xy + y²)

= (x + y)[(x² + 2xy + y²) – 3xy]

= (x + y)[(x² + 2xy + y²) – 3xy]

= (x + y)[(x + y)² – 3xy]

Thay x + y = 3 và xy = 2 vào đa thức trên ta có:

x³ + y³ = 3.(3² – 3.2) = 3.(9 – 6) = 3.3 = 9.

Bài 18 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính sau:

a) \(\dfrac{{2{x^2} - 1}}{{x - 2}} + \dfrac{{ - {x^2} - 3}}{{x - 2}}\)                       

b) \(\dfrac{x}{{x + y}} + \dfrac{y}{{x - y}}\)    

c) \(\dfrac{1}{{x - 1}} - \dfrac{2}{{{x^2} - 1}}\)

d) \(\dfrac{{x + 2}}{{{x^2} + xy}} - \dfrac{{y - 2}}{{xy + {y^2}}}\)                                  

e) \(\dfrac{1}{{2{x^2} - 3x}} - \dfrac{1}{{4{x^2} - 9}}\)                     

g) \(\dfrac{{2x}}{{9 - {x^2}}} + \dfrac{1}{{x - 3}} - \dfrac{1}{{x + 3}}\)      

Phương pháp:

Sử dụng quy tắc cộng, trừ phân thức

Lời giải:

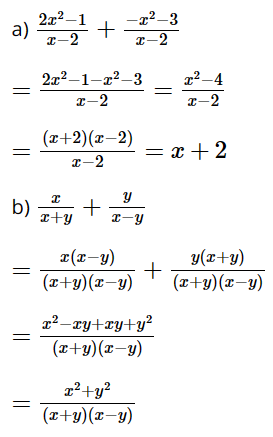
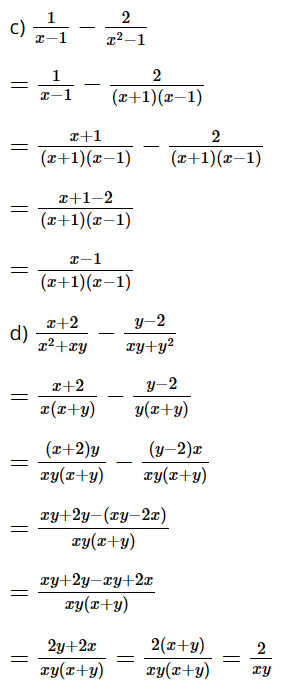
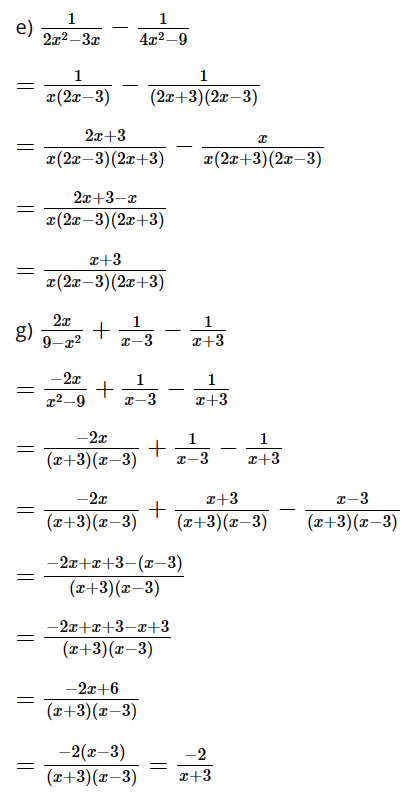
Bài 19 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Thực hiện các phép tính sau:

a) \(\dfrac{{8y}}{{3{x^2}}} \cdot \dfrac{{9{x^2}}}{{4{y^2}}}\)

b) \(\dfrac{{3x + {x^2}}}{{{x^2} + x + 1}} \cdot \dfrac{{3{x^3} - 3}}{{x + 3}}\)

c) \(\dfrac{{2{x^2} + 4}}{{x - 3}} \cdot \dfrac{{3x + 1}}{{x - 1}}:\dfrac{{{x^2} + 2}}{{6 - 2x}}\)

d) \(\dfrac{{2{x^2}}}{{3{y^3}}}:\left( { - \dfrac{{4{x^3}}}{{21{y^2}}}} \right)\)

e) \(\dfrac{{2x + 10}}{{{x^3} - 64}}:\dfrac{{{{\left( {x + 5} \right)}^2}}}{{2x - 8}}\)

f) \(\dfrac{1}{{x + y}}\left( {\dfrac{{x + y}}{{xy}} - x - y} \right) - \dfrac{1}{{{x^2}}}:\dfrac{y}{x}\)      

Phương pháp:

Sử dụng quy tắc nhân, chia đa thức, thứ tự thực hiện phép tính

Lời giải:

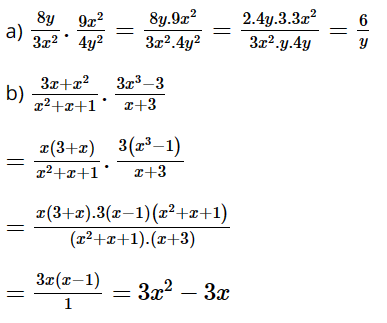
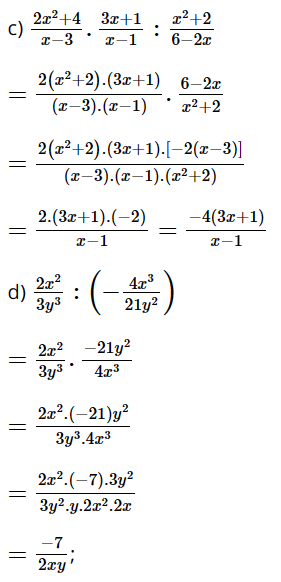
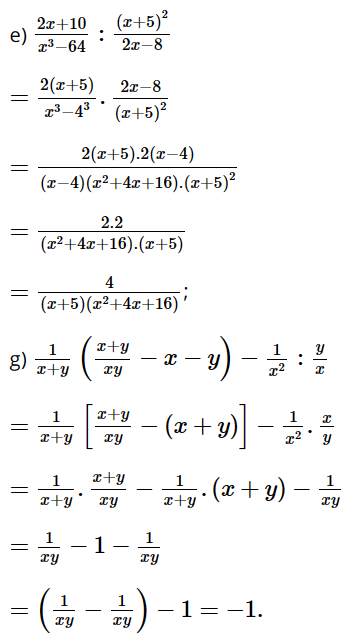
Bài 20 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Hôm qua thanh long được bán với giá \(a\) đồng mỗi ki-lô-gam. Hôm nay, người ta đã giảm giá \(1000\) đồng cho mỗi ki-lô-gam thanh long. Với cùng số tiền \(b\) đồng thì hôm nay mua được nhiều hơn bao nhiêu ki-lô-gam thanh long so với hôm qua?

Phương pháp:

Tính giá thanh long sau khi giảm

Tính số kg thanh long mua được hôm nay

Tính số kg thanh long mua được nhiều hơn so với hôm qua

Lời giải:

Bài 21 trang 41 SGK Toán 8 tập 1 - Chân trời sáng tạo

Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ \(x + 3\) km/h và đi ngược dòng với tốc độ \(x - 3\) km/h (\(x > 3)\).

a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường thuyền đã đi. Lúc này thuyền cách bến A bao xa?

b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A \(15\)km, nghỉ \(30\) phút, rồi quay về bến A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A?

Phương pháp:

a) Sử dụng công thức tính quãng đường

b) Sử dụng công thức tính thời gian

Lời giải:

a) Quãng đường thuyền đi xuôi dòng là: \(x(x + 3) = {x^2} + 3x\) (km)

Quãng đường thuyền đi ngược dòng là: \(2(x - 3) = 2x - 6\) (km)

Quãng đường thuyền đã đi là: \({x^2} + 3x + 2x - 6 = {x^2} + 5x - 6\) (km)

Lúc này thuyền các bến A số km là: \(({x^2} + 3x) - (2x - 6) = {x^2} + x + 6\) (km)

b) Thời gian thuyền đi xuôi dòng là: \(\dfrac{{15}}{{x + 3}}\) (giờ)

Thời gian thuyền đi ngược dòng là: \(\dfrac{{15}}{{x - 3}}\) (giờ)

Vì khi đến B thuyền nghỉ 30 phút \( = \dfrac{1}{2}\) giờ nên thuyền về A lúc số giờ là:

\(\begin{array}{l}\dfrac{{15}}{{x + 3}} + \dfrac{{15}}{{x - 3}} + \dfrac{1}{2}\\ = \dfrac{{15.2.\left( {x - 3} \right)}}{{2\left( {x + 3} \right)\left( {x - 3} \right)}} + \dfrac{{15.2\left( {x + 3} \right)}}{{2\left( {x + 3} \right)\left( {x - 3} \right)}} + \dfrac{{{x^2} - 9}}{{2\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \dfrac{{30x - 90 + 30x + 90 + {x^2} - 9}}{{2\left( {x + 3} \right)\left( {x - 3} \right)}}\\ = \dfrac{{{x^2} + 60x - 9}}{{2\left( {{x^2} - 9} \right)}}\end{array}\)    

Sachbaitap.com